В.В.Калашников, Г.В.Носовский, А.Т.Фоменко
ЗВЕЗДЫ СВИДЕТЕЛЬСТВУЮТ.
Астрономический анализ хронологии.
Датировка Альмагеста Птолемея. Коперник, Тихо Браге и "античный" Гиппарх.

Том 3 , книга 1

Глава 7.
ДАТИРОВКА ЗВЕЗДНОГО КАТАЛОГА АЛЬМАГЕСТА.
СТАТИСТИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ МЕТОДЫ.

5. ДАТИРОВКА КАТАЛОГА АЛЬМАГЕСТА ПО МНОЖЕСТВУ 8-ЗВЕЗДНЫХ КОНФИГУРАЦИЙ, СОСТОЯЩИХ ИЗ ЯРКИХ ЗВЕЗД.

Идея данного расчета, как и сам расчет, принадлежит сотруднику государственного университета штата Флорида (США), известному специалисту в области анализа данных, профессору Деннису Дьюку (Dennis Duke, Florida State Univ.). Мы встретились с ним в 1999 году, в г.Торонто (Канада), на конференции, организованной для обсуждения наших результатов об Альмагесте. Деннис Дьюк заинтересовался проблемой датировки Альмагеста и провел собственный анализ.

Он предложил рассмотреть совокупность всех конфигураций из восьми ярких звезд Альмагеста. В качестве ярких звезд профессор Деннис Дьюк взял множество из 72 звезд, величина которых в Альмагесте меньше 3. Напомним, что чем меньше величина, тем ярче звезда. Из этого множества 72 звезд были выбраны все сочетания по 8 звезд, для которых максимальная ошибка в широте в каталоге Альмагеста не превосходит 10' на некотором ненулевом временн'ом интервале (t₁,t₂), целиком лежащем от 400 года до н.э. до 1600 года н.э. Всего получилось 736 сочетаний по 8 звезд из примерно 500 тысяч возможных сочетаний. Каждое такое сочетание задает свой интервал датировки (t₁,t₂). Деннис Дьюк рассмотрел множество центров этих "датирующих интервалов", то есть множество величин 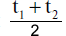. Оказалось, что если построить гистограмму частот распределения этих центров на оси времени, то возникает ярко выраженный максимум на отрезке 600-900 годов н.э., см. рис.7.24. Следовательно, наиболее вероятной датой составления каталога Альмагеста являются VII--X века н.э.

Подход, предложенный профессором Д.Дьюком, обладает тем преимуществом, что плохо измеренные или слишком медленно меняющиеся звездные конфигурации автоматически исключаются из выборки. Дело в том, что для них интервалы датировки при 10-минутном уровне по широте либо пусты, либо настолько велики, что не умещаются внутри выбранного профессором Д.Дьюком априорного исторического интервала от 400 года до н.э. до 1500 года н.э. Оказывается, что после такого довольно жесткого отбора остается все еще много конфигураций, а именно, 736 восьми-звездных конфигураций. Если взять в качестве датировки по некоторой такой конфигурации центр ее "датирующего интервала" по уровню 10' в широте, то мы получим дату для каталога Альмагеста с некоторой случайной ошибкой, то есть, возмущенную дату составления каталога. Построив распределение возмущенных дат, мы сможем существенно точнее, чем по отдельной конфигурации, датировать каталог Альмагеста.

Естественно предположить, что истинная датировка каталога служит средним значением для случайно возмущенных дат. Это среднее можно оценить по имеющемуся в нашем распоряжении эмпирическому распределению. Считая, что истинное распределение возмущений близко к нормальному, легко оценить его дисперсию. Выборочное среднеквадратичное отклонение для распределения на рис.7.24 равно приблизительно 350 лет. Ввиду того, что выборка была цензурирована по априорному интервалу времени, который оказался несимметричным относительно центра распределения, см. рис.7.24, оценка среднего по данному распределению оказывается смещенной. Если учесть этот эффект, то более аккуратная оценка для среднеквадратичного отклонения будет еще меньше.

Далее, центр выборочного распределения лежит около 800 года. Если бы элементы выборки были независимы, то можно было бы сделать вывод о том, что истинная дата составления каталога Альмагеста лежит в пределах 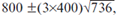то есть в пределах 800 ± 45 лет. На самом деле элементы выборки независимыми считать нельзя, поэтому реальная точность датировки каталога Альмагеста 800-м годом н.э. существенно ниже, чем ± 45 лет. Тем не менее, датировку началом н.э. и более ранними эпохами в этой ситуации можно считать крайне маловероятной, практически исключенной.

 

6. АНАЛИЗ УСТОЙЧИВОСТИ СТАТИСТИЧЕСКОЙ ПРОЦЕДУРЫ ДАТИРОВКИ КАТАЛОГА АЛЬМАГЕСТА.

6.1. НЕОБХОДИМОСТЬ ВАРИАЦИИ ВЕЛИЧИН, УЧАСТВУЮЩИХ В АЛГОРИТМЕ.

При описанной выше процедуре датировки, некоторые величины, определяющие алгоритм, были выбраны достаточно произвольно, а другие явились результатом статистических выводов. Поэтому необходимо проверить, как ведет себя получаемый интервал датировки при вариации указанных величин.

 

6.2. ВАРИАЦИЯ УРОВНЯ ДОВЕРИЯ.

Величина ε, определяющая уровень доверия, выбиралась нами достаточно произвольно. Напомним, что в статистических задачах она имеет смысл допустимой вероятности ошибки, то есть если, например, ε=0,1, то мы допускаем ошибку с вероятностью 0,1. Чем меньше ε, тем шире доверительный интервал. Зависимость величины доверительного интервала от ε рассмотрена в главах 5 и 6. См., в частности, табл.6.3.

Рассмотрим, как изменяется полученный нами интервал датировки в зависимости от ε. Мы уже отмечали, -- и это следует из рис.7.11, -- что при всех значениях ε, не б'ольших 0,1, интервал датировки каталога Альмагеста получается один и тот же. Это утверждение является следствием расположения интервалов S_t(α) при α=10'.

Но, быть может, если выбрать другое значение гарантированной точности α каталога Альмагеста, не равное 10 минутам, заявленным Птолемеем, то картина окажется другой? Выберем α=15'. См. соответствующую заштрихованную область на рис.7.11. Естественно, при этом интервал возможных датировок каталога Альмагеста расширится. Верхняя граница расширенного интервала датировки вновь не зависит от ε и равна t=3, то есть, 1600 год н.э. Нижняя граница весьма слабо зависит от ε, а именно, при ε=0,1 она равна t=16,3, то есть 270 год н.э., а при ε=0,005 имеем t=16,5, то есть 250 год н.э.

Таким образом, эти результаты показывают, что СУБЪЕКТИВНЫЙ ВЫБОР УРОВНЯ ДОВЕРИЯ ε ПРАКТИЧЕСКИ НЕ ВЛИЯЕТ НА ЗНАЧЕНИЕ НИЖНЕЙ ГРАНИЦЫ ИНТЕРВАЛА ВОЗМОЖНЫХ ДАТИРОВОК КАТАЛОГА АЛЬМАГЕСТА.

Попутно мы выяснили, как влияет на размер интервала датировок величина α. Смысл которой -- точность измерения широт именных звезд каталога, а именно, даже при увеличении α с 10' (точность, заявленная Птолемеем) до 15', то есть при увеличении в 1,5 раза, получаемый интервал датировок каталога Альмагеста не захватывает скалигеровскую эпоху Птолемея, не говоря уже о скалигеровской эпохе Гиппарха.

 

6.3. СОКРАЩЕНИЕ СОСТАВА ИНФОРМАТИВНОГО ЯДРА ЗВЕЗДНОГО КАТАЛОГА АЛЬМАГЕСТА.

В известной мере субъективным является и выбор информативного ядра каталога. В самом деле, из 12 именных звезд мы отсеяли четыре -- Канопус, Превиндемиатрикс, Сириус и Аквилу = Альтаир. Если отсев первых двух звезд объясняется причинами, "внешними" для нашего исследования, то Сириус и Аквилу мы не рассматривали по той причине, что групповые ошибки их окружений не совпадают с групповой ошибкой для Zod A. Но в главе 6 показано, что есть еще по крайней мере две звезды -- Лира и Капелла - групповые ошибки окружений которых могут не совпадать с групповой ошибкой для Zod A. Условность предыдущего предположения вызвана тем, что достоверно определить эти ошибки не представляется возможным. К тому же эти две звезды находятся далеко от Зодиака и близко к относительно плохо измеренной области неба М.

Итак, посмотрим, какой интервал возможных датировок каталога Альмагеста получится, если исключить указанные две звезды и оставить в информативном ядре каталога лишь шесть звезд: Арктур, Регул, Антарес, Спику, Аселли, Процион. рис.7.25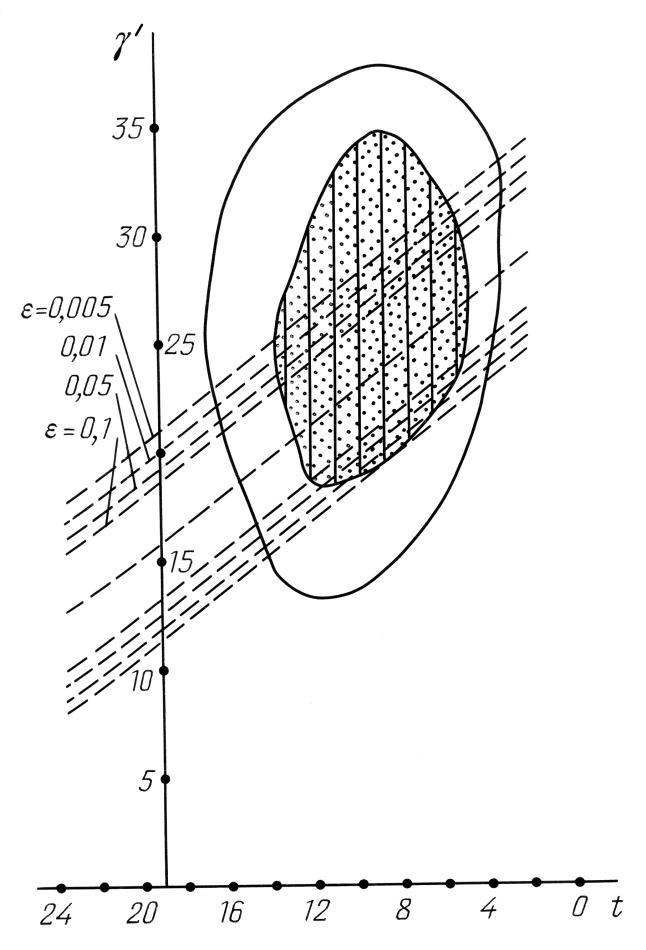, аналогичный рис.7.11, показывает -- что' при этом произойдет. Хотя область значений параметра γ, при котором максимальная широтная невязка не превосходит уровня 10' или 15', сильно расширилась, границы интервала возможных датировок изменились незначительно, а именно, верхние границы, -- и для 10-минутного и для 15-минутного уровней, -- сохранились прежними. Нижняя граница для 15-минутного уровня также не изменилась по сравнению с полученной при рассмотрении 8 звезд ядра каталога. Нижняя же граница для α=10' сдвинулась в прошлое не более чем на 100 лет.

Тем самым, если принимать во внимание лишь 6 именных звезд каталога Альмагеста, лежащих в области Zod A, либо в ее непосредственной окрестности, то можно заключить, что звездный каталог Альмагеста не мог быть составлен ранее 500 года н.э.

 

6.4. ЕСЛИ ОТБРОСИТЬ АРКТУР, ДАТИРОВКА КАТАЛОГА АЛЬМАГЕСТА СУЩЕСТВЕННО НЕ МЕНЯЕТСЯ.

Возникает еще один вопрос. Не является ли полученный нами интервал датировки каталога Альмагеста следствием движения всего лишь одной звезды? Этот вопрос резонный, так как если такая звезда найдется, то возможная неточность в измерении ее координат может исказить получаемую датировку. Единственным кандидатом на подобную роль "датирующей звезды" в информативном ядре является Арктур. Это самая быстрая из восьми звезд, во многом определяющая наш интервал датировки. Ее окружение к тому же измерено не очень хорошо, см. главу 6. Поэтому, если по какой-либо причине индивидуальная ошибка координат Арктура велика, то, вообще говоря, интервал возможных датировок может сильно исказиться. Проверим, каким станет этот интервал, если из информативного ядра каталога Альмагеста УДАЛИТЬ АРКТУР и оставить в нем лишь 7 звезд. Разумеется, длина нового интервала возрастет. Она, грубо говоря, обратно пропорциональна максимальной скорости звезд из информативного ядра каталога. рис.7.26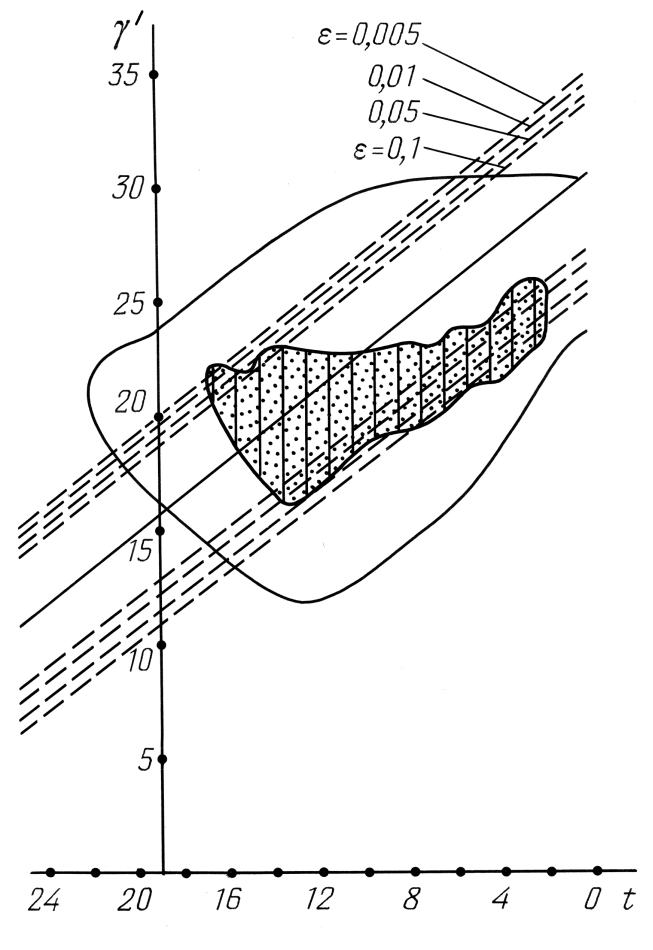 иллюстрирует получающуюся при этом картину. Из рисунка ясно видно, что даже в отсутствие самой быстрой звезды информативного ядра, -- Арктура -- 10-минутная область не опускается ниже 300 года н.э. (t=16) при уровне доверия 1 - ε = 0,95 или ниже. И лишь если мы поднимем уровень доверия до 1- ε = 0,99, -- то есть до 99%, -- эта область начинает захватывать 200 год н.э, то есть даже при 99%-ном уровне доверия скалигеровская эпоха Птолемея не захватывается интервалом датировки. Тем более не захватывается еще более древняя скалигеровская эпоха Гиппарха.

Рассмотрим теперь 15-минутную область. Она достигает 100 года до н.э. (t=20) при уровне доверия 1 − ε = 0,95. При уровне доверия 1 − ε = 0,99 достигается 200 год до н.э., то есть лишь при таком сильном "расшатывании условий" захватывается скалигеровская эпоха Птолемея.

Возникает вопрос: достаточен ли в нашем случае уровень доверия 1 − ε = 0,95 для 10-минутной области? По-видимому -- да. Уровень 95% определяет достаточно высокую для исторических исследований точность. Фактически такая величина характерна даже для технических приложений, где требования к точности очень высоки. Для справки скажем, что в работе [273], посвященной датировке Альмагеста, взято значение ε=0,2, то есть уровень доверия выбран всего лишь 80%. Таким образом, полученные нами выводы обладают очень высокой степенью достоверности.

Подводя итоги, можно заключить, что ни изменение уровня доверия, ни изменение состава информативного ядра, ни вариация значения гарантированной точности измерений не меняют основного сделанного вывода: звездный каталог Альмагеста составлен существенно позже скалигеровской эпохи Птолемея, то есть позже I--II веков н.э.

 

7. ГЕОМЕТРИЧЕСКАЯ ДАТИРОВКА КАТАЛОГА АЛЬМАГЕСТА.

Выводы, полученные в разделах 2--6, имели статистический характер. Сами значения групповых ошибок определялись с некоторой статистической погрешностью. Поэтому выводы о совпадении групповых ошибок в различных созвездиях каталога Альмагеста также, вообще говоря, могли быть ложными, хотя и с весьма малыми вероятностями. Устойчивость полученных статистических результатов проанализирована в предыдущем разделе. Но чтобы полностью гарантировать себя от возможных статистических ошибок, теперь мы полностью откажемся от статистики и перейдем к чисто геометрическим рассуждениям.

Рассмотрим "минимаксную широтную невязку" для определенного ранее информативного ядра каталога Альмагеста, состоящего из 8 именных звезд:

δ(t) = min Δ(t, γ, φ),

(7.7.1)

 

где минимум берется по всевозможным значениям γ и φ. Сравним данное равенство с равенством (7.3.1). Отличие между ними -- лишь в области изменения параметра γ. В формуле (7.3.1) γ изменялось в пределах доверительного интервала, накрывающего точку γ_stat(t). Равенство (7.7.1) такого ограничения не содержит. Следовательно, δ(t) ≤ Δ(t).

Обозначим через γ_geom(t) и φ_geom(t) значения (γ,φ), доставляющие минимум правой части (7.7.1). Возможная неточность процедуры нахождения γ_geom(t) и φ_geom(t) для нас здесь будет совершенно несущественна.

Вспомним ситуацию, которая уже встретилась нам в разделе 3. Там мы сняли ограничения с параметра φ. Ограничения накладывались лишь на γ. Как мы видели, это привело к интервалу датировки, на который статистические характеристики оценки для φ никак не влияют. Хотя, конечно, величина этого интервала получилась достаточно большой. Нечто подобное будет проделано нами здесь по отношению к обоим параметрам (γ,φ). Введенные выше величины γ_geom(t) и φ_geom(t) можно, если угодно, считать параметрами, задающими групповую ошибку для информативного ядра каталога. При условии, что каталог составлен в некую эпоху t.

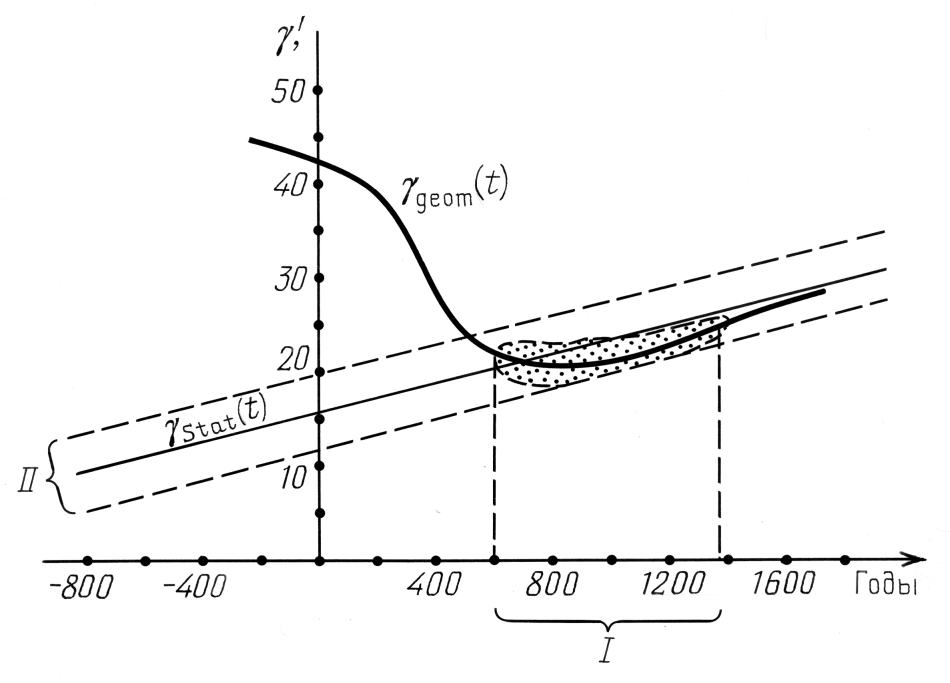На основе всего сказанного выше, будем считать интервалом возможной датировки каталога совокупность таких моментов времени t, для которых δ(t) ≤ 10'. Чтобы найти этот интервал, изобразим на рис.7.27, рис.7.28, рис.7.29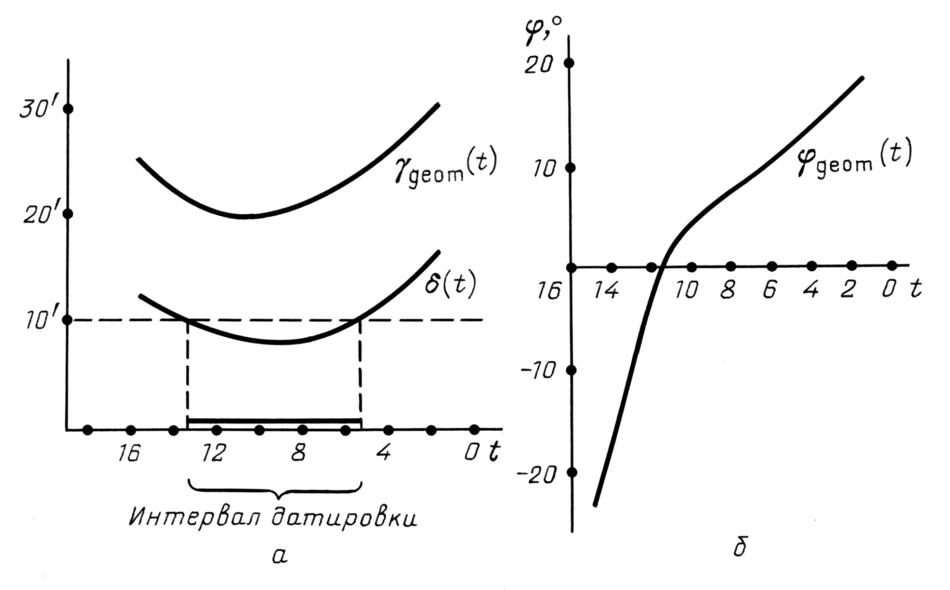 и рис.7.30 график δ(t), а также графики функций γ_geom(t) и φ_geom(t). Приведенный график δ(t) построен с помощью равенства (7.7.1), в котором величины Δ(t,γ, φ) вычислялись по формуле (7.3.1) и производился перебор по γ и φ. На рис.7.28 для сравнения показан график зависимости γ_geom(t) вместе с доверительной полосой. См. раздел 6. Показана также область таких значений (t, γ), что Δ(t, γ, φ) < 10' при некотором φ.

Из приведенных графиков следует, что найденный ранее интервал датировок каталога Альмагеста не расширяется, даже если применить геометрическую процедуру датировки. Это, в частности, дополнительно подтверждает, что наши статистические оценки γ_stat^{Zod A}, рассчитанные по б'ольшей части звезд каталога Альмагеста, действительно соответствуют групповой ошибке в небольшой совокупности именных звезд Альмагеста. Кроме того, доказано, что вне временн'ого интервала от 600 года н.э. до 1300 года н.э. не существует такого способа совмещения реального звездного неба и звездного неба Альмагеста, при котором все звезды из его информативного ядра имели бы широтную невязку не более 10'.

В заключение приведем также графики зависимости от предполагаемой датировки t индивидуальных широтных невязок для 8 звезд информативного ядра Альмагеста при фиксированных значениях γ = 20' и φ = 0. См. рис.7.31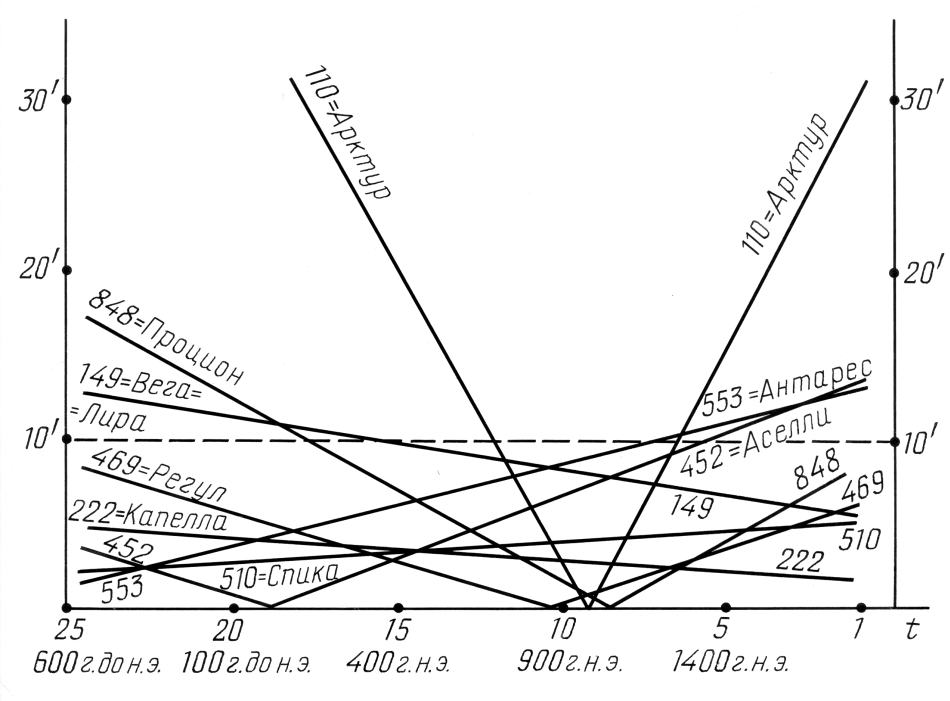. Верхняя огибающая этих графиков близка к кривой на рис.7.25, изображающей зависимость минимальной невязки от предполагаемой датировки t для большей части временн'ого интервала после 0 года н.э. (0<t<19). Это связано с тем, что значение γ = 20' близко к γ_geom(t), а φ = 0 близко к φ_geom(t) для большей части этого интервала. К изменению φ картина мало чувствительна.

Pис.7.31 показывает -- на каких именно звездах информативного ядра каталога Альмагеста достигается минимаксное значение широтной невязки δ(t) при различных предполагаемых датировках t. На рис.7.31 четко выделяется скопление нулевых значений широтных невязок около значения t=10, то есть около 900 года н.э. При таком значении предполагаемой датировки каталога практически обнуляются невязки сразу для трех звезд информативного ядра, а именно, для Арктура (α Boo), Регула (α Leo) и Проциона (α CMi). Для остальных звезд информативного ядра каталога Альмагеста широтная невязка обращается в нуль только у Аселли (γ Can) около начала нашей эры.

Любопытно сопоставить отмеченный факт скопления нулевых невязок с тем, что Арктур и Регул, наряду с Сириусом, занимали исключительное положение в "древней" астрономии. Так, Арктур -- самая яркая звезда северного полушария -- являлся, по-видимому, первой звездой, получившей в "древне"-греческой астрономии собственное имя. Оно упоминается уже в описании звездного неба, данном в поэтической форме в "древней" поэме Арата. Регул -- это звезда, служившая в греческой астрономии отправной точкой для измерения координат всех остальных звезд и планет.