BÖLÜM 2:
ASTRONOMİK TARİHLEMELER
1. D’’ PARAMETRESİNİN AY HAREKETİ TEORİSİNDEKİ MUAMMALI SIÇRAYIŞI
Ay hareketi teorisine dayanarak [534] her tutulma için tarihin, ay gölgesinin geçme hattının, fazın vb. hesaplandığı etkili tablolar (kurallar) oluşturulmuştur. Mesela F.K. Ginzel’in ünlü astronomi kuralına bakınız [1154]. Eski bir belgede bir tutulma oldukça ayrıntılı bir şekilde tasvir edilmişse, metinden bu tutulmanın faz, gölgenin geçme hattı vs. gibi gözlemlenmiş nitelikleri öğrenilebilir. Bu nitelikleri tablolardan alınan belirlenmiş niteliklerle kıyaslayarak, kuraldan uygun bir tutulmayı, yani nitelikleri benzer olan tutulmayı bulmaya çalışabiliriz. Bunu başarabilirsek ilgilendiğimiz olayı tarihleyebiliriz. Mamafih, vakayinamedeki tarife astronomik kuraldaki bir değil birkaç tutulmanın uyması söz konusu olabilir. Bu durumda, tarihlemenin birkaç versiyonu olur. Bugün hem “antik” kaynaklarda hem de Orta Çağ kaynaklarında tarif edilen bütün tutulmalar az çok bu yöntem yardımıyla tarihlenmiştir [1154], [1155], [1156], [1315], [1316], [1317] vs.
Bugün “eski” tutulmaların tarihlenmesi bazı astronomik araştırmalarda kullanılmaktadır. Mesela Ay hareketi teorisinde, ivmeyi niteleyen, Ay uzanımının ikinci türevi olan D’’ parametresi denilen kavram yer almaktadır. Uzanımın ne olduğunu hatırlatalım. Res.2.1’de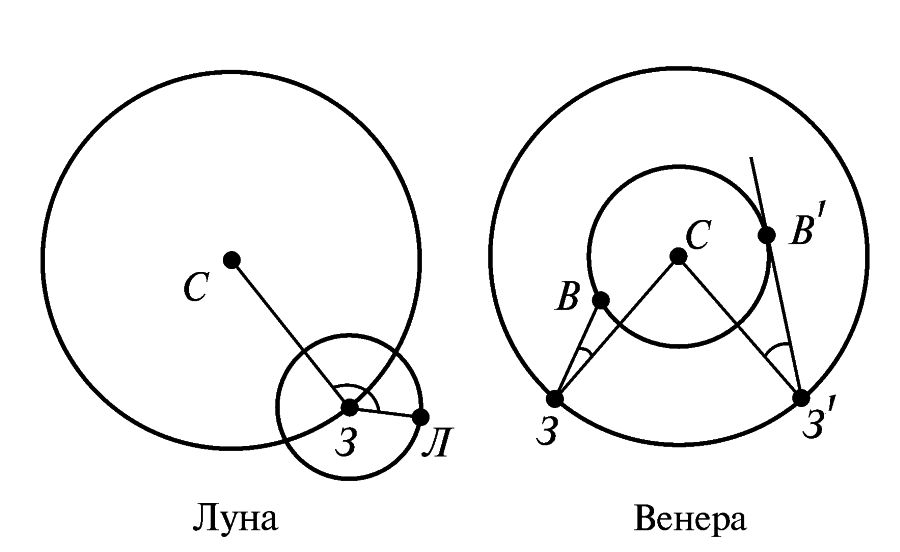 Dünya’nın Güneş etrafındaki yörüngesi ve Ay’ın Dünya etrafındaki yörüngesi gösterilmiştir. “3C” ile “3Л” vektörleri arasındaki açıya Ay uzanımı (moon elongation) denir. Yani, Ay uzanımı Dünya’dan Güneş’e ve Ay’a geçen görüş ışınları arasındaki açıdır. Bu, herhalde zamana bağlıdır. Resimde sağda, mesela Venüs’ün uzanımı gösterilmiştir. Dünya’dan Venüs’e geçen З'В' görüş ışınının Venüs’ün yörüngesine dokunduğu açıya azami uzanım denir. Res.2.1
Dünya’nın Güneş etrafındaki yörüngesi ve Ay’ın Dünya etrafındaki yörüngesi gösterilmiştir. “3C” ile “3Л” vektörleri arasındaki açıya Ay uzanımı (moon elongation) denir. Yani, Ay uzanımı Dünya’dan Güneş’e ve Ay’a geçen görüş ışınları arasındaki açıdır. Bu, herhalde zamana bağlıdır. Resimde sağda, mesela Venüs’ün uzanımı gösterilmiştir. Dünya’dan Venüs’e geçen З'В' görüş ışınının Venüs’ün yörüngesine dokunduğu açıya azami uzanım denir. Res.2.1 ’deki yörüngelerin, dairesel olarak gösterildiği halde gerçekte eliptik olduğunu kaydetmek gerekiyor. Ancak eksantriklik çok yüksek olmadığı için elipsler burada kolaylık sağlamak amacıyla daire şeklinde gösterilmiştir.
’deki yörüngelerin, dairesel olarak gösterildiği halde gerçekte eliptik olduğunu kaydetmek gerekiyor. Ancak eksantriklik çok yüksek olmadığı için elipsler burada kolaylık sağlamak amacıyla daire şeklinde gösterilmiştir.
Bazı astronomik bilgisayar problemleri için Ay ivmesinin geçmişteki hareketlerini bilmek faydalıdır. Zamanın fonksiyonu olan D’’nin büyük zaman aralığında hesaplanması sorunu 1972 yılında Londra Kraliyet Topluluğu ve Britanya Bilimler Akademisi tarafından düzenlenmiş olan toplantıda tartışılmıştı [1453]. D’’ parametresinin hesaplanmasının temeline aşağıdaki şema konulmuştu. Ay hareketi denklemindeki D’’ parametresi dâhil olmak üzere parametreleri hesaplamak için, bunların çağdaş değerleri alınıp Eski Çağ tutulmalarının teorik olarak hesaplanmış olan niteliklerinin, tarihlenmiş olan tutulmaların eski belgelerde verilen niteliklerine daha net uyması şeklinde çeşitlendirilir. D’’ parametresi tutulmaların tarihleri hesaplanırken göz ardı edilir. Bunun sebebi, hesaplanması için Ay ivmesinin kesin değerinin bilinmesinin gerekmediği tutulma tarihinin daha kaba bir parametre olmasıdır. Ay ivmesinin değişimi tutulmanın daha detaylı niteliklerini etkilemektedir, mesela tutulma hattını, yani Ay’ın gölgesinin tutulma sırasında yeryüzünde çizdiği çizgiyi bir tarafa doğru oynatabilmektedir.
Ünlü Amerikalı astronom Robert Newton D’’nin zamana bağlı olduğunu hesaplamıştır [1303]. Fikrine göre, D’’ parametresi, “tarihleri (-700) yılından şimdiki zamana kadar uzanan aralıktan geçen çok sayıda verinin yardımıyla iyi bir şekilde saptanabilir” [1304], s.113. Robert Newton “eski” tutulmaların gözlemlerine dayanarak D’’ parametresinin 12 muhtemel değerini hesaplamıştır. Skaliger kronolojisine tümüyle güvendiği için, R. Newton’un tutulmaların tarihlerini Skaliger kronoloji cetvellerinden alması anlaşılıyor. 1627-1860 yılları arasındaki teleskopik Ay gözlemlerini araştıran Martin’in sonuçları ile birleştirilmiş olan R. Newton’un sonuçları D’’nin deneysel zaman bağlılığı eğrisinin çizilmesine yol açmıştır. Bu eğri Res.2.2’de gösterilmiştir.
gösterilmiştir.
R. Newton şunu yazmıştı: “(M.S. - A.F.) 700 yılından yaklaşık 1300 yılına kadar... D’’nin pek hızlı düşmesi en ŞAŞIRTICI olan olaydır... Bu düşüş “kare dalganın” D’’nin dokunum değerinde var olduğu anlamına gelmektedir... D’’nin hareketinde bu büyüklükteki değişimleri çağdaş jeofizik teorilerine dayanarak AÇIKLAMAK MÜMKÜN DEĞİLDİR” [1304], s.114; [1453]. R. Newton’un “Dünya-Ay Sistemi’ndeki Çekim Gücü Olmayan Güçler İle İlgili Astronomik Kanıtlar” çalışması [1303] da bu muammalı aralığın, D’’nin davranışındaki 10 katlık sıçrayışının (yani D’’nin davranışı 10 kat değiştiği zaman) anlatılması denemelerine dairdir. Robert Newton’un var olduğunu düşünmek zorunda kaldığı bu esrarengiz “çekim gücü olmayan güçlerin” BİR ŞEKİLDE BİR YERDE KENDİNİ GÖSTERMEDİĞİNİ kaydetmemiz gerek.
R. Newton çizilmiş olan cetveli araştırırken “(-700) yılından (+500) yılına kadar D’’ değerlerinin son 1000 yıl içinde her anda var olan aynı D''nin değerlerine kıyasla olası en düşük değer olduğunu” belirtmek zorunda kalmıştı [1304], s.114.
Sonra ise R. Newton şunu yazmıştı: “Çağdaş verilerle kombine edilmiş olan bu değerlendirmeler, hem D’’nin şaşılacak kadar büyük değerlerinin olabildiğini hem de son
2000 yıl boyunca BÜYÜK ve ANİ DEĞİŞİMLERE uğradığını göstermektedir. Yaklaşık 800 yılında D'' işaretini bile değiştirmişti.” [1453], s.115.
Sonuç:
1) Güya M.S. V. yüzyılda, D’’ değerinin birden düşmesi, üstelik 10 kat düşmesi, sıçrayışı başlıyor.
2) XI. yüzyıldan itibaren sonraki zaman içerisinde, D’’ parametresinin değerleri az çok sabittir ve çağdaş değerine daha yakındır.
3) D’’ değerlerinin güya V-XI. yüzyıllar arasındaki aralıkta büyük bir dağılımı görünmektedir.
Yeni Kronoloji’de bu esrarengiz olgunun doğal bir açıklamasının olduğunu görüyoruz.
2. “ANTİK ÇAĞ” VE ORTA ÇAĞ TUTULMALARI DOĞRU TARİHLENMİŞLER MİYDİ?
2.1. Bazı Astronomi Bilgileri
Aşağıda bu bölümü daha iyi anlamaya yardım edecek kısa bir bilgi bülteni sunalım. Daha ayrıntılı bilgiler için mesela [534]’e bakınız.
Ay Dünya’nın etrafında hareket ederken Dünya’daki yer konisinin gölgesine düşer, daha doğrusu Ay’a dönen gece yarıküresine Ay tutulması gelir. Bu, Dünya’nın gece yarıküresinin her noktasından gözlemlenebilir. Tutulma üç saatten fazla sürmez. Tutulmanın sadece dolunay sırasında ortaya çıkması mümkündür ancak Ay’ın hareketindeki kuralsızlıklardan dolayı her dolunayda gerçekleşmez. Ay tutulmalarının yineleme aralığı kabaca ve genel olarak periyodiktir. Buna Saros Döngüsü denir. Bir Saros Döngüsü yaklaşık
18 yıldır. Bu süre içinde aşağı yukarı 28 Ay tutulması gerçekleşir, dolayısıyla hemen hemen verili her yılın yanında en az bir Ay tutulmasının bulunması mümkündür. Bir Saros, 50-60 yıllık sistematik gözlemler sonucunda kolayca bulunabilir, dolayısıyla astronomi gelişiminin şafağında biliniyor olabilirdi. Saros’a göre Ay tutulmalarının tahmini yine de pek güvenilir değildir. Bunun sebebi ise sadece Saros’un yanlışlığı değil, tutulmanın, yeryüzünün verilen noktasında gündüz olduğundan Ay’ın görünmediği anda yer alabilmesidir.
Güneş tutulması, gözlemci Ay gölgesinin konisinde olduğunda gerçekleşir. Ay Güneş kursunu tümüyle kapadığı takdirde gözlemin yapıldığı yere karanlık basar ve yıldızlar görünür olur. Bu tam tutulmadır. Gözlemin yapıldığı yere göre hesaplandığında, tam güneş tutulmasının ekvator bölgesindeki süresi en fazla 8 dakika, orta bölgedeki süresi ise en fazla 6
dakikadır. Ay’ın gölgesi dar bir hat çizerek Dünya yüzeyinden saniyede yüz on metre hızla hareket eder. Bu hattın genişliği 4 dereceyi aşmaz. Mutlak gölgenin hattı yarı gölgenin hattı ile zıhlanmıştır. Bu arada, yarı gölgenin genişliği mutlak gölge hattının ortasından (tutulma ekseninden) bir tarafa, orta bölgede yaklaşık 30 dereceye denk gelirken, ekvator bölgesinde ise yaklaşık 15 derecedir. Gözlemci, yarı gölgenin hattında, Ay’ın sadece bir kısmını kapattığı Güneş kursunu görür. Buna kısmi tutulma denir. Güneş kursunun azami derecede Ay ile kapanmasına tutulma derinliği ya da evre denir. Evre, genellikle b değeri ile değerlendirilmektedir. b değeri b=12h formülüne göre hesaplanır. Bu arada h değeri, Güneş’in çapının Ay ile kaplanan kısmının çapın tümüne bölünmesiyle hesaplanır. Dolayısıyla tam Güneş tutulması 12 puanlık evreye sahiptir. Gözümüz Güneş tutulmasını 3''-
4'' puanlık fazdan başlayarak kursun kararması olarak tespit eder.
Ay tutulmasının evreleri biraz farklı bir şekilde hesaplanır, bu yöntem de şudur: Tutulma tam olmaktan ileri olduğu takdirde, tutulmanın sürekliliğiyle doğru orantılı olan bir sayı tam tutulmanın 12’’ evresine eklenir. Böylelikle Ay tutulmasının evresi 22,7’ye kadar ulaşabilir.
Güneş tutulmalarında, bazen, tam Ay gölgesinin konisinin Dünya’ya ulaşmadığı durumlarla karşı karşıya kalırız. Bu durumda, halka biçimindeki Güneş tutulmasının ortaya çıkması mümkündür. Böyle bir tutulma sırasında, her kısmi tutulma sırasında olduğu gibi, yıldızlar görünmez. Güneş tutulmasının sadece yeniay sırasında olması mümkündür. Ancak Güneş tutulması her yeniaya refakat etmez, çünkü Dünya, Ay yörüngesinin ekliptiğe (yani Dünya yörüngesinin yüzeyine) doğru eğilmesinden dolayı Ay gölgesinin konisinin yanından kayıverebilir. Dünya’nın her bölgesinde belli bir tarihten önce ya da sonra 10-20 yıl içinde ortalama en az 6 puanlık evreli bir Güneş tutulması ortaya çıkar.
Güneş tutulmalarının tahmini, birçok başka tedirginlikle belirlenen Ay hareketinin karmaşıklığından dolayı çetinleşmektedir. Güneş tutulmaları, 15 kısmi, 14 halka biçimli, 2 tam halka biçimli ve 12 tam tutulma olmak üzere yaklaşık 43 Güneş tutulmasını içeren
Saros’a göre tahmin edilmeye çalışılabilir. Ancak Saros’taki bu tutulmalar Dünya’nın farklı bölgelerinde yer alır. Dolayısıyla bir bölge için yapılan tahmin ortalama 400 olayda bir kez doğru çıkar. Yani kabaca değerlendirirsek, Saros temelindeki doğru tahminin olasılığı
1/400’dür [544], 4.cilt, s.415. Teorik bakımdan, süresi 24 yıl olan Üç Katlı Saros en iyi sonuçları vermelidir. Ancak onun yardımıyla yapılan tahminin olasılığı yaklaşık 1/99 olduğu için o da pratik olarak kullanılamaz. Astronominin tarihi bakımından, ampirik Üç Katlı Saros Güneş tutulmalarının sadece uzun süreli gözlemleri sayesinde keşfedilebilir. Üç Katlı Saros ile ayrılmış olan Güneş tutulmalarının oldukça az sayıda tekerrüründen dolayı bu keşif, (bilinmeyen periyodisiteyi belirlemek için gereken matematiksel işlemlerin çetinlikleri bir yana) ancak doğa bilimleri gelişmişse mümkündür.
Ortaya çıktığı gibi, Güneş tutulmalarının az çok güvenilir tahmininin sadece, en az temel eşitsizlikleri göz önünde bulunduran, oldukça gelişmiş Ay hareketi kuramına dayanarak yapılması mümkündür. Bu yüzden, N. Kopernik’ten yüz yıl sonra bile Güneş tutulmalarının
tahminlerini yapmayı bilmezlerdi. Dolayısıyla, XVI-XVII. yüzyıllardan önceki bütün Güneş tutulmalarının tahminlerine yönelik bildirileri son derecede dikkatli hatta şüpheci bir şekilde ele almamız gerekir.
2.2. İlginç Bir Efekt Bulunmuştur: Nesnel Astronomik Tarihleme “Eski Çağ” Tutulmalarının Tarihlerini Orta Çağ’a Atıyor
1973 yılında, güya D’’ parametresindeki sıçrayıştan ibaret olan efekt, bkz. [1303], ile N.A. Morozov’un [544] Eski Çağ tutulmalarının tarihlenmesine yönelik sonuçları arasında olası bir bağlılığın olması bu kitabın 70’li yılların başlangıcında gök mekaniği ile ilgili sorunlarla uğraşan yazarının dikkatini çekmişti. Bu sorunun araştırılması ve D’’
parametresinin yeniden hesaplanması, D’’ için elde edilen yeni eğrinin nitelikçe bambaşka bir şekil aldığını göstermişti. Bu arada ESRARENGİZ SIÇRAYIŞ TÜMÜYLE ORTADAN KALKMIŞTI. D’’ parametresinin gerçekten çağdaş değeriyle uyuşan aynı sabit değerin civarında dalgalanmakta olduğu görünmekteydi. Bkz. A.T. Fomenko’nun yazıları [1128], [883]. Bu sonucun özü kısaca aşağıda ifade edilmiştir.
D’’ parametresinin eski hesaplamasının temelinde Skaliger kronolojisine göre kabul edilmiş olan Eski Çağ tutulmalarının tarihleri vardır. Astronomların D’’nin esrarengiz sıçrayışının açıklanmasına yönelik bütün teşebbüsleri, bugün “antik” ve Orta Çağ sayılan tutulmaların tarihlerinin doğru saptanıp saptanmadığı sorusuna değinmemişti. Başka deyişle, vakayinamede tarif edilmiş olan tutulma parametreleri ile Skaliger kronolojisinin bu vakayinamede tarif edildiğini kabul etmeyi önerdiği gerçek tutulmanın hesaplanmış olan parametreleri birbirine ne kadar kesin uymaktadır?
[544]’de nesnel astronomik tarihlemenin şu yöntemleri önerilmektedir: Araştırılmakta olan vakayinameden, içinde tarif edilen evre, zaman, gözlemin coğrafi konumu vb. dâhil olmak üzere bütün tutulma nitelemeleri alınır. Sonra ise bu nitelemelere sahip olan bütün tutulmaların tarihleri etkili astronomik tablolarda mekanik olarak art arda yazılır. N.A. Morozov [544]’de, artık ortaya çıkmış olan Skaliger kronolojisinin baskısı altında olan astronomların tutulmayı (hem de vakayinameyi) tarihliyorken sonuçta elde ettikleri bütün tarihleri değil sadece Skaliger kronolojisi tarafından araştırılmakta olan tutulmaya ve ilgili olaylara önceden tahsis edilmiş olan zaman aralığına düşen tarihleri araştırmak zorunda kaldıklarını meydana çıkarmıştı.
Bu da, ortaya çıktığı gibi, astronomların, vakayinamenin tariflerine uygun düşen, “istenen” yüzyıla ait olan tutulmayı bulamamalarına yol açmıştı. Sonuçta, astronomlar Skaliger kronolojisinden şüphe etmemiş, bunun yerine çarpıtmalara başvurmak zorunda kalmışlardı. Mesela, sadece bazı ayrıntıları vakayinamenin tariflerine uygun düşen tutulmayı göstermişlerdi. N.A. Morozov “antik” sayılan tarihlemelerin denetlemesini yaptıktan sonra, bu tutulmalarla ilgili bildirilerin aşağıdaki iki kategoriye ayrıldığını meydana çıkarmıştı.
1- Ayrıntıları içermeyen kısa, bulanık bildiriler. Çoğu örnekte, tarif edilen olayın bir tutulma olup olmadığı belli değildir. Bu kategorideki astronomik tarihlemenin ya hiç anlamı yoktur ya da o kadar çok çeşitli çözümü var ki bunlar tarihin hemen hemen her dönemine uyabilir.
2- Ayrıntıları içeren bildiriler. Burada çoğu kez ya tek anlamlı astronomik çözüm ya da en fazla iki-üç çözüm var.
Nesnel astronomik tarihleme gerçekleştirilirken ayrıntılı, iyi bir şekilde tarif edilmiş olan bütün tutulmaların, M.Ö. 1000 yılından M.S. 500 yılına kadar zaman aralığında bulunan Skaliger tarihine değil, çok daha geç tarihlere (bazen yüzlerce yıl) ait olduğu ortaya çıkmıştır. Üstelik bütün bu yeni çözümler M.S. 500 ile 1700 yılları arasındaki aralığa denk düşmektedir. Buna rağmen, N.A. Morozov Skaliger kronolojisinin M.S. 300 ile 1800 yılları arasındaki aralıkta esas itibariyle doğru olduğunu düşünüp burada aykırılıkların ortaya çıkmadığını kabul ettiği için, M.S. 500-1700 yıllarına ait olan tutulmaları araştırmamıştır. Buna daha ayrıntılı bir şekilde bakalım.
N.A. Morozov’un kararlılığı, Skaliger kronolojisinin M.S. XIII-XIV. yüzyıllar dönemine kadar doğru olmadığını anlamak için yeterli olmamıştı. Skaliger-Petavius kronolojisinin genelde doğru olduğunu düşündüğü için M.S. IV. yüzyılda durmuştu. Onun bu yanlış düşüncesi Eski Çağ tutulmalarının analizini kaçınılmaz bir biçimde etkilemişti. Morozov’un araştırması, şimdi anladığımız gibi, pek nesnel olmamıştı. N.A. Morozov IV-VI. yüzyıllardan sonraki kronolojiye açıktan açığa dokunmak istememişti. Bu anlaşılabilir. Herhalde binlerce yıla suni olarak uzatılmış olan Skaliger kronolojisinden, sadece M.S. XI. yüzyıldan itibaren başlayan kronolojiye geçmek çok zor olmalı. Bu, Morozov’a bile saçma gelmişti.
İşte mesela [544]’de, 4. cilt, kısım 4, parça II, 2. bölümde N.A. Morozov Skaliger tarihlemesinin doğrulandığını düşünüp bugün V. yüzyıla ait sayılan tutulmaların birinden bahsediyor. Ancak bu açıklamadan burada Skaliger tarihlemesinin herhangi bir doğrulamasının söz konusu olmadığı bellidir. Tutulmanın tarifi gayet bulanık. Kuyruklu yıldızların tarihleme için kullanılması ise “İmparatorluk” kitabımızın kuyruklu yıldızlar listesine dair 5. bölümünde anlattığımız sebeplerden dolayı mümkün değil. N.A. Morozov M.S. IV-V. yüzyıllardan sonraki Skaliger tarihinin doğru kronolojiye dayandığına inanıp M.S. V. yüzyıldan sonraki dönemlere ait olan tutulmaları araştırırken tutarlı olmamıştı. M.S. IV. yüzyıldan önceki döneme ait olan bu kadar bulanık tarife rastlasaydı, bunları astronomi bakımından doğrulanmayan tariflerin arasına pek haklı olarak atardı.
N.A. Morozov tutulmaların bugün güya M.S. V-VI. yüzyıllarla tarihlenmiş olan diğer tariflerine karşı aynı hatayı yapmıştı. Bunlara, tutulmaların M.S. IV. yüzyıldan önceki döneme ait olduğu düşünülen tariflerden çok daha iyi niyetli bakmıştı. Burada Skaliger tarihlemelerinin doyurucu olduğunu yanlışlıkla düşünen N.A. Morozov genelde VI-XI. yüzyıllara ait sayılan tutulmaları hiç kontrol etmemiştir. Biz N.A. Morozov’dan farklı olarak eleştirel analize devam ederek, M.S. V. yüzyıldan M.S. XVII. yüzyıla kadar süren sonraki dönemi de araştırıp N.A. Morozov’un IV-V. yüzyıllarda boş yere durduğunu meydana çıkardık. Tutulma tariflerinin bugün M.S. X-XIII. yüzyıllardan önceki döneme ait olduğu kabul edilen tarihlenmelerinin astronomiye, M.S. IV. yüzyıldan önceki tutulmaların tarihlenmeleri kadar aykırı olduğu ortaya çıkmıştır. Bir uygunluğun var olması halinde ise, bu tutulmaların, XVI-XVII. yüzyıllarda yaşayan kronoloji uzmanları tarafından, o zamanlarda yaratılan Skaliger tarihinin doğrulanması için geriye, yani geçmişe doğru hesaplanmasının apaçık izleri hemen hemen her zaman bulunabilir. XVI-XVII. yüzyıllarda yaşayan kronoloji uzmanları, mesela bazı Ay tutulmalarını geçmişe doğru hesapladıktan sonra yanlış kronolojiyi sağlam bir şekilde doğrulamak için onları yaratılmakta olan “Eski Çağ” vakayinamelerine yazardı. Tabii ki, VI-XIII. yüzyıllarda meydana gelen Ay ve Güneş tutulmalarının seyrek olan bazı güvenilir tariflerinin XVI-XVII. yüzyıllarda yaşayan kronoloji uzmanlarına ulaşmış olabilmesi mümkündür. Ancak, bu seyrek tarifler Skaliger versiyonunun filtresinden geçirildikten sonra “doğru” tarihlere uydurulmuştu. Böylelikle, bu kitabın [544]’de başlanmış olan araştırmalara devam eden yazarı M.S. 400 ile 1600 yılları arasında kalan Orta Çağ tutulmalarını da araştırmıştır. Sonuçta, [544]’te “eski” tutulmalar için ortaya çıkarılmış olan geriye taşıma efektinin, genellikle M.S. 400-900 yıllarıyla tarihlenen tutulmalar için de geçerli olduğu ortaya çıkmıştır. Bu da ya eşit haklılığa sahip olan çok sayıda astronomik çözümün var olduğu, dolayısıyla da tarihlemenin kesin olmadığı ya da çözümlerin sayısının az, yani bir iki tane olduğu anlamına gelmektedir. Ancak o zaman hepsi 900 ile 1700 yılları arasına düşer. Hiç de N.A. Morozov’un [544]’de tahmin ettiği gibi M.S. 400 yılından itibaren değil, ancak M.S. yaklaşık 1000 yılından itibaren Skaliger’in astronomik kuralda verilen tutulma tarihlerinin N.A. Morozov’un yönteminin sonuçlarıyla uyumlaştırılması doyurucu hale gelmiş ve ancak M.S. 1300 yılından itibaren az çok güvenilir olmuştur.
Tutulmaların ve “eski” sayılan ilgili vakayinamelerin “yukarıya doğru (yani zamanımıza daha yakın olan) taşınmasını” gösteren bazı parlak örnekleri sunalım.
2.3. “Antik” Tukididis’in Tarif Ettiği Üç Tutulma
Skaliger tarihi bizi, Tukididis’in yaklaşık M.Ö. 460 yılında ya da M.Ö. 456-451 yıllarında doğup yaklaşık M.Ö. 396 yılında öldüğüne inandırmaya çalışıyor [924], s.405. Kendisi zengin Atina şehrinin aristokratı ve devlet adamıydı. Tukididis, Peloponez Savaşı sırasında stratejist olarak Atina filosunun kumandanlığını yapmıştı. Ancak pek başarılı değildi. Atina’dan 20 yıl kovulmuştu. Trakya’da yaşarken ünlü çalışmasını yazmıştır.
Tukididis savaş bitmeden önce bağışlanmıştı. Atina’ya geri döndükten kısa süre sonra ölmüştür.
TARİH, ŞAHİDİ VE KATILIMCISI OLAN TUKİDİDİS’E SAVAŞIN TARİFİ KONUSUNDA TÜMÜYLE GÜVENİYOR. Tukididis’un kendisi ise bu konuda şunu yazıyor: “Her olayın mümkün olduğu kadar kesin araştırmasını yaptıktan sonra bizzat şahit olduğum olaylar ve başkalarından duyduklarımla ilgili notlar almıştım... Bütün savaşı yaşamış oldum... onu anlayıp dikkatlice izledim.” [923], V:26.
Tukididis Peloponez Savaşı’nın tek kaynağıdır. Tarihçiler şunu yazıyorlar: “Tukididis’ten sonra Peloponez Savaşı’nın tarihiyle uğraşan yoktu. Ancak çok insan takipçiliğini yapmayı gurur okşayıcı bulup çalışmalarına Tukididis’un eserinin bittiği yerden başlardı.” [961], s.171. Kabul edilmektedir ki, ilkin, Tukididis’in çalışmasının ya hiç adı yoktu [924], s.412, ya da Yunanca “Birleşik Açılama” adı verilmişti, ama sonraki çevirilerinde “Peloponez Savaşı’nın Tarihi” adı kabul edilmişti. Tukididis’in İyonyalılar ile
Dorlar (Dor, ters okunduğunda Orda mı acaba?) arasındaki 27 yıllık savaş konusundaki tüm anlatımı, tamamlanmamış kaldığı halde apaçık ve ardışıktır.
Tukididis’in, basıldığında yaklaşık 800 sayfalık bir hacme sahip olan çalışması mükemmel bir üslupla yazılmıştı [923]. Çok sayıda yorumcu kitabın aşağıdaki özelliklerini çoktan ortaya çıkarmışlardı.
1) Tukididis çok okumuş ve yazar olarak tecrübeli olduğunu göstermişti;
2) Cümlelerin yapılışı çok zor, cümleler zor gramatik şekilleri içermektedir;
3) Tarihsel olguların anlatılmasında derli toplu, gerçekçi bir fikrin geliştiği ortada;
4) Yazar insan hayatındaki doğaüstü her şeye güvensizlikle bakıyor.
Bizi bu çalışmanın, yazı malzemelerinin pahalı ve seyrek olduğu, Mezopotamya’da kilin kalemle çizildiği, Yunanlıların kâğıdı bilmedikleri için ağaç kabuğunun parçalarında ya da ince değneklerle mumla kaplanmış olan tahta parçalarında yazdıkları M.Ö. V. yüzyılda yazıldığına inandırmaya çalışıyorlar.
Tukididis’in “Tarihi’nin” en eski nüshasının, Floransa’da tutulan, güya X. yüzyıla ait olan Codex Laurentinianus parşömen kâğıdı olduğu düşünülmektedir. Bütün diğer eski elyazmaları güya XI-XII. yüzyıllara aittir [924], s.403. Mısır’da, XIX. yüzyılda Tukididis’in ikinci kitabından alınan bazı başka papirüs parçaları bulunmuştu. Ayrıca, ancak 1908 yılında yayımlanmış olan bir papirüs yorumu bugüne ulaşmıştır. Ancak bu parçalar çok bozulmuş şekilde bulunmuştu [544], cilt 4., s.495. Hemen kaydedelim ki, adlarını saydığımız bütün “Eski Çağ” elyazması tarihlemeleri sadece paleografi hipotezlerine dayandığı için fazla güven vermez. Kronolojinin bir şekilde değiştirilmesi otomatik olarak bütün bu “paleografi tarihlerini” değiştirir.
Tukididis’in “Tarihi’nde” bir türlü takvim tarihlerinin sözü geçmiyor, gezegen horoskoplarından bahsedilmiyor. Ancak iki Güneş tutulması ve bir Ay tutulması dâhil olmak üzere üç tutulmanın tarifi var. Bu tertibe üçleme diyelim. Ayrıca, birinci I:23 kitabında Güneş tutulmalarından bahsedilmektedir ancak bunlar gayet genel ve belirsizdir ve astronomik tarihlemeye hizmet etmemektedir. Üçlemenin tarifleri ise kesin çözüme ulaşmak için oldukça uygun. Şimdi buna geçelim.
“Tarih”in ikinci kitabında, Güneş tutulması oldukça ayrıntılı bir şekilde tarif edilmiştir. Tukididis’in, XIX. yüzyılda F.G. Mischenko’nun yaptığı ünlü profesyonel çevirisini kullanalım [923]. Tukididis şunu yazıyor: “Aynı yaz boyunca İyonyalılar Aegina şehrinden Aeginalıları eşleri ve çocuklarıyla kovmuşlardı (savaşın ilk yılı söz konusu - A.F.)... Aynı yaz boyunca yeniay çıktığında (bunun sadece böyle günlerde olması mümkün) ÖĞLEDEN SONRA GÜNEŞ KAPANIP, YARIMAY BİÇİMİNİ ALARAK YİNE TAMAMLANMIŞTI VE BİRKAÇ YILDIZ ORTAYA ÇIKMIŞTI.” [923], II:27-28. Yunanca metni res.2.3’d e gösterilmiştir.
e gösterilmiştir.
Dikkat edelim ki, yazarın, mutlaka yeniay olması gerektiğini söyleyerek, tutulma mekanizmasını çok iyi anladığı görülüyor. Herhalde bu, insanların Tukididis’in yaşadığı dönemde tutulma gözlemi konusunda artık büyük bir tecrübesinin olduğuna işaret ediyor.
Üçlemenin yine Güneş tutulması olan ikinci tutulması Peloponez Savaşı’nın sekizinci yılında, üstelik yazın başlangıcında ortaya çıkıyor. Tukididis dördüncü kitabında şunu yazıyor: “Kış bitmiş ve tarihini Tukididis’in yazdığı savaşın yedinci yılı da bitmiştir. SONRAKİ YAZIN BAŞINDA YENİAY ÇIKTIĞI ZAMAN PARÇALI GÜNEŞ TUTULMASI ORTAYA ÇIKMIŞTI.” [923], IV:51-52. Yunanca metni res.2.4’de gösterilmiştir.
gösterilmiştir.
Tukididis yaz seferinin başladığı yaz ayından bahsediyor. Muhtemelen sözü geçen yaz ayı genellikle savaş seferlerinin başladığı bir ay olan Mars’ın ayı Mart’tır. Bu düşüncenin, problemin kesin çözümü bulunduktan sonra kontrol edilmesi ilginç olur.
Üçüncü Ay tutulması yedinci kitapta tarif edilmiştir. “Kış bitmek üzereydi, tarihini Tukididis’in yazdığı savaşın on sekizinci yılı da bitiyordu. Sonraki ilkbahar gelir gelmez, Spartalılar ve müttefikleri baharın ilk günlerinde Attika’ya saldırmıştı.” [923], VII:18-19. Sonra ise ayrıntılı bir şekilde yaz olayları anlatılmaktadır. Tarif edilmiş olan savaş hareketlerinin araştırılması, sonraki 50-51. bölümlerin büyük bir ihtimalle yazın sonunu tarif ettiğini gösteriyor. Burada Tukididis şunu yazıyor: “Her şey hazırdı. Atinalıların gemileri kalkacakken AY TUTULMASI ORTAYA ÇIKTI; O ZAMAN DOLUNAY GÖRÜNDÜ.” [923], VII:50. Yunanca metnine res.2.5’de bakılabilir.
bakılabilir.
Araştırmamızın muhasebesini yapalım. Tukididis’in metninden aşağıdaki veriler alınabilir.
1) Bütün bu üç tutulma 15 ile 30 derecelik boylam ve 30 ile 42 derecelik enlem gibi tahmini coğrafi koordinatları olan bir bölgede gerçekleşmişti;
2) Birinci tutulma Güneş tutulmasıdır;
3) İkinci tutulma Güneş tutulmasıdır;
4) Üçüncü tutulma Ay tutulmasıdır;
5) Birinci ile ikinci Güneş tutulmaları arasındaki zaman aralığı 7 yıldır;
6) İkinci ile üçüncü tutulmalar arasındaki aralık 11 yıldır;
7) Birinci tutulma yaz döneminde gerçekleşmişti;
8) Birinci Güneş tutulması yıldızlar göründüğü için tam olan bir tutulmadır, yani evre değeri 12 puandır. Hatırlatalım ki, tutulma kısmi ise yıldızlar görünmez;
9) Birinci Güneş tutulması mahalli saate göre öğleden sonra meydana gelmişti;
10) İkinci Güneş tutulması yazın başında meydana gelmişti;
11) Ay tutulması yazın sonunda meydana gelmişti;
12) İkinci Güneş tutulması tahmini olarak Mart’ta meydana gelmişti. Mamafih, bu düşünceyi bu listeye dâhil etmeyebiliriz.
Amacımız 1-11 No’lu bütün şartlara uygun olan astronomik çözümü bulmaktır.
Üç tutulmanın “antik” çalışmadaki bu kadar net tarifi tarihçilerin ve kronoloji uzmanlarının dikkatini doğal olarak çekmiştir ve bunları tarihlemeye çalışmışlardır. Görünen o ki, kronoloji uzmanları Skaliger tarihinde aşılmamış olan ciddi zorluklarla hemen karşılaşmışlardı. Tukididis’in üçlemesi ile ilgili tarihleme sorununu Ginzel’in ünlü astronomik çalışmasına uyarak daha ayrıntılı bir şekilde anlatalım [1154], s.176-177.
XVI. yüzyılda kronoloji uzmanı Dionisius Petavius birinci tutulmanın tarihini bulmuştur. Ona göre tutulma 3 Ağustos M.Ö. 431 tarihinde gerçekleşmiştir. Johannes Kepler daha sonra bu tarihte tutulmanın gerçekten ortaya çıktığını doğrulamıştır. O zamandan beri Peloponez Savaşı’nın Skaliger tarihi M.Ö. 431 yılı olarak saptanmıştır.
D. Petavius ikinci tutulmanın tarihini 21 Mart M.Ö. 424 olarak tespit etmişti. J. Kepler bu tarihte de tutulmanın gerçekten ortaya çıktığını doğrulamıştı.
D. Petavius üçüncü tutulmanın tarihini 27 Ağustos M.Ö. 413 olarak tespit etmişti.
Böylelikle astronomi Tukididis tarafından tarif edilen olayları M.Ö. V. yüzyıl ile tarihlemiş gibi görünüyor. Ancak Petavius tarafından önerilen “astronomik çözüm” tekrar araştırılırken ciddi zorluklar ortaya çıkmıştır. Bu zorluklar XVIII-XX. yüzyıllar boyunca hem astronomik literatürde hem de kronoloji literatüründe sürekli tartışılmıştır. Bu şiddetli tartışmalar birkaç kere ortaya çıkmış ve sonra durulmuştu. Mamafih, çağdaş tarihçiler “sorun yok ve hiçbir zaman yokmuş” gibi yaparak bu uzun ve zor tartışmadan bahsetmeden geçmeyi tercih ediyorlar.
Kronoloji uzmanları birinci tutulmayı araştırırken tarihleme ile ilgili asıl problemlerle karşılaştılar. Mesele şudur ki, Petavius’un teklif ettiği 3 Ağustos M.Ö. 431 tarihli tutulmanın HALKA BİÇİMİNDE OLAN tutulma olduğu ortaya çıktı. Dolayısıyla BU TUTULMA DÜNYANIN HİÇBİR YERİNDEN TAM ŞEKİLDE GEÇMEMİŞTİ. Bu, Peloponez Savaşı’nın Skaliger “astronomik tarihi” Skaliger kronoloji cetvellerine alındığında ortaya çıkmıştı. Ginzel’in kanununda da bu tutulmanın tam halka biçiminde olan bir tutulma olduğu kaydedilmişti [1154], s.176. Bu tutulmanın halka biçiminde olduğu olgusu tutulma hesaplanmasına ait bugün var olan bilgisayar programlarına göre kontrol edilmektedir. Biz onu, 1995 yılında Moskovalı astronom A. Volynkin tarafından icat edilmiş olan yaklaşık hesaplamalara uygun ve basit Turbo-Sky bilgisayar programını kullanarak kontrol ettik. Evet,
3 Ağustos M.Ö. 431 tarihli tutulmanın HALKA BİÇİMİNDE OLAN tutulma olduğu gerçektir.
Ancak Tukididis tutulma sırasında yıldızların göründüğünü kesin olarak söylüyor ki. Söylediğimiz gibi, kısmi tutulma sırasında yıldızlar görünmez. Üstelik “Petavius’un” M.Ö.
431 yılında Atina’da ortaya çıkan tutulmasının evresinin hiç de büyük olmadığı ortaya çıkmıştır. J. Kepler de “Optik”inde bu tutulmanın evresinin 12 puan olduğunu, yani tutulmanın tam olduğunu söyleyip yanılmıştır. J. Kepler’in bu düşüncelerini onun zamanında tutulma hesaplama yöntemlerinin yetkin olmamasıyla açıklayabiliriz. Tutulma evresinin hesaplanması oldukça nazik bir iştir. Mamafih, kronoloji ile çok uğraşan ve tutulma sadece tam olurken yıldızların göründüğünü iyice anlayan astronom J. Kepler’in M.Ö. 431 yılına ait çözümü biraz çarpıtıp, işine geldiği gibi yapmaya karar vererek kısmi tutulmayı tam tutulmaya dönüştürmüş olması da mümkündür. Bunu da Tukididis’in tarifine uygun olmak ve Skaliger kronolojisinin bünyesine uyumsuzluk getirmemek üzere yapmıştır. J. Kepler, Skaliger ile yazışarak onunla devamlı olarak temasta bulunmuştu.
Yukarıda söylediğimiz hal ve şartlardan dolayı, astronomi ve kronoloji uzmanları M.Ö. 431 tarihli tutulmanın evresini yeniden hesaplamaya başlamışlardı. Aynı zamanda Atina şehri ve çevresinden gözlemlenen tutulmanın evresini, mümkün olduğu kadar, 12 puana yaklaştırmak için Ay hareketi denklemine farklı düzeltmeler yapılıyordu. “Tukididis’in üçleme sorununu” araştıran en ünlü bilim adamlarından bazılarının isimlerini belirtelim. Bunlar Petavius, Zech, Heis, Struyck, Kepler, Riccioli, Hofman, Ginzel, Johnson, Lynn, Stockwell, Seyffarth’tır.
Petavius’a göre, Atina’daki tutulmanın evresi 10''25 idi [1337]. Struyck’a göre 11'', Zech’e göre -10''38, Hofman’a göre - 10''72, Heis’e göre yalnız -7''9 idi (!) [1154], s.176-177. “Tukididis’in yıldızları” sorunu ile büyük bir özenle uğraşan Ginzel 10’’ evresini elde etmişti [1154], s.176-177. Tutulmanın halka biçiminde bir tutulma olmakla kalmayıp Atina’da oldukça kısa evreye sahip olan kısmi bir tutulma olarak gözlendiği apaçık ortaya çıkmıştı. 3
Ağustos M.Ö. 431 tarihli tutulma sırasında Ay gölgesinin yeryüzünden geçme hattı рис.2.6 ’da kesikli çizgi ile işaretlenmiştir. Bu, Güneş tutulmasının halka biçiminde bir tutulma olduğu anlamına gelmektedir. Tam gölge hiçbir yerde tespit edilmemişti.
’da kesikli çizgi ile işaretlenmiştir. Bu, Güneş tutulmasının halka biçiminde bir tutulma olduğu anlamına gelmektedir. Tam gölge hiçbir yerde tespit edilmemişti.
Atina’da ortaya çıkan M.Ö. 431 tarihli tutulmanın evresinin yaklaşık 10 puan oluşturması Güneş kursunun 1/6’sının açık olduğu anlamına gelmektedir. Bu, hemen hemen aydınlık bir gündü! Elbette ne bir gezegen ne de yıldızlar görünüyordu. Üstelik рис.2.6 ’dan çıktığı gibi, bu tutulma Kırım’dan mahalli saate göre sadece on yediyi yirmi iki dakika geçe,
’dan çıktığı gibi, bu tutulma Kırım’dan mahalli saate göre sadece on yediyi yirmi iki dakika geçe,
Heis’e göre ise ancak on altıya altı dakika kala geçmişti. Dolayısıyla, bu tutulmanın, Tukididis’in söylediği gibi öğleden sonra ortaya çıkması zorlukla kabul edilebilir. Bu, daha ziyade bir akşam tutulmasıdır.
Çağdaş, yaklaşık hesaplamalara uygun Turbo-Sky programını kullanıp Atina ve çevresini gözlem noktası olarak göz önünde bulundurarak evrenin azami olduğu anda Ay ve Güneş’in konumunu hesapladık. Sonucumuz рис.2.7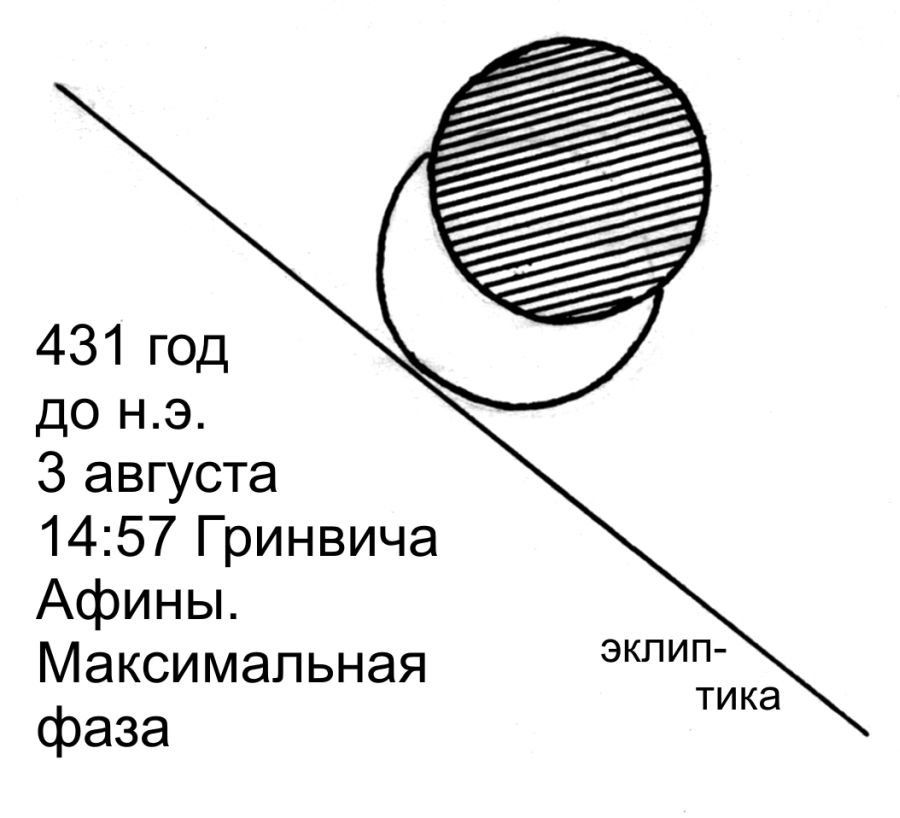 ’de gösterilmiştir. Güneş kursunun daha büyük parçasının açık olduğu ortada. Herhangi bir gezegenin ya da yıldızların göründüğünden söz edilemez.
’de gösterilmiştir. Güneş kursunun daha büyük parçasının açık olduğu ortada. Herhangi bir gezegenin ya da yıldızların göründüğünden söz edilemez.
Böylelikle Petavius’un önerdiği 3 Ağustos M.Ö. 431 tarihli tutulma 8 ve 9 numaralı şartlara uymadığı için Tukididis’in tarif ettiği tutulma olamaz.
Bu durumun bulunmasının Skaliger kronoloji uzmanları ve Skaliger tarihçileri için pek tatsız olduğu belli. Astronom Ginzel bu konuda şunu bile yazmıştır: “Yeni hesaplamalara göre Atina için 10’’ oluşturan tutulma evresinin süreksizliği BİR DERECEDE ŞOKUN VE
TUKİDİDİS’İN DOĞRULADIĞI GİBİ, “YILDIZLARIN GÖRÜNDÜĞÜ” ŞÜPHELERİNİN ORTAYA ÇIKMASINA YOL AÇMIŞTI.” [1154], s.176.
Yıldızlar M.Ö. 431 tarihli tutulma sırasında net görünmediği için, Heis ve Lynn bunun durumu kurtarmaya yardım edeceği umuduyla, parlak gezegenlerin konumlarını hesaplamaya karar vermişlerdi. Ancak Mars’ın ufuğun üstünden sadece üç derecelik yükseklikte olduğu ortaya çıkmıştı. Venüs yukarıdaydı, ufuktan 30 derecelik yükseklikte. Grinzel, Venüs ve Mars konusunda bu iki gezegenin “görünür olmasının mümkün olduğunu” ihtiyatlı bir şekilde söylüyor [1154], s.176. Ancak gök hemen hemen açık olduğu takdirde bunun ihtimali düşük. Dolayısıyla bütün ümitler Jüpiter ve Satürn’e bağlanmıştı. Ancak, Jüpiter tutulma sırasında zaten UFUĞUN ALTINDA olduğu için hiç görünmüyordu. Satürn ise ufuğun üstünde olduğu halde Terazi’nin içinde, güneydeydi ve oldukça uzaktı. Ginzel’in yazdığı gibi, “onun göründüğü fikri son derece şüpheliydi [sehr zweifelhaft]” [1154], s.176.
Turbo-Sky programını kullanarak 3 Ağustos 431 tarihli tutulmanın ortaya çıktığı anda
gezegenlerin konumunu hesapladık, bkz. рис.2.8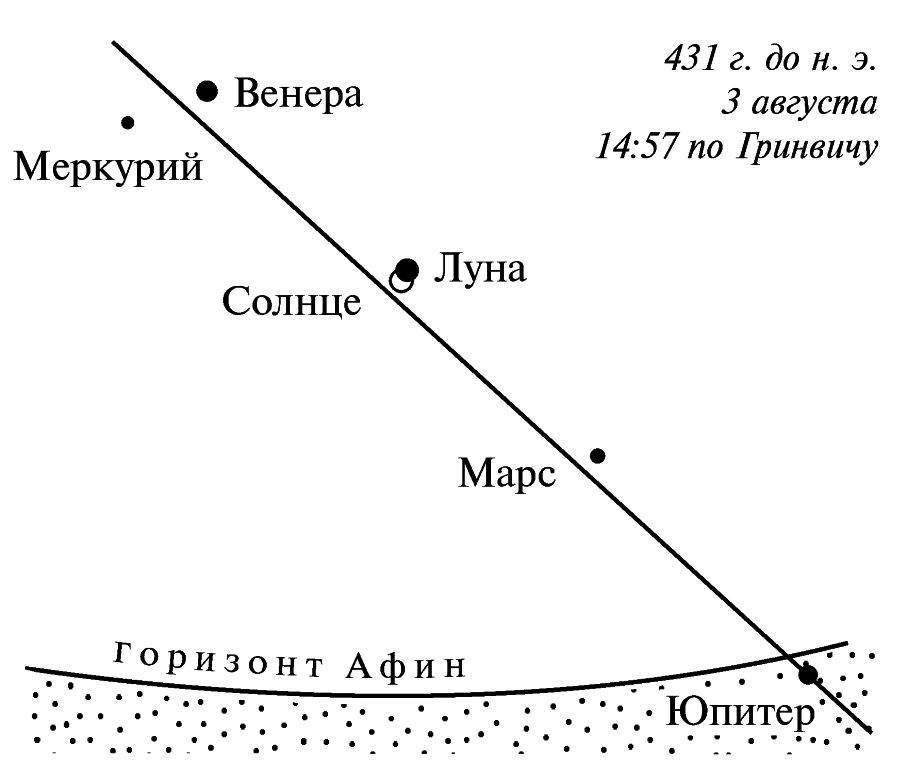 . Burada tutulma evresinin azami olduğu anda Greenwich’e göre saat 15’e 3 dakika kala Atina’dan görülen göğün görünüşü gösterilmiştir. Venüs, Mars ve çok daha donuk olan Merkür Güneş’e yakın olduğu için sadece kısmen kapanmış olan Güneş’in ışınlarında kayboluyordu. Demek ki, fiilen açık bir günde görünmeleri ihtimali gerçekten çok az.
. Burada tutulma evresinin azami olduğu anda Greenwich’e göre saat 15’e 3 dakika kala Atina’dan görülen göğün görünüşü gösterilmiştir. Venüs, Mars ve çok daha donuk olan Merkür Güneş’e yakın olduğu için sadece kısmen kapanmış olan Güneş’in ışınlarında kayboluyordu. Demek ki, fiilen açık bir günde görünmeleri ihtimali gerçekten çok az.
Skaliger kronolojisi için ortaya çıkan bu zor durumda, Johnson 30 Mart M.Ö. 433 tarihinde meydana gelen bir başka tutulmayı teklif etmiştir. Ancak, bu hiçbir üçlemenin parçası değildir. En yakın üçlemeler şunlar: M.Ö. 447, 441 ve 430 yılları ve M.Ö. 412, 405,
394 yılları. Ama bunlar başka sebeplerden dolayı uygun değildir. Johnson tarafından önerilmiş olan tutulma evresi sadece 7''8, yani Petavius’un işaret ettiği başarısız tutulmadan dahi daha azdır [1154], s.177.
Bunun üzerine, Stockwell evrenin hesaplamalarını, mümkünse evreyi çarpıtıp işine geldiği gibi yapmak için yeniden araştırmaya çalışmıştı. Ancak tüm hilelerine rağmen yalnız
11''06’ı elde etmeyi başarmıştı. Mamafih Ginzel, Stockwell’in hesaplarını güvensizlikle karşılamıştı.
Seyffarth çözümü bulmaya çalışarakTukididis’in belki M.Ö. 27 Ocak 430 tarihli tutulmayı kastetmiş olduğu hipotezini dile getirmişti [1154], s.177. Fakat bu tutulmanın Tukididis’in tariflerine hiç de uymaması (mesela herhangi bir üçlemeye katılmaması) bir yana, kontrolü Atina’nın yanında görülmediğini göstermişti. [1154],s.177.
Üstelik Ginzel’in bahsettiği şokun yerini bir şaşkınlık almıştı. O zaman, saf demagoji dâhil olmak üzere astronomiden uzak bambaşka düşünceler ortaya çıkmaya başlamıştı. Mesela Zech “Atina’nın açık göğüne ve Eski Çağ insanlarının güçlü görümüne” atıfta bulunarak “sorunu ortadan kaldırmaya” çalışmıştı [1154], s.177’den alıntı. Çağdaş insan
elbette yıldızları hiç görmeyecekti, ama Eski Çağ insanları bambaşkaymış. Bizimkinden çok daha güçlü görüme sahipmiş. Hem de daha hızlı koşuyorlarmış.
Hofman daha da ileri giderek Tukididis’in yıldızlarının sadece retorik süslemeler olduğunu iddia etmiştir [1154], s.177. “Bütün başka konularda ona kayıtsız şartsız güveniyoruz ama bu konuda güvenmeyeceğiz”, diyor. Üstelik Hofman fikrini dilbilimsel düşüncelerle temellendirmeye çalışmıştı. Tukididis yıldızların Güneş artık hilal şeklini aldığında ortaya çıktığını bildiriyormuş. Ricamız üzerine filolog E.V. Alekseeva (Moskova Devlet Üniversitesi, Filoloji bölümü, 1976 yılı) Yunanca metnin filolojik analizini yaptı. Bkz. Ek 1. Meğer dilbilim açısından Tukididis aşağıdaki dört olayı haber vermiş. 1) Güneş kapanmış. 2) Güneş hilal şeklini almış. 3) Yıldızlar çıkmış. 4) Güneş yine eski şeklini almış.
Böylelikle tüm tutulma süreci net bir şekilde tarif edilmiştir. Önce kursun karardığı ve hilale dönüştüğü, sonra ise yıldızların çıktığı (bu ancak tam tutulmanın azami evresi sırasında meydana gelir) ve ancak bundan sonra kursun eski şeklini aldığı ortaya çıkıyor. 1-4 No’lu
olayların sırası tümüyle doğal olup cümlenin gramer bünyesi ile kesinlikle tespit edilmektedir. Zaten profesyonel çevirmen F.G. Mischenko XIX. yüzyılda Tukididis’in yukarıda atıfta bulunduğumuz metnini “Eski” Yunanca’dan tam olarak bu şekilde çevirmişti [923], II:27-28. Dolayısıyla E.V. Alekseeva’nın yaptığı tekrar araştırması sadece bu klasik çevirinin doğruluğunu bir kez daha ortaya koymuş oldu. Şimdi anladığımız gibi, astronomik tarihleme sorunu ortaya çıkmasaydı doğruluğundan zaten hiç kimse şüpheye düşmezdi.
Bu yüzden, Hofman’ın çağdaş astronom Robert Newton’un da paylaştığı fikri çeviriye değil, Skaliger kronolojisini kurtarmak dileğine dayanmaktadır. Dilbilimini astronominin yerine koymak teşebbüsünün soruna çözüm olamadığını görüyoruz.
Bütün bunlara rağmen Petavius’un yanlış tarihi değiştirilmeden kalmıştır. Bugün, bu konuda Petavius’un fikrinden başka herhangi bir sebep olmadığı için tarih konusundaki her türlü ders kitabında Peloponez Savaşı’nın M.Ö. 431 yılında başladığı bulunabilir. Böylece Tukididis’in net ve apaçık açıklamasına bariz aykırılığına rağmen Petavius’un kronolojisi
meşrulaştırılmıştır.
Metnin ayrıntılı ve sağlam şekli ve durumu metnin kendisini değiştirerek düzeltmeye yönelik her teşebbüsü ciddiyetsizlikle karşı karşıya bırakır. Hofman’ın çözümünün yanı sıra, mesela birbirine yakın olan (komşu) tutulmalar arasındaki (Tukididis’e göre 7 ve 11 yıl süren) aralıkların sürekliliğinin değiştirilmesi teklif edilmişti. Ancak bu teklifin yazarları tekliflerini açıklamaktan vazgeçmişlerdi.
Tukididis’in birinci tutulmayı tarif ederken tam tutulmayı kastettiğinden şüphe etmek zordur. Kısmi olan ikinci tutulma konusunda “yeniaydan biraz önce Güneş’in kısmi tutulması ortaya çıktı” diye net bir şekilde bildirmişti ki [923], IV:52. Yani “kısmi” sözünü kullanmıştı. Yazar galiba kısmi ile tam tutulmalar arasındaki farkı zaten çok iyi anlamıştır. Dolayısıyla o, birinci olay için sadece tam tutulma sırasında mümkün olan yıldızların ortaya çıktığını mahsus vurgulamıştı.
Araştırmamızın muhasebesini yapalım. Astronomlar M.Ö. 600-200 yılları aralığı için daha uygun bir çözüm bulamadılar. Ancak onlardan hiçbirinde arama aralığını Orta Çağ’a kadar genişletme düşüncesi uyanmamıştı. Bunun sebebi belli. Bunların hepsi Skaliger kronolojisini öğrenerek yetiştirilmiş ve ona genel olarak güvenmişlerdi. Sonuçta Petavius’un bu yanlış üçlemesi bu “çözümün” Tukididis’in metnine aykırı olduğu bilimsel literatürde çok kez tartışıldığı halde ayakta kalmıştı. Nesnel tarihleme yöntemlerinin M.Ö. 900 ile M.S. 1700 yılları arasındaki tüm aralıkta uygulanması KESİN ASTRONOMİK ÇÖZÜMÜN HER ŞEYE RAĞMEN VAR OLDUĞUNU gösteriyor. Bu çözüm [544]’de N.A. Morozov tarafından bulunmuştu, 4.cilt, s.509. Sonra ise, A.T. Fomenko “Eski Çağ” ve Orta Çağ tutulmalarını tekrar araştırdığında problemin bütün şartlarına hemen hemen tümüyle uygun olan yeni bir astronomik çözüm bulundu (ayrıntılar için aşağıya bakınız). Başka çözüm yoktur.
Kesin olan çözüm (N.A. Morozov) tam Güneş tutulması için M.Ö. 2 Ağustos 1133 tarihi, tam Güneş tutulması için M.Ö. 20 Mart 1140 tarihi, Ay tutulması için M.Ö. 28 Ağustos
1151 tarihidir.
Daha az kesin olan çözüm (A.T. Fomenko) tam Güneş tutulması için M.Ö. 22 Ağustos
1039 tarihi, kısmi Güneş tutulması için M.Ö. 9 Nisan 1046 tarihi, Ay tutulması için M.Ö. 15
Eylül 1151 tarihidir.
Morozov’un çözümü kesin olan tek çözümdür. 12 No’lu şarta bile uyar. Üstelik üçlemenin birinci tutulması Tukididis’in tarif ettiği gibi gerçekten tam bir tutulmadır. Böylelikle Skaliger kronolojisinin astronomlara bağladığı zincirlerden vazgeçerek, Tukididis’in kitabındaki astronomik tariflerinden dolayı gökbilimcileri çoktandır ilgilendirmekte olan soruya cevap verilmesi başarılmıştı.
Artık bildiğimiz tüm olguları göz önünde bulundurarak, bulunmuş iki çözümden tarihi gerçekliğe en uygun olanının Morozov üçlemesinin olduğu yargısına varabiliriz. Bu, XII. yüzyılın ortasına ait olan, yani M.S. 2 Ağustos 1133 tarihi, M.S. 20 Mart 1140 tarihi, M.S. 28
Ağustos 1151 tarihlerinde ortaya çıkmış olan tutulmalardan ibaret daha geç bir üçlemedir. XI. yüzyılın çözümü büyük bir ihtimalle çok erkendir. Res.2.9’da , Morozov tarafından bulunmuş M.S. 133, 1140 ve 1151 yıllarının çözümü gösterilmiştir. Burada hem yeryüzündeki Ay gölgesinin M.S. 1133 ve 1140 yıllarında ortaya çıkmış olan tam Güneş tutulmaları için yörüngesi hem de M.S. 1151 yılında ortaya çıkmış olan Ay tutulmasının başucu görüş noktası tasvir edilmiştir.
, Morozov tarafından bulunmuş M.S. 133, 1140 ve 1151 yıllarının çözümü gösterilmiştir. Burada hem yeryüzündeki Ay gölgesinin M.S. 1133 ve 1140 yıllarında ortaya çıkmış olan tam Güneş tutulmaları için yörüngesi hem de M.S. 1151 yılında ortaya çıkmış olan Ay tutulmasının başucu görüş noktası tasvir edilmiştir.
Bu söz konusu çözümleri Turbo-Sky bilgisayar programı yardımıyla kontrol ettik. 22
Ağustos 1039 tarihli ve M.S. 2 Ağustos 1133 tarihli tam tutulmaları niteleyen kesin verileri sunalım. Bunlar T. Oppolzer’in Tutulmalar Kanununda tam tutulmalar olarak kaydedilmiştir [544], 5.cilt, s.77-141. Turbo-Sky programı onları da tam tutulmalar olarak tespit ediyor. 2
Ağustos 1133 tarihli tutulma için yeryüzündeki Ay gölgesinin yörüngesinin başlangıcı, ortası ve sonuna ait olan coğrafi koordinatları sunalım. Birinci satırda boylamı, ikinci satırda enlemi yazılmıştır.
| -89 +8 +72 +52 +53 +9 |
Güneşi tümüyle kapatan Ay’ın gölgesi Greenwich’e göre saat 11.15 ile saat 11.17
(Turbo-Sky programı) arasında yörüngenin orta noktasındaymış (yani öğle güneşi sırasında).
XI. yüzyılın ikinci üçlemesine ait olan 22 Ağustos 1039 tarihli tutulma için Güneşi tümüyle kapatan Ay’ın gölgesi Greenwich’e göre yaklaşık saat 11’i 15 dakika geçe (Turbo- Sky programı) yörüngenin orta noktasındaymış (yani öğle güneşi sırasında). Bu noktanın koordinatları aşağıdadır: 7 derece doğu boylamı ve 45 derece kuzey enlemi (Turbo-Sky programı). Ancak, sonra ise diğer bir astronomik StarCalc programının (ikinci çözüme ait olan) 22 Ağustos 1039 tarihli tutulmayı tutulma eksenindeki evresi hemen hemen tam olduysa da, halka biçimdeki tutulma olarak gösterdiği ortaya çıkmıştı. Böylelikle kullanmış olduğumuz üç hesaplama algoritmasından ikisi bu Güneş tutulmasını tam tutulma olarak gösterirken biri de onu halka biçimindeki tutulma olarak gösteriyor. Hangi hesaplama programının daha doğru olduğuna yönelik analizin derinine inmemeyi tercih edip, ikinci çözümün nitelemeleri açısından aranmakta olan çözüme oldukça yakın olduğu halde Morozov tarafından bulunmuş olan çözümden aşağı kaldığını düşünüyoruz. Başka bir deyişle, tüm şartlara uygun olan tek ideal çözümün onun çözümü olduğu ortaya çıkmıştır. Dolayısıyla Tukididis’in tasviri XII. yüzyıla aittir.
N.A. Morozov XII. yüzyıldaki üçlemenin 2 Ağustos 1133 tarihli tutulması konusunda şunu yazmıştı: “Güneş, Hudson Körfezi’nin güney sahilinde tam tutulmadaki doğan güneş şeklinde ortaya çıkıp öğleden önceki güneş şeklinde de İngiltere’de ortaya çıkmıştı. Hollanda’da öğle güneşi şeklinde, Almanya’da, Avusturya’da, İstanbul Boğazı’nın yanında, Mezopotamya’da, Arap Körfezi’nde ise öğleden sonraki güneş şeklinde ve Hint
Okyanusu’nda tam tutulmadaki batan güneş şeklinde meydana gelmişti.” [544], 4. cilt, s.508.
Tam tutulma derin olmuş, karanlık basmış ve tabii ki, gökte yıldızlar ortaya çıkmıştı.
N.A. Morozov’un bulduğu XII. yüzyıldaki üçleme aşağıda sunulmuştur.
1) 2 Ağustos 1133 tarihli birinci tam Güneş tutulması aşağıda gösterildiği gibi geçiyordu:
| -89 +8 +72 +52 +53 +9 |
Ay gölgesinin yörüngesinin yeryüzündeki orta noktasından Greenwich’e göre yaklaşık saat 11.15 ile saat 11.17 arasında geçilmişti, bkz. рис.2.9 . Ayrıca bkz. [544], 5.cilt, s.122.
. Ayrıca bkz. [544], 5.cilt, s.122.
2) 20 Mart 1140 tarihli ikinci tam Güneş tutulması aşağıda gösterildiği gibi geçiyordu:
| -96 -30 +48 +20 +42 +55 |
Ay gölgesinin yörüngesinin yeryüzündeki orta noktasından Greenwich’e göre yaklaşık saat 14’e 20 dakika kala geçilmişti (T. Oppolzer Kanonu) [544], 5. cilt, s.123. Bkz. рис.2.9 .
.
3) M.S. 28 Ağustos 1151 tarihli kısmi Ay tutulmasının azami evresi Greenwich’e göre saat 23’ü 25 dakika geçe 4 puandı. Ay başucu görüşü sırasında koordinatları 8 derece doğu boylamı ve 7 derece güney enlemi olan noktanın üzerindeydi [544], 5. cilt, s.51.
XII. YÜZYILA AİT OLAN BU ÜÇLEME HER BAKIMDAN UYGUNDUR. Bu arada ikinci tutulma, Tukididis’in metnine göre beklenmesi gerektiği gibi gerçekten Mart’ta ortaya çıkmıştır, yukarıya bakınız.
A.T. Fomenko tarafından bulunmuş olan (daha az derecede güvenilir) XI. yüzyıldaki
üçleme aşağıda sunulmuştur:
1) 22 Ağustos 1039 tarihli birinci tam (ya da evresi hemen hemen tam olan halka
biçimindeki) Güneş tutulması aşağıda gösterildiği gibi geçiyordu:
| -82 +7 +64 +55 +45 +2 |
Ay gölgesinin yörüngesinin yeryüzündeki orta noktasından Greenwich’e göre yaklaşık saat 11’i 15 dakika geçe geçilmişti. Ayrıca bkz. [544], 5.cilt, s.118.
2) 9 Nisan 1039 tarihli, ikinci (kısmi) Güneş tutulması aşağıda gösterildiği gibi geçiyordu:
| +22 +87 +170 +19 +47 +50 |
Ay gölgesinin yörüngesinin yeryüzündeki orta noktasından Greenwich’e göre yaklaşık saat 6’ya 14 dakika kala geçilmişti (T. Oppolzer Kanonu) [544], 5.cilt, s.123.
3) M.S. 15 Eylül 1057 tarihli kısmi Ay tutulmasının azami evresi Greenwich’e göre saat 18’i 9 dakika geçe 5 puandı. Ay başucu görüşü sırasında koordinatları 86 derece doğu boylamı ve 1 derece güney enlemi olan noktanın üzerindeydi [544], 5.cilt, s.49.
Tukididis’in tutulma üçlemesi “Tukididis’in Peloponez Savaşı’nın Tarihi”nin XI. yüzyıldan önce olmayan bir dönemde yazıldığı konusunda çok inandırıcı bir kanıttır. Hatta büyük bir ihtimalle XII. yüzyıldan önce olmayan bir dönemde. Üçlemenin yazarı tarafından uydurulmuş olma ihtimali düşüktür. Yoksa o zaman, gerçek astronomi çözümü büyük bir ihtimalle hiç bulunamazdı. Bununla beraber, kesiksiz ve ayrıntılı anlatıma pek iyi uyduğu için, bu tutulmaları “antik” metne eklemeler olarak kabul etmek de zordur.
N.A. Morozov muhtemelen haklı olarak şunu yazmıştır: “Tukididis’in kitabı Eski Çağ’a, Orta Çağ’a ait olmayıp en azından on üçüncü yüzyıla, Rönesans’a aittir.” [544], 4.cilt, s.531.
2.4. “Antik” Titus Livius’un Tarif Ettiği Tutulmalar
Başka örnekleri verelim. Detayları geçip, T. Livius’un “Tarihi’ndeki” (XXXVII,4,4), bugün kronoloji uzmanları tarafından M.Ö. 190 yılı ya da 188 yılına götürülen tutulmanın Titus Livius’un tarifine uymadığını bildirelim. Tukididis’in tutulmaları ile olan durum tekrarlanmaktadır. Nesnel astronomik tarihleme sırasında, M.S. 900 ile M.S. 1600 yılları aralığında tek kesin çözümün olduğu ortaya çıkıyor. Bu çözüm M.S. 967 yılıdır [544].
Titus Livius’un “Tarih”te (LIV, 36,1) tarif ettiği Ay tutulması konusunda benzer bir durum ile karşı karşıyayız. Skaliger kronoloji uzmanları Titus Livius’un M.Ö. 168 tarihli tutulmayı tarif ettiğinin kabul edilmesini teklif ediyorlar. Ancak araştırmanın gösterdiği gibi, bu tutulmanın nitelemeleri Titus Livius’un tariflerine uymuyor. Livius tarafından tarif edilen tutulma gerçekte 4 ila 5 Eylül gecesi M.S. 415, 4 ila 5 Eylül gecesi M.S. 955, 4 ila 5 Eylül gecesi M.S. 1020 tarihlerinden birinde ortaya çıkmıştır.
Örneklerin listesi, ayrıntılı bir şekilde tarif edilmiş olan bütün “antik” tutulmaları içermektedir. Eski Çağ tutulmalarının tarihlerinin bu yukarıya kaldırılmasını gösteren tam tablosunu aşağıda sunacağız.