Part 2.
China. The new chronology and conception of Chinese history. Our hypothesis.
Chapter 5.
Chinese comets.
5. Comet Halley.
5.1. Introduction.
Comet Halley is the most famous comet of all.
Comet Halley is also the most spectacular comet of all.
Comet Halley is one of the primary foundations of Chinese chronology and the modern theory about the great antiquity of the Chinese civilisation.

Fig. 5.6. Comet depicted on an ancient carpet from Baille. Historians identify it as Comet Halley and date the observation to the alleged year 1066. The carpet was presumably made around 1073-1083. It is kept in the city library of Baille and made of wool on linen. The picture is reproduced in [930] as a fragment of “the longest and the most famous mediaeval carpet that can also serve as a historical chronicle” ([930], page 161). Taken from 930, page 161. See also the drawn copy in [544], Volume 6, page 144. The correct dating of Baille carpet is 1495 A.D. See our book “Baptism of Russia”, Ch.1.
It is believed that the Chinese observed all of this comet’s forthcomings between the I century B. C. and the present at the very least. It is believed that the modern theory of Comet Halley’s motion is confirmed by the ancient Chinese chronicles; this theory, in turn, confirms the Scaligerian chronology of China. In fig. 5.6 we reproduce an ancient representation of a comet from the ancient carpet of Baille. Scaligerian history tries to convince us that the comet in question is Comet Halley as seen in the alleged year of 1066.
Even N. A. Morozov in his radical revision of many layers of the ancient history only questions the veracity of the Chinese records concerning Comet Halley before the beginning of the new era, believing them to be more or less correct afterwards.
He makes the following confused statement: “Whatever the origin of these Chinese comet records, some of them are in amazing concurrence with the theoretically calculated recurrences of Comet Halley, which makes us treat them seriously as a valid means for the verification of the ancient documents that contain comet descriptions” ([544], Volume 6, page 156).
Thus, one has no apparent reasons to be suspicious of the Chinese chronology, based on the recurrences of Comet Halley, among other things – even N. A. Morozov was convinced, although he retained a number of serious suspicions: “Comet Halley does not substantiate the reports of She-Ke and the “Forest Horse” concerned with the first centuries A. D. What right have we to assume that these books can prove any chronological scale extending further back into the past?” ([544], Volume 6, page 154).
However, the situation here isn’t quite as simple as it might seem originally. The analysis of N. A. Morozov proved incomplete here. He shouldn’t have considered the correspondence between some of the “ancient” Chinese records and the calculated recurrence cycle of Comet Halley “amazing” – our analysis demonstrates that the probability of said correspondence being mere coincidence is high enough; many such correspondences do in fact turn out purely coincidental, qv below. However, fortunately enough, the creators of the “ancient” Chinese chronology refused to stop here, attempting to bring the entire picture to “perfection”. They made a mistake here, having added several “ancient” Chinese records of the alleged sightings of Comet Halley in the XVIII century and thus left a criminating piece of evidence that permits proving the falsity of the entire “ancient” Chinese chronology. The forgery in question was committed in the XVIII century.
5.2. The analysis of Planet Halley’s recurrence cycles.
5.2.1. A list of the dates of Comet Halley’s alleged sightings.
Let us begin with the list of dates traditionally associated with the sightings of Comet Halley. It is usually divided into two parts, namely, the Chinese and the European records of Comet Halley’s observations. Let us cite both lists and compare them to each other.
The astronomers Cowell and Crommelin have used these dates as a basis for the astronomical and mathematical theory of Comet Halley’s motion at the very beginning of the XX century. They used this theory for their theoretical calculations of the comet recurrence cycles into the past. In the following table we cite the results of their theoretical calculations as well as the years of European and Chinese observations presumed to be related to Comet Halley. The names of months in the left column indicate the passage of the comet through the perihelion point.
| Theory (Cowell & Crommelin). Julian calendar. | Traditional dates of Chinese records (according to She-Ke) | Traditional dates indicated in European chronicles. |
April 1910 ........................................... 1910 .................................... 1910
March 1835 ........................................ 1835 .................................... 1835
March 1759 ........................................ 1759 .................................... 1759
September 1682 ........................................ 1682 .................................... 1682
October 1607 .......................................... 1607 .................................... 1607
August 1531 .......................................... 1531 .................................... 1531
June 1456 ........................................... 1456 .................................... 1456
November 1378 ........................................ 1378 .................................... ---
October 1301 .......................................... 1301 .................................... 1301
September 1222 ........................................ 1222 .................................... 1222
April 1145 ............................................ 1145 .................................... 1145
March 1066 ......................................... 1066 .................................... 1066
September 989 ......................................... 989 ..................................... ---
July 912 ............................................. 912 ..................................... 912
February 837 .......................................... 837 ..................................... 837
July 760 ............................................ 760 ..................................... -(761 ?)
November 684 ......................................... 684 ..................................... 684
March 607 ........................................... 607 ..................................... - (607 ?)
November 530 ......................................... 532 ..................................... 531
July 451 ............................................. 451 ..................................... - (450 ?)
November 373 ......................................... 373 ..................................... ---
April 295 ............................................ 296? .................................... ---
April 218 ............................................. 218 ..................................... 217
March 141 ........................................... 141 ..................................... ---
January 66 ........................................... 66 ...................................... 66
October -12 ......................................... -11 ..................................... -12
August -86 ......................................... -86 ..................................... -86
No other mentions of Comet Halley are found in either the Chinese or the European sources, apart from a few scarce exceptions. For instance, the Chinese record of 239 B. C. is occasionally considered to be a reference to Comet Halley ([544], Volume 6, page 140). See the graph of Cowell and Crommelin and the comet roster on page 73 of the abovementioned source.
The first impression one gets is that the table unambiguously leads us to the following fundamental conclusion: the mathematical theory of Comet Halley’s motion is in excellent correspondence with the observations of the Chinese. A propos, the correspondence of said theory with European sources is a great deal worse. However, let us refrain from being overly critical – after all, it is common knowledge that the Chinese astronomers were known for their meticulousness, especially in the distant past – a far cry from their European colleagues.
Let us reiterate: the theoretical graph appears to be conformed by the coincidence of all the theoretical dates with the ones taken from the Chinese chronicles, with the exception of one two-year discrepancy and two one-year discrepancies. Actually, the one-year discrepancies can be disregarded, owing to a certain ambiguity concerning the beginning of the year in the antiquity.
5.2.2. What happened to Comet Halley in 1986? The reasons why it shifted to the other hemisphere.
One must specifically mark the fact that the Chinese astronomers are believed to have observed every single apparition of Comet Halley over the course of two thousand years without missing any.
China is located in the Northern Hemisphere. Apart from that, every description of the path of a comet identified as Comet Halley today refers to the constellations of the Northern Hemisphere or the Zodiac. We have checked this against the comet roster in [544], Volume 6.
The inevitable conclusion is that every single apparition of Comet Halley over the last two thousand years was theoretically observable from the Northern Hemisphere exclusively.
Everything seems understandable and natural so far. A large recurrent comet has been following the same stationary orbit, more or less stable in relation to the ecliptic, for the last two thousand years.
Let us ask the readers residing in the Northern Hemisphere whether they saw Comet Halley in 1986? The answer is in the negative. The reason is perfectly simple – it wasn’t visible from the Northern Hemisphere, and could only be observed from the Southern (being rather dim at that).
What could have possibly happened to Comet Halley? Two thousand years of observations from the Northern Hemisphere followed by a sudden migration to the Southern? Our opponents might suggest this fact to be a consequence of the mathematical law of its motion. This very mathematical law is what we shall consider in the following section.
For the time being, let us make a summary. Such a drastic change in the motion pattern of a comet that had remained stable for two thousand years strikes us as very odd indeed.
The above makes us strongly doubt the veracity of the traditional chronology of Comet Halley’s sightings. Are all of its apparitions reflected in the Chinese chronicles veraciously? Could we be faced with random coincidences or something worse still – later insertions into the text? By the way, what is the probability of an arbitrary “periodical sine curve” randomly coinciding with the accepted traditional dates as found in Chinese records? We shall provide the answer to this question below; jumping ahead, we can tell the readers that such a probability is actually rather high.
5.2.3. What has been happening to Comet Halley after 1759? The reason why its recurrence cycles have become irregular.
The sequence of dates suggested to stand for the apparitions of Comet Halley in Chinese rosters has a very odd trait. It reveals an exceptionally precise centenarian regularity in the changes of Comet Halley’s recurrence cycles, which is believed to be characterised by exceptional stability. We are referring to the law discovered by the astronomers Cowell and Crommelin, who studied the Chinese comet rosters ([544], Volume 6).

Fig. 5.7. The graph shows the fluctuations of time intervals between the observations of Comet Halley according to the Scaligerian chronology. The horizontal line corresponds to the Scaligerian Comet Halley observation dates, and the vertical – to the distances between comet observations given in years. The graph is very obviously periodical in nature; the borders of the resulting periods are indicated at the bottom.
On the horizontal axis we have the years when Comet Halley was observed according to the Chinese chronology. The dates are given with the precision margin of one tenth of a year.
On the vertical axis we see the recurrence periods of Comet Halley, or the intervals between its consecutive reappearances. For instance, the interval between its last apparition of 1986.1 and the previous one of 1910.3 equals 75.8 years etc. These numbers are indicated underneath the graph.
The graph reveals a distinct periodic regularity manifest as centenarian accelerations and decelerations in the motion of Comet Halley with a period of 77.0 years. The levelled sine curve corresponds to the modified values of recurrence intervals.
The saw-tooth curve corresponds to the consecutive recurrence periods of the comet calculated from the Chinese chronicles. We shall be calling this curve “experimental” in this regard. One must point out that the theoretical dates calculated by the astronomers for the recurrence cycles of Comet Halley are in excellent correspondence with the “Chinese experiments”. This very fact confused N. A. Morozov greatly and partially convicted him that the Chinese dates of Comet Halley’s sightings over the last fifteen hundred years of the new era were veracious.
Now let us analyse the saw-tooth “Chinese experimental” curve. It turns out that the scatter range of “experimental” dots around the sine curve is also far from random. This saw-tooth graph, presumably experimental, is also strictly periodic de facto. Three of its periods are indicated in fig. 5.7:
1) Between the alleged years 551 B. C. and 218 A. D. (apparent extrapolation, since the Chinese are assumed to have lacked the information concerning Comet Halley for some part of this epoch),
2) Between the alleged years 218 A. D. and 989 A. D.,
3) Between the alleged years 989 A. D. and 1759 A. D.
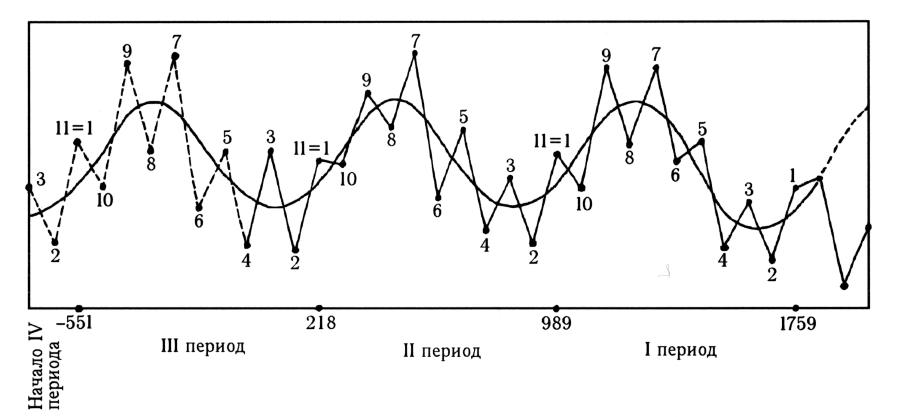
Fig. 5.8. Previous graph of fluctuating time intervals between the observations of Comet Halley. Here we have assigned the same number to every corresponding point within a given period.

Fig. 5.9. Superimposition of three fictional periods
in the behaviour of Comet Halley.
This goes to say that Comet Halley behaved
in the exact same manner thrice.
IIn fig. 5.8 we have assigned a number from 1 to 10 to the “experimental” dots comprised by each period. It is perfectly obvious that the segment of the saw-tooth curve numbered 1, 2, . . ., 10 repeats itself three times, almost without variations.
This effect is particularly demonstrable in fig. 5.9, where said three segments of the saw-tooth curve are superimposed over each other. Despite the minor discrepancies between the three curves, we can clearly see that they are virtually identical.
Thus, the “experimental” curve of Comet Halley’s recurrence periods is strictly periodic, the period being roughly equal to 77 years. Therefore, it would be normal to expect this law, which has theoretically been valid for two millennia, to retain its validity until the present day.
For mathematicians we must add that this curve is approximated well by the real-analytic functional relation as a solution of an analytic problem of celestial mathematics. Therefore, the fact that it demonstrates strict periodic behaviour within a certain interval implies that it should behave with similar periodicity on the entire real number line. In other words, it should remain periodic in the closest future as well.
What do we see in reality? Let us return to fig. 5.7. If Comet Halley continued to move in accordance with its centenarian, allegedly periodic, recurrence interval fluctuation law, the real curve of these intervals would have moved in the direction of Cowell and Crommelin’s dotted line after 1759, or manifest growing recurrence intervals. However, we find the reverse to be the case in reality.

Fig. 5.10. Breaks in the false periodicity of Comet Halley’s behaviour discovered in the XX century. This fact delivers a mortal blow to the Scaligerian chronology of Comet Halley observations that follows the “ancient” Chinese chronicles.
This is especially obvious in fig. 5.10. The thick black curve corresponds to the behaviour of Comet Halley’s recurrence intervals in the years of 1759, 1835, 1910 and 1986. This curve completely disproves the “Chinese experimental law”, which is said to have remained valid for two millennia.
Apparently, N. A. Morozov was the first one to doubt the validity of this “periodic law”. His commentary is as follows:
“The comet appeared in 1910, forestalling the predicted date by 3.5 years. This fact gives us a reason to suspect a certain arbitrariness in the selection of mediaeval dates as well, possibly aimed at validating the sine curve of accelerations and decelerations” ([544], Volume 6, page 138).
Several decades later, when Comet Halley reappeared earlier than it was predicted by the “Chinese law”, we can assert it with even greater confidence that the consensual chronology of Comet Halley’s recurrence contains grave errors.
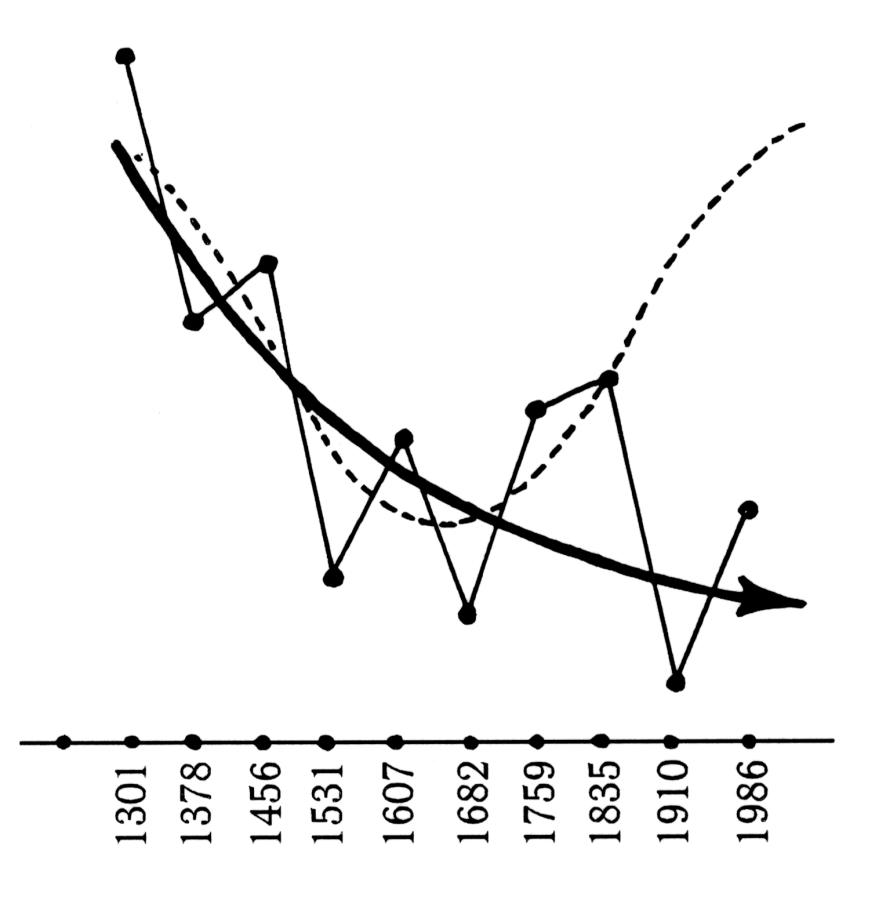
Fig. 5.11. The real behaviour of Comet Halley over the last six hundred years drawn as a thick curve. The dotted line demonstrates how Comet Halley should have behaved in accordance with the false periodic law of the “ancient” Chinese records. Similarly to the previous graphs, the dates of Comet Halley observations are on the horizontal line, and the intervals between observations are on the vertical line.
Fig. 5.11 shows the behaviour of Comet Halley’s recurrence intervals over the course of the last six hundred years, that is, between 1301 and 1986 A. D. Since we can more or less trust the Scaligerian chronology of this time interval, it makes sense to assume that fig. 5.11 corresponds to the real behaviour of Comet Halley, on the condition that its apparitions in the XIV-XV century A. D. were identified correctly in the Chinese and European records. However, we have already mentioned that we have every reason to doubt the correctness of such identifications – otherwise, why would the trajectory of the comet observed in 1378, conditionally identified as Comet Halley, confuse the astronomer Pingré so much (see above)?
However, let us agree with Scaligerian chronology for the time being and assume that every apparition of Comet Halley over the course of the last six centuries was identified in the respective Chinese and European observations correctly.
What do we see? The approximated curve of time intervals, represented as a thick black line in fig. 5.11, obviously recedes, which implies the reduction of Comet Halley’s recurrence intervals on the average. It is perfectly obvious that the dotted line that represents the hypothetical “Chinese law” of Cowell and Crommelin does not correspond with the real apparitions of Comet Halley over the course of the last six hundred years.
In other words, the comet is sighted in the vicinity of the Sun more and more often. The reasons behind this tendency remain somewhat unclear – Comet Halley’s orbit might be affected by substantial fluctuations, and it may be accelerating. It is possible that it is beginning to disintegrate on the whole. Only its future sightings can shed some light over the issue – as of this moment, we haven’t got enough data to predict its evolution.
However, one can make the more or less definitive claim that every reappearance of the comet reveals substantial changes in its behaviour, which means that there are no reasons whatsoever to assume that its past apparitions were characterised by any periodicity at all.
This leads us to a very important conclusion. Taking into account all the above considerations, we must admit that the “Chinese saw-tooth curve” as the presumed recurrence cycle function of Comet Halley is manifestly false. It cannot possibly reflect the real sightings or the real trajectory of the comet. Therefore, it is either of a random nature, or a forgery, all in all, either premeditated or unwilled and resulting from “the very best intentions”. We shall discuss this issue below.
5.2.4. The provenance of the “Chinese law of periodicity” for Comet Halley.
We may be asked the following question, which is perfectly justified: if the behaviour of Comet Halley does in fact lack periodicity, whence did the experimental saw-tooth curve that provided Cowell and Crommelin with a foundation for their hypothesis actually originate? After all, they did manage to locate every single dot of the graph in the old comet rosters, and arrange them into the “Chinese law of periodicity” perfectly well. Could all the Chinese observations have been counterfeited in order to prove the periodicity of Comet Halley’s recurrence cycles over the course of the last two thousand years? One cannot deny the fact that the graph in fig. 5.7 contains at least 17 dots that represent the pre-XIV century epoch. Is it possible that each and every one of them is the result of a forgery?
This is not the case, obviously enough. However, our analysis demonstrates that a partial forgery did actually take place; simultaneously, as we shall demonstrate in an instant, it was unnecessary to fabricate several dozen records. The structure of the Chinese comet roster, dense as it happens to be, is such that the substantiation of almost any “law of periodicity” would require the fabrication (insertion) of three observations maximum.
Let us linger upon this for a while.
The matter is that the Chinese comet roster is exceptionally dense – in other words, it contains a great variety of recorded “comet sightings”. Let us assume that someone might pursue the objective of integrating a certain “law of periodicity” into it, which comes down to the task of discovering a periodic series of observations separated by equal intervals of 76 years, 80 years, 120 years etc. Is it feasible at all?
Actually, yes. Moreover, it is possible to implement this for almost any given periodicity value – we can find a “comet” with the recurrence cycle of 55 years, 101 years and so on. However, in some cases ideal periodicity will require the insertion of two or three observations into the comet roster. Interval values that would complicate the formulation of such a “periodicity law” due to the necessity of adding too many “observations” to the roster are few and far between.
Let us begin our demonstration with the observation of Comet Halley that dates from 1607, which is located at the very end of the Chinese roster. We believe this record to be veracious – after all, it dates from as recent an epoch as the XVII century.
We have tried to find a fitting observation for every prior date covered by a step with a fixed value. It turns out that the majority of such a priori defined interval values shall correspond to actual observations contained in the Chinese comet rosters with the maximal precision margin of three years, with no more than three lacunae for the entire roster, qv in the table below.
Therefore, the insertion of an observation or two into the Chinese cometary roster suffices to use the latter for the validation of any centenarian periodicity law for Comet Halley – moreover, any recurrence cycle can be substantiated in this manner quite as easily. Exceptions are extremely rare – there are very few actual “unfortunate” periodicity values that completely fail to correspond with the Chinese experimental data.
Comet Halley has got nothing to do with these matters – the sole reason is the extremely high chronological density of the Chinese comet roster, which makes it possible to discover any kind of periodicity in the motion of any comet.
Let us cite the table of correspondence between different “periodicity values” of Comet Halley’s apparitions and the “experimental” Chinese data for the period between 100 B. C. and 1607 A. D.
The first column of the table contains the value of the “period” – we have tried every value in the range between 50 and 200 years, calculating all possible discrepancies (in years) between the “theoretical” dates of Comet Halley’s repeated sightings in the past as determined for this “period” and the most fitting “experimental” dates from the Chinese comet roster for each of said values. The resulting discrepancy values were then arranged in the order of decreasing and marked d1, d2, d3 etc. The first four values of this decreasing (or, rather, non-ascending) sequence can be found in columns 2-5 of our table.
Thus, the second column contains the maximal value of discrepancy (in years) between the “theoretical” sightings of Comet Halley in the past calculated for a given “period” and the best matches from the Chinese comet roster. The third column contains the second greatest discrepancy value. The fourth and the fifth are ascribed to the next two values in descending order. Thus, we indicate the four greatest discrepancy values for a given “period”, which represent the difference between the Chinese data and the periodicity law of Comet Halley’s recurrence cycles as formulated for the “period” in question.
TABLE.
A comparison of the Chinese comet data and the “theoretical” reappearances of Comet Halley as calculated for randomly chosen recurrence periodicity values.
The comparison covers the interval between 100 B. C. and the end of the Chinese comet roster.
_______________________________________________________________
Period d1 d2 d3 d4
value
_______________________________________________________________
50 15 7 3 1
51 23 10 4 1
52 31 8 1 1
53 32 4 4 1
54 24 6 1 1
55 16 5 2 2
56 14 10 3 0
57 16 14 7 4
58 21 5 4 0
59 28 11 3 0
60 35 7 3 3
61 29 6 5 1
62 22 9 7 0
63 22 15 15 11
64 13 8 8 8
65 10 7 5 5
66 16 11 3 3
67 17 17 5 1
68 23 4 1 0
69 29 7 1 1
70 35 10 6 1
71 30 12 8 3
72 24 7 4 1
73 18 2 0 0
74 20 12 2 1
75 19 9 6 3
76 16 11 5 5
77 3 3 2 2
78 14 10 6 6
79 10 2 2 1
80 15 6 2 2
81 22 20 6 3
82 25 2 2 0
83 30 2 2 2
84 35 6 1 0
85 31 3 2 1
86 26 2 2 0
87 25 21 5 5
88 16 9 3 1
89 11 11 2 0
90 18 7 3 3
91 15 5 5 5
92 10 7 7 5
93 10 9 9 6
94 22 11 7 0
95 16 10 6 0
96 9 8 5 0
97 7 6 4 0
98 8 7 7 7
99 14 11 3 2
100 15 3 1 0
101 19 2 0 0
102 23 4 1 0
103 27 6 2 0
104 31 8 1 0
105 35 6 0 0
106 32 4 4 1
107 28 7 2 0
108 24 6 0 0
109 20 3 1 1
110 16 2 0 0
111 12 3 1 0
112 14 8 6 2
113 24 6 4 4
114 16 11 6 5
115 13 5 3 2
116 20 8 5 1
117 15 8 0 0
118 11 2 1 0
119 10 2 0 0
120 8 7 3 0
121 14 4 4 4
122 8 7 7 5
123 7 6 0 0
124 10 7 0 0
125 19 8 0 0
126 22 9 0 0
127 13 8 0 0
128 8 7 0 0
129 12 6 6 0
130 10 7 5 5
131 10 8 5 4
132 11 3 3 0
133 14 2 0 0
134 17 1 1 0
135 20 0 0 0
136 23 2 1 0
137 26 4 2 0
138 29 6 1 0
139 32 8 0 0
140 35 10 1 0
141 33 10 1 0
142 30 8 0 0
143 27 6 1 0
144 24 4 1 0
145 21 2 0 0
146 18 0 0 0
147 15 1 0 0
148 12 2 1 0
149 9 4 0 0
150 6 3 0 0
151 10 6 3 1
152 11 4 1 1
153 5 3 1 1
154 3 2 0 0
155 10 10 3 2
156 14 6 6 2
157 7 4 3 0
158 5 4 2 0
159 10 4 4 1
160 14 8 8 6
161 21 13 8 2
162 22 18 6 1
163 19 8 4 0
164 14 5 5 2
165 9 9 4 2
166 5 4 4 2
167 4 4 1 0
168 8 6 0 0
169 5 1 0 0
170 7 3 3 2
171 8 5 3 0
172 8 7 4 2
173 7 3 1 0
174 5 5 0 0
175 7 7 0 0
176 9 9 0 0
177 11 0 0 0
178 11 1 0 0
179 9 2 0 0
180 7 3 0 0
181 11 5 5 4
182 14 10 5 5
183 8 8 6 0
184 10 7 0 0
185 8 0 0 0
186 10 9 0 0
187 16 10 0 0
188 22 11 0 0
189 22 11 0 0
190 16 10 0 0
191 11 9 0 0
192 8 0 0 0
193 7 7 0 0
194 7 6 0 0
195 8 5 5 5
196 8 7 4 0
197 9 3 0 0
198 11 2 0 0
199 13 1 0 0
200 15 0 0 0
Consider the last column of the table. More than half of the values contained therein are zeroes. Only ten per cent of discrepancy values exceed three years.
Thus, in 90 per cent of all cases the Chinese comet roster will “confirm” a given arbitrary period value to be the alleged “recurrence cycle value” of Comet Halley, and with high precision at that – the maximal discrepancy value shall not exceed three years in any of the cases. In fifty per cent of the cases the “correspondence” shall be ideal. The greatest number of lacunae in the Chinese roster, by which we mean a lack of correspondence with the “theoretically calculated” date in a given instant, does not exceed three.
Indeed, what do we mean if we say that the fourth largest value of discrepancy between the Chinese experimental data and the “theoretically calculated” equivalents does not exceed three years? It means that no other “theory vs. experiment” discrepancy value (with the sole possible exception of the first three values found in columns 2-4) exceeds 3 years, either.
Hence the theoretical “excellent correspondence between the theory and the experimental Chinese data”. The structure of the Chinese comet roster provides for such “excellent correspondences”, regardless of whether or not the theory in question is correct.
Let us return to our table. As it is easy enough to see, one of the theoretically possible “Comet Halley recurrence period values” stands out distinctly – namely, that of 77 years. It is made unique by the fact that nearly every single alleged sighting of Comet Halley corresponding thereto is actually represented in the Chinese roster. Initially, it strikes us as indubitable proof of veracity that validates the roster itself, the dates it contains and the “Comet Halley Theory” in general.
However, this is just the initial impression. Indeed, the last advent of Comet Halley in 1986 could not be observed from the Northern Hemisphere.
Could this be the only such case in seventeen hundred years? This fact alone makes the “ideal correspondence” between the theory and the “Chinese experiment” highly suspicious.
Let us point out that the European comet roster, which has an even greater density than its Chinese counterpart, does not contain any quintuple recurrences of Comet Halley, qv above. Therefore, the European roster does not confirm the periodicity of Comet Halley’s recurrence. Actually, a more precise formulation shall ring as follows: the periodicity of Comet Halley’s recurrent observations does not confirm the veracity of the European comet roster.
As we have demonstrated, the discrepancies between the “Chinese experiment” and the theory (with a period equalling 77 years) are also far from random and can be expressed as a saw-tooth curve, qv above. The sum total of these circumstances leads us to the conclusion that what we have before us is clearly a case of forgery.
5.2.5. Dating the introduction of fabricated data into the “observation records” of Comet Halley.
The dating in question is easy enough to estimate. It suffices to take a look at the curve in fig. 5.7 and mark the point where the strict periodicity in the behaviour of the saw-tooth curve built for Comet Halley ceases to manifest. This occurs on the interval between 1759 and 1835. In other words, to the left of the 1759 mark, the saw-tooth curve spawns two or even three copies of itself, which are almost completely identical to one another. What we see is the allegedly ideal “centenarian periodicity law”.
In 1835 this “law” gets broken for the first time, qv in fig. 5.7. Although this very first discrepancy is far from catastrophic, it is nonetheless clearly manifest – the first time in two thousand years. However, since the first discrepancy was rather mild, it is easy enough to understand Cowell and Crommelin, who didn’t consider it a deviation from their “Chinese periodicity law” of Comet Halley’s recurrence.
However, the next two advents of Comet Halley (in 1910 and in 1986) were completely outrageous from this theory’s point of view. One must think that if Cowell and Crommelin were our contemporaries, they wouldn’t merely refrain from advertising their discovery of the “Chinese law”, but also put the chronology of the Chinese comet rosters to question, just as we have done.
It goes without saying that the missing observations (three of them at most) weren’t introduced in the Chinese roster by Cowell and Crommelin, eager to build an ideal sine curve. They merely processed the Chinese rosters available at their time and made rigid by the tradition.
A visual study of the “Chinese curve” leads us to the assumption that the insertion of fabricated observation records (a maximum of three) must have taken place between 1759 and 1835. This is the only condition upon which the law in question could have been formulated with “immaculate precision” – before the embarrassing observation of 1835, which wasn’t taken into account by the authors of the forgery. Therefore, the forgery must predate 1835; however, it is also most likely to postdate 1759.
But how can this be true? Weren’t the Chinese comet rosters published by Mailla and Gaubil in the XVII century (see above)?
The reply is as follows. Indeed, the initial version of the Chinese rosters must have been published in the XVII century. However, in the beginning of the XIX century more detailed versions of the Chinese rosters came out – one of them was published by Biot in 1846, for instance ([544], Volume 6, page 42). This curious fact had already been pointed out by N. A. Morozov, who never managed to find out anything about the origins of these mysterious supplements to the Chinese roster of the XVII century.
However, nowadays we realise that if the supplements in question were introduced in the beginning of the XIX century, shortly before the publication of the new extended Chinese roster, this circumstance is in good concurrence with our reconstruction. The initial Chinese roster was complemented with a few “observations” designed to justify the “Chinese sine curve” of Comet Halley.
One shouldn’t consider the parties responsible for said forgery malevolent falsifiers. They must have been guided by the best intentions possible. The matter is that the approximate recurrence cycle of Comet Halley must have already been known – possibly calculated in the epoch of Halley, or the XVIII century, on the basis of three or four real observations of the comet made in the XVI-XVIII century.
Scientific thought was evolving, and somebody must have come up with the brilliant idea of looking for the recurrent observations of Comet Halley in deep antiquity as reflected in the stupendous Chinese rosters dating from times immemorial. We are of the opinion that this person wasn’t that much au fait with astronomy.
For some reason, this mysterious well-wisher decided that the duration of the comet’s recurrence period had always fluctuated around the average value of 77 years. The next step involved the construction of a graph spanning the last seven or eight hundred years, which was then mechanically copied so as to reach further back into the past. The resulting graph turned out a periodic saw-tooth curve. The author must have been overjoyed at finding almost all of the required dates included in the graph, failing to understand that any other value of the recurrence period would have yielded the same results (109 years instead of 77, for example).
Let us repeat that the author must have been ill at ease with astronomy. The two or three observations aimed at the “justification” of his “theory” must have been lacking from the roster. This dissonance between the theory and the practice, which would be perceived as normal by a professional astronomer, transformed into a menace to the harmonious model of the author’s newly created paradigm, hence the decision to introduce the missing observation (alternatively, the author could have found some Chinese document and interpreted the vague data and evidence contained therein in the desired key). The motivation behind this must have been pure and noble, such as the desire to reconstruct the veracious picture of the distant past.
Some 100-150 years later, Cowell and Crommelin, two professional astronomers, made the astonishing discovery of this recently created graph. They transformed it into an astronomical “law of nature”, effectively canonising this artificial construction. Shortly afterwards, in 1910, this law was ruthlessly broken by nature itself when Comet Halley appeared in the sky 3.5 years earlier than the “Chinese graph” had predicted.
All of this activity must have resembled the mediaeval Cabbala, or the attempts of many scientists to find harmonious and perfect numeric relations in nature – the great Kepler descanting universal harmony is a good example. It was particularly vogue to calculate lunar eclipses, horoscopes and the like into the past; apparently, comets weren’t spared this fate.
Let us conclude with another observation concerning the 77-year recurrence period of Comet Halley. If we are to consider the entire Chinese comet roster and not just the part of it that postdates 100 B. C., as we have done above, the 77-year period value ceases to be unique as compared to all the other possible values. It lacks two dots for ideal repetition, likewise many other period values.
5.2.6. On the chaotic character of Comet Halley’s motion.
In 1989, B. V. Chirikov and V. V. Vyacheslavov published an article in Astronomy and Astrophysics ([1066]). They demonstrate therein that the motion of Comet Halley is largely affected by a random compound. This work was brought to our attention by Professor V. V. Kozlov, Member of the Russian Academy of Sciences, Professor of the MSU and Doctor of Physics and Mathematics, as well as A. I. Neyshtadt, Professor of the MSU and Doctor of Physics and Mathematics.
The main corollary of the authors’ research can be formulated as follows: “It was demonstrated that the motion of Comet Halley is chaotic due to the perturbations caused by Jupiter” ([1066], page 146).
Therefore, the model of Comet Halley’s motion is by no means determinate, but rather constructed within the paradigm of dynamic chaos – in other words, if a certain comet, such as Comet Halley, for instance, revolves around a greatly elongated orbit that reaches beyond the circular orbit of Jupiter, it meets the latter in a random phase every time it returns to the Solar System due to the incompatibility of their revolution periods. Jupiter, being a massive planet, affects the perturbation of the comet’s trajectory the most. Thus, upon encountering the planet in a random phase, the comet becomes subjected to a random perturbation.
Apparently, comets of this kind (as described by the mathematical model developed in [1066]) are characterised by chaotic dynamics. One of the most sensitive parameters of a comet’s orbit is the time of its passage through the perihelion, or the time it takes a given comet to return (its period). In particular, the period of Comet Halley is a random value with an exponentially progressive dispersion.
However, the “ideal Chinese sine curve” could not have become manifest in the behaviour of Comet Halley as a result of a random experiment.
Our opponents may appeal to the theoretical possibility of miracles, their scarcity notwithstanding. We do not deny it – for instance, a monkey pressing the keys of a typewriter might produce a coherent text without any grammatical errors (a novel, for instance). However, the probability thereof is negligibly small, although it doesn’t equal zero. The same is true about the possibility of the “Chinese curve” being the product of a random experiment series. The probability thereof is just as small and just as negligible as the chance that some monkey might type the entire text of “War and Peace” with gusto and élan – all four volumes of it, sans errors or omissions.
5.2.7. Suspiciously high frequency of improbable occurrences in Scaigerian history.
It would be apropos to make a general observation concerning historical events of low probability. N. A. Morozov, likewise the authors of the present book, would often encounter the following sort of counter-argumentation. Let us quote from one of Morozov’s most qualified opponents as an example – B. A. Rosenfeld, a mathematician and the author of the article entitled “Mathematics in the works of N. A. Morozov” ([583], pages 129-138). B. A. Rosenfeld wrote the following in re the numerous bizarre parallels inherent in the traditional version of history, such as coinciding reign durations characteristic for the dynastic currents from different epochs, recurrent astronomical events and so forth:
“Morozov would calculate the probability rates of various events; upon finding them infinitesimal, he would declare such coincidences impossible. Considerations of this sort are completely invalid [? – Auth.], seeing as how the probability theory is concerned with mass events and not individual ones. Events whose probability rates approximate zero to whatever extent can still actually happen” ([583], page 137).
The last claim of B. A. Rosenfeld is actually true. Events with infinitesimal probability rates do happen – however, if one is to make a certain improbable event happen, one needs to run a large number of trials – more precisely, its magnitude needs to be inversely proportional to the value of the probability rate. Therefore, apart from the actual probability rate of a given event, one also needs to consider the amount of trials required for this event to happen.
There is a special discipline concerned with these very matters – it is called mathematical statistics. And one must state that N. A. Morozov’s considerations are perfectly valid insofar as mathematical statistics is concerned.
If we are to explain the above on the qualitative level to the lay reader, we must point out that the objections along the lines of “the event is improbable, but it could still have happened randomly” that we hear so frequently cannot be voiced too often – once or twice, three times at most. They are also applicable to individual occurrences and nothing but; as soon as they get voiced too often and become applied to whole series and classes of improbable coincidences inherent in the traditional version of history, they become utterly meaningless.
Some of our readers might voice the very same sentiment in re Comet Halley and the allegedly random nature of the Chinese curve, whose probability rate is minute but yet greater than zero, which makes it possible.
However, this sentiment will be nothing but yet another link in a lengthy chain of similar objections. Scaligerian history is virtually packed with events with probability rates approximating zero. Each objection of the above sort only makes sense as an individual phenomenon – as soon as it becomes drowned in a multitude of similar objections, the entire multitude loses all validity and meaning.
Let us emphasise the following important circumstance once again. Why do all such “mass-produced coincidences” precede the XVI century A. D. chronologically? Why have they been nonexistent for the last four hundred years? What is the matter with history – how come it has only been conforming to the rules of the probability theory for the last four hundred years, after having stubbornly ignored the laws of mathematical statistics for centuries on end?
5.3. In re the comet of Charles V.
The famous comet of Charles V is a spectacular example of how the Chinese comet roster can be used to prove virtually anything. The comet in question appeared in 1556, “it was large, and the Chinese describe it similarly. 292 years before it, in 1264, a similar comet was observed right before the death of Pope Urban – it is also recorded in the ‘Annals’ (She-Ke). Pingré used this source to estimate the comet’s orbit as extremely similar to the orbit of the comet of Charles V . . . He identified both comets as one and the same comet, whose recurrence cycle equals 292 years. This theory stipulated the search of the same comet in 972, 680, 388 and 96 A. D.” ([544], Volume 6, pages 157-158).
Needless to say, scientists managed to find all the necessary dates in the Chinese roster; the European roster also contained all of them save for the first one. Once again, there is nothing surprising about this fact whatsoever – the comet rosters are very dense, and the descriptions they contain are vague enough to suit any taste identification-wise.
N. A. Morozov was perfectly write to note: “Everything seems to be perfectly harmonious here, just as it is in case of Comet Halley: Chinese and European sources alike ‘confirm’ the periodicity of the comet of Charles V, and the actual comet of Charles V, in turn, confirms the veracity of these records traced back to the beginning of the new era . . . However, the expectants were soon disappointed in the most deplorable manner – when they tried to foretell its return around 1858, it mocked their expectations by never turning up . . . it hasn’t been observed to date, which was truly a blow to all of the ‘validations’ contained in the Chinese annals” ([544], Volume 6, page 159).
What we see is yet another example of insufficiently justified attempts of employing the dense Chinese and European rosters in order to validate the periodicity of comets. Such attempts are made for one reason only – astronomers trust these rosters too much, being unaware of the fact that the rosters in question may in fact be of a very recent origin. Moreover, the very density of records contained in comet rosters, which confuse real observations of comets with their duplicates multiplied in various chronicles, allows to use them for the “validation” of virtually anything.
5.4. Strange duplicates with the periodicity of 540 years inherent in the Chinese and European comet rosters.
N. A. Morozov discovered the following strange tendency that characterises all known comet rosters, European as well as Chinese, in the course of his analysis related in [544], Volume 6. All the ancient comets that predate 59 A. D. recur over the period of 540 years. Moreover, the large lacunae, or gaps in comet observation records, recur after the same period of time.
He wrote the following: “This is by no means a random occurrence; therefore, only two explanations are possible” ([544], page 167).
The first one: the “ancient” comets copy more recent ones.
The second: the real astronomical life of comets has a strange 540-year period, which makes all comets “recur” after the passage of 540 years.
N. A. Morozov adds that a third explanation is also possible; we believe it to be the closest to the truth. A shift of 540 years “is also possible if the historical events associated with the sightings of all the European comets were shifted backwards in time by a factor of 540 or 1080 years” ([544], Volume 6, page 170). However, the shifts of 540 and 1080 years are known to us quite well – they are indeed manifest in the Scaligerian version of the “ancient” history and can be discovered by a variety of independent methods – statistical, astronomical etc. We discuss them at length and in great detail above.