CAPITOLO 2
L’analisi preliminare del catalogo stellare dell’Almagesto
7. Le versioni della densità come la densità delle osservazioni stellari indipendenti.
Le sette aree dell'atlante stellare dell'Almagesto rivedute in base alla nuova concordanza con i risultati precedenti.
Per poter trarre delle conclusioni dalla Tabella 2.4, dobbiamo eseguire una semplice operazione aggiuntiva, vale a dire calcolare la quantità media delle versioni delle coordinate stellari per tutte e sette le aree di “precisione variabile” sulla carta astrale dell'Almagesto elencate sopra. Per questo scopo divideremo le file delle ultime due colonne della Tabella 2.4 in sette gruppi (A, B, M etc..) e poi calcoleremo la media dei valori di ogni singolo gruppo. Il risultato è stato presentato nella Tabella 2.5. La quarta riga della tabella fornisce la base per la Figura 2.21 e mostra la percentuale delle informata per ogni regione celeste. Le ultime due righe della Tabella 2.5 sono le più importanti. La quinta riga mostra la versione della densità tenendo conto delle molteplicità, mentre la sesta fornisce le stesse informazioni senza le molteplicità, ossia le ripetizioni. Per una rappresentazione ancor più dimostrativa dei dati, passiamo alla Figura 2.22. La linea orizzontale contiene numeri delle costellazioni dell'Almagesto raggruppate nelle sette aree della carta astrale, vedi la Figura 2.17. Nella linea verticale possiamo vedere la quantità media delle versioni per ognuna di queste aree.
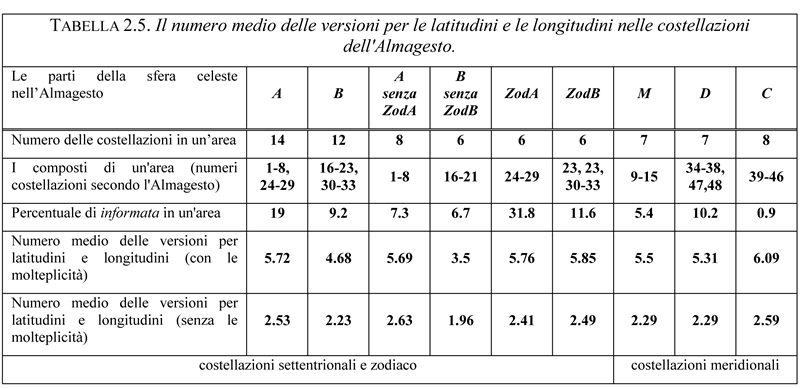
La Tabella 2.5 e la Figura 2.22 ci portano ai seguenti corollari:
Corollario 1. Il grafico della versione della densità con le molteplicità concorda bene con quello senza. Ciò implica che i modelli logici elencati di seguito si manifestano in entrambi i grafici. Vi facciamo notare che il grafico della densità senza le molteplicità ha minori fluttuazioni di amplitudine rispetto al grafico della densità che tiene conto delle molteplicità. Questo è abbastanza ovvio: dal momento che uno le include, le fluttuazioni di densità possono essere osservate in modo più realistico. La Figura. 2.22 mostra proprio questo.
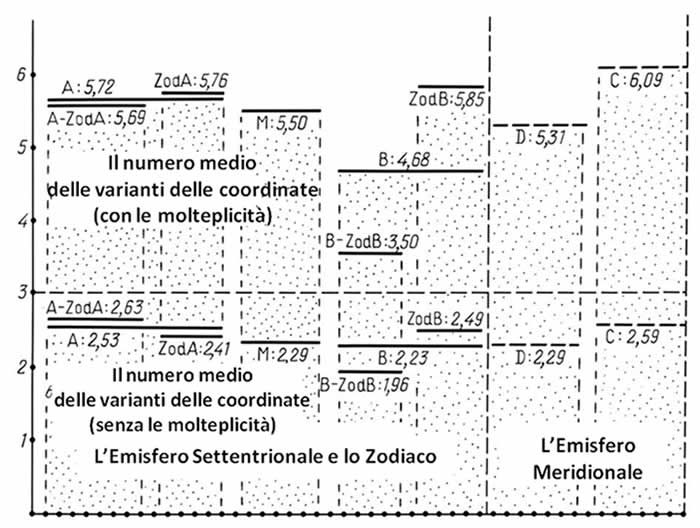
Figura 2.22.
La distribuzione della densità per i numeri delle versioni delle coordinate stellari nel catalogo dell'Almagesto. Le densità sono state indicate con e senza le molteplicità.
Corollario 2. La densità delle coordinate astrali sull'atlante stellare dell'Almagesto concorda perfettamente con la distribuzione delle stelle identificate con affidabilità nelle costellazioni “pure” dell'Almagesto, come pure con la distribuzione della densità delle informata.
Riportiamo le informazioni che riguardano la distribuzione di dette densità in quattro tabelle: 2.6, 2.7, 2.8 e 2.9. La Tabella 2.6 mostra la distribuzione delle stelle identificabili con sicurezza nelle costellazioni pure dell'Almagesto. Le righe e le colonne della tabella corrispondono alle seguenti regioni che abbiamo scoperto sulla carta stellare dell'Almagesto: A, B, A meno Zod A, B meno Zod B, Zod A, Zod B, M, D e C. Le ultime tre colonne e righe della tabella si riferiscono alle aree dell'emisfero australe.
Le celle della tabella contengono i segni + e - (o, in alcuni casi, + = / - =). Il loro significato è il seguente. Ad esempio, consideriamo la prima fila della tabella che corrisponde all'area A. La rispettiva percentuale è maggiore per l'area A che per l'area B; pertanto, mettiamo un + nella cella che incrocia la prima riga e la seconda colonna. Inoltre, la percentuale è formalmente maggiore per l'area A che per A meno Zod A, ma di fatto è uguale a quest'ultima; pertanto, mettiamo un segno += nella rispettiva cella; se questa percentuale si dimostrerà minore, useremo -; se dovesse essere minore ma di fatto uguale.
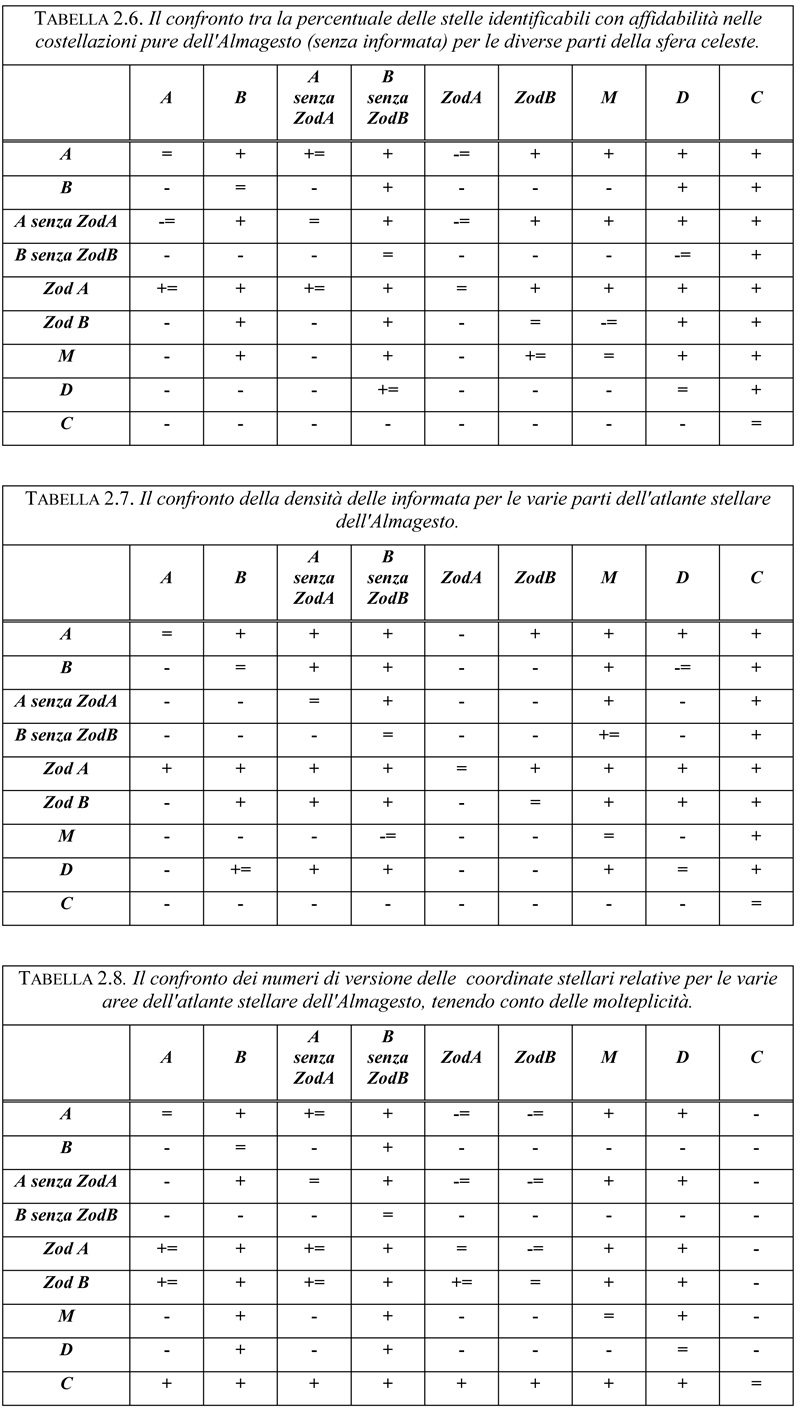
L'implicazione è che quando osserviamo la Tabella 2.6, possiamo tranquillamente dire in modo affidabile che la percentuale delle stelle ben identificabili è comparativa per ogni coppia di aree. La Tabella 2.6 è una rappresentazione compatta della distribuzione della densità in tutte le aree della carta stellare sopra descritta.
Le successive tre tabelle si basano sullo stesso principio. La Tabella 2.7 mostra la densità di distribuzione delle informata nell'atlante stellare dell'Almagesto, mentre la Tabella 2.8 ci dà l'opportunità di confrontare la densità delle versioni delle coordinate stellari dell'Almagesto per le diverse aree celesti. Le versioni che formano questa tabella sono state calcolate con le molteplicità, il che significa che se la stessa versione venisse rilevata più volte, l'intero importo aumenterebbe di conseguenza. Se volessero escludere le molteplicità, ossia contare semplicemente ogni versione alla volta, il risultato sarebbe una presentazione comparativa della quantità delle versioni delle relative coordinate per le diverse aree dell'atlante stellare dell'Almagesto, vedi la Tabella 2.9.
Le tabelle 2.6-2.9 rendono ovvio che la distribuzione dei più e dei meno è praticamente uguale, il che implica una buona correlazione tra i seguenti quattro valori:
- la percentuale di stelle identificabili con affidabilità in una data area della carta stellare dell'Almagesto;
- la densità delle informata nell'area in questione della carta stellare dell'Almagesto;
- la densità delle versioni delle coordinate stellari con le molteplicità;
- la densità delle versioni delle coordinate stellari senza le molteplicità.
In particolare, maggiore è la densità di informata e la densità della versione delle coordinate in una determinata area, più affidabile sarà l'identificazione delle stelle situate in essa.
L'implicazione è che non possiamo interpretare le versioni delle coordinate presentate nei 26 manoscritti dell'Almagesto, esclusivamente come errori degli scribi. Se fosse stato questo il caso, ci avrebbe portato a priori a formulare delle false affermazioni che la crescita del tasso di errore in una determinata area si traduce in una migliore identificazione della stella. Dobbiamo quindi respingere l'ipotesi che questa abbondanza di versioni sia attribuibile alla noncuranza degli scribi. In questo caso, l'unica spiegazione ragionevole dell'effetto scoperto può essere spiegata come segue.
La moltitudine delle diverse versioni di coordinate stellari nei manoscritti dell'Almagesto risulta essere indipendente dalle osservazioni stellari eseguite più volte da un osservatore o da un gruppo di osservatori. A causa dell'imprecisione degli strumenti utilizzati per queste osservazioni, i risultati differiscono spesso l'uno dall'altro. Più erano le misurazioni delle coordinate di una determinata stella, più erano le versioni che venivano messe nei manoscritti. Pertanto, le aree della carta stellare con un'alta densità di versione delle coordinate sono quelle le cui stelle furono osservate più volte e le cui coordinate vennero misurate di nuovo; in altre parole, queste aree beneficiarono maggiormente dell'attenzione dei ricercatori rispetto alle altre. È ovvio che se a una determinata regione celeste veniva prestata più attenzione, più affidabili erano le identificazioni delle stelle che conteneva. Come dimostreremo nei capitoli successivi del nostro libro, le coordinate di quelle stelle furono effettivamente misurate molto meglio della media per l'epoca di Tolomeo.
Pertanto, se volessimo semplificare un po' la situazione, ci sarebbero le ragioni per presumere che i 26 manoscritti fondamentali dell'Almagesto sono in gran parte delle “bozze”, piuttosto che delle copie meccaniche. Successivamente vennero utilizzati per la creazione del testo canonico finale. La versione di Scaligero sull'origine di questi manoscritti non concorda con le nostre conclusioni. Infatti, perché gli scribi medievali avrebbero copiato per secoli delle “bozze” insieme alla “versione finale”? Sarebbe molto più sensato presumere che entrambi risalgano approssimativamente alla stessa epoca e che il numero delle copie era tutt'altro che grande. Ribadiamo che le osservazioni eseguite in questo modo non saranno utilizzate nella nostra ricerca; sono solo un mucchio di domande che nascono spontaneamente e che vogliono dimostrare le diverse possibili spiegazioni dell'effetto che abbiamo scoperto, niente di più.
Infine, riportiamo la Figura 2.23 dove uniamo tutti i suddetti grafici della distribuzione della densità in uno. La dipendenza tra i vari grafici è ovvia.

Figura 2.23.
Grafico in cui si può vedere contemporaneamente quanto segue: 1) la distribuzione di qualunque percentuale di stelle identificate con affidabilità comprese nel catalogo dell'Almagesto; 2) la percentuale delle informata nelle varie aree della sfera celeste dell'Almagesto, 3) il numero medio delle opzioni delle coordinate stellari nei vari manoscritti dell'Almagesto, con le molteplicità, 4) il numero medio delle opzioni delle coordinate, senza le molteplicità. Si può ben vedere che, per quanto riguarda l'Emisfero Boreale, tutti e quattro i grafici della densità sono ben correlati tra loro.
8. In riferimento all’affidabilità delle misurazioni latitudinali e longitudinali contenute nell’Almagesto.
8.1. Secondo Robert Newton, le longitudini dell’Almagesto vennero ricalcolate da qualcuno; tuttavia questo sospetto non nasce fintanto che sono coinvolte le rispettive latitudini.
Cominciamo con il commentario fatto dall'astronomo R. Newton in riferimento alla precisione delle misurazioni nell'Almagesto. In linea generale, siamo del parere che le sue osservazioni siano applicabili a uno spettro di questioni molto più ampio. Newton ci fornisce davvero il resoconto molto diretto di uno scenario piuttosto meschino riguardo le letture e le interpretazioni di un gran numero di documenti astronomici “antichi”. Fa anche riferimento al “cosiddetto principio dell'immortalizzazione dell'errore”, che può essere formulato come segue. “Mettiamo che l'errore dell'autore A venga pubblicato e che un successivo autore B faccia in qualche modo riferimento ad esso ritenendo vera quella dichiarazione errata. Per cui l'errore viene immortalato nella letteratura scientifica e diventa impossibile cancellarlo. Si può difficilmente rimanere seri quando si viene a sapere che non esistono eccezioni per questa regola; tuttavia, ci sono un gran numero di esempi che seguono questo principio: è molto probabile che i lettori siano a conoscenza di parecchi di loro” ([614], pagina 165).
Sembra che stia accadendo qualcosa di simile con l'interpretazione scaligeriana dell'Almagesto, in particolare con la sua datazione. L'analisi della versione di Scaligero, che fa risalire il testo all'inizio della nuova era, necessita di un nuovo studio del suo contenuto. Si tratta di un problema scientifico complesso che richiede molto lavoro. Nella nostra ricerca eseguiamo una parte significativa di questo lavoro, per cui il lettore avrà l'opportunità di valutarne la complessità. La difficoltà principale è che bisogna arrivare proprio alle radici delle dichiarazioni e opinioni scientifiche in questione. Sembra che la stragrande maggioranza fu inizialmente fatta con il presupposto a priori o taciturno che l'Almagesto risalga ai primi secoli dell'era dopo Cristo. I nostri “scavi” avevano bisogno che il materiale di partenza venisse analizzato, cosa che richiese molto lavoro.
Torniamo ora al problema riguardo la complessità delle misure latitudinali e longitudinali. Nel Capitolo 1 abbiamo già spiegato che la natura stessa delle coordinate eclittiche ed equatoriali permette di misurare le latitudini in modo più sicuro delle longitudini.
Inoltre l'uso dell'armilla, ad esempio, può generare degli errori se l'astronomo crea un'inclinazione sbagliata dell'eclittica. La questione è che l'osservatore deve determinare l'angolo tra l'eclittica e l'equatore e quindi adattarlo per poter utilizzare uno strumento per la misurazione delle coordinate stellari: per esempio, deve regolarlo in conformità con l'inclinazione dell'eclittica trovata in precedenza. In generale, un'armilla può essere regolata con qualsiasi oggetto di cui si conosca la latitudine e la longitudine. Per questo scopo Tolomeo usava spesso la Luna. Ciò rende possibile calcolare le coordinate di qualsiasi altro oggetto che potrebbe interessarci. Tuttavia, come R. Newton ha fatto bene e far notare, in questo caso le imprecisioni nella determinazione delle coordinate dell'oggetto noto, portano automaticamente al calcolo errato delle coordinate del secondo oggetto ([614], pagina 151). Occorre anche tener costantemente presente che nel caso dell'Almagesto abbiamo a che fare con delle copie in cui i numeri sono stati trascritti come lettere, cosa che spesso causava confusione. Ad esempio, secondo gli astronomi R. Newton ([614], pagina 215), Peters e Knobel ([1339]), si poteva facilmente confondere le “antiche” cifre greche 1 e 4, a causa del fatto che la cifra 1 veniva trascritta come α e una delle sue vecchie forme ampiamente utilizzate erano molto simili alla lettera δ, che significava 4; da qui la confusione.
A questo riguardo occorre fare un'osservazione importante. La nostra ricerca si basa sulla versione canonica del catalogo stellare dell'Almagesto tradotta nell'opera di Peters e Knobel ([1339]). Come sottolinea R. Newton, “l'attento confronto dei vari manoscritti spesso rivela gli errori commessi nel processo della copiatura multipla e offre al ricercatore un'opportunità per correggerli. Peters e Knobel hanno studiato la Sintassi [Almagesto - autore] con la massima attenzione; è possibile che la loro versione del catalogo sia la più precisa di tutte” ([614], pagina 216).
Useremo anche l'analisi dettagliata eseguita dall'astronomo Robert Newton nell'enorme e speciale capitolo IX del suo libro ([614]), per valutare l'affidabilità delle longitudini e delle latitudini come indicate nell'Almagesto. Ometteremo i dettagli pertinenti all'analisi statistica condotta da R. Newton e citeremo semplicemente i suoi risultati.
R. Newton scrisse che “nel catalogo stellare, molto probabilmente le latitudini vennero misurate da un solo osservatore che impiegò un unico strumento” ([614], pagina 253). Inoltre: “le latitudini edotte dalle osservazioni furono inserite nel catalogo senza alcuna modifica (è comunque possibile che ci siano stati degli errori di trascrizione)” ([614], pagina 249). Secondo R. Newton, le latitudini del catalogo stellare dell'Almagesto sono un corpus di materiale abbastanza affidabile, ottenuto a seguito delle effettive osservazioni eseguite da Tolomeo o da uno dei suoi predecessori (Ipparco, per esempio). Questo concorda perfettamente bene con le informazioni citate sopra, le quali mostrano che le misurazioni latitudinali sono molto più semplici come procedura che quelle longitudinali; pertanto, la latitudine stellare è una coordinata misurabile in modo più affidabile.
L'immagine con le longitudini è drasticamente diversa. R. Newton afferma che “le longitudini non venivano dedotte da un qualunque tipo di osservazione ... i valori longitudinali venivano fabbricati” ([614], pagina 249). Inoltre: “la moltitudine delle longitudini contenuta nel catalogo stellare è altamente improbabile che sia stata determinata dalle osservazioni” ([614], pagina 250). Abbiamo già spiegato ai lettori che le misurazioni delle longitudini dell'eclittica si rivelano essere una procedura molto più sofisticata e complessa rispetto a quella delle latitudini. Inoltre, si presume che nel catalogo dell'Almagesto le longitudini vennero fornite nel 137 d.C. Questa interpretazione di una data scelta a priori è abbastanza semplice; tutto ciò che bisogna fare è aggiungere una qualche costante comune alle longitudini dell'eclittica di tutte le stelle. Questa costante è proporzionale alla precessione e dipende da quanto vecchie vuol far sembrare le longitudini il compilatore del catalogo. R. Newton è del parere che le longitudini originali ricavate sperimentalmente dall'antico osservatore, vennero successivamente ricalcolate di nuovo da qualcun altro. Questa è la sua soluzione fondamentale basata sull'analisi di quanto frequentemente compaiono i gradi delle frazioni nel catalogo: “Le longitudini vennero modificate. I risultati delle osservazioni furono aumentati di alcuni gradi e 40 minuti”([614], pagina 249). Questa operazione (l'aggiunta di un certo numero di gradi il cui valore potrebbe essere positivo o negativo, con un paio di frazioni) potrebbe far guadagnare o perdere al catalogo un'età considerevole, per volere del suo compilatore o falsificatore. Tenete presente che un'operazione del genere sarebbe stata del tutto impossibile con le latitudini o, per lo meno, molto più complicata. Tuttavia, se volessimo basare la nostra ricerca solo sull'analisi delle longitudini nelle copie esistenti dell'Almagesto, non potremmo determinare esattamente quanti gradi furono aggiunti o sottratti dalle longitudini iniziali. R. Newton sottolinea proprio la stessa cosa: “La distribuzione effettiva delle frazioni di grado non ci dice nulla su quanti siano stati i gradi aggiunti alla longitudine iniziale da Tolomeo” ([614], pagina 251).
A parte la semplice operazione di spostare tutte le lunghezze per il numero sconosciuto di gradi menzionato sopra, R. Newton ha scoperto le tracce di ricalcoli longitudinali più fini ([614], pagine 246-247). Pertanto, qualcuno aveva condotto un'ampia mole di lavoro nel ricalcolare le longitudini osservate inizialmente. Pertanto, l'elenco moderno delle longitudini che troviamo nell'Almagesto non rappresenta il vero materiale osservativo, ma è piuttosto un risultato scaturito da un'elaborazione piuttosto complessa, destinata ad aiutare a raggiungere un certo fine. Secondo N. A. Morozov, per esempio, questo fine potrebbe essere formulato nel fornire al catalogo una quantità arbitraria di età extra; in altre parole, ci troviamo davanti a una falsificazione. Tuttavia, ci asterremo a priori dal prendere le parti i qualcuno e analizzeremo le longitudini e latitudini sia insieme che separatamente.
Concludiamo con un'altra conclusione fatta da R. Newton: “Abbiamo un'immagine completamente diversa tramite le longitudini [rispetto alle latitudini - autore]. Non può essere data nessuna spiegazione plausibile alla distribuzione della frazione nella longitudine, indipendentemente che le osservazioni siano state eseguite o meno da una sola persona, che per lo scopo utilizzò un solo strumento” ([614], pagine 146-247).
8.2. Gli esempi i quali dimostrano che la datazione del catalogo stellare attraverso la precessione longitudinale spesso porta a grandi errori. I cataloghi medioevali cataloghi sono soggetti a essere erroneamente datati a un'epoca antidiluviana.
Per la datazione dei cataloghi, la versione scaligeriana dell'astronomia usa spesso il seguente metodo apparentemente semplice. Le longitudini dell’eclittica delle stelle di un vecchio catalogo vengono confrontate con quelle moderne. La differenza che ne deriva, che è all'incirca la stessa per tutte le stelle, viene quindi divisa per il valore della precessione, che equivale a circa 50 secondi all'anno o un grado in 70 anni. Ecco come gli storici determinano la rimanenza tra le date del catalogo moderno e quelle contenute nel vecchio. In particolare, questo metodo consente di “dedurre” le coordinate dell'eclittica dall'edizione del 1538 dell'Almagesto, in quanto sono uguali a quelle che corrispondono approssimativamente all'inizio dell'epoca dopo Cristo.
Tuttavia, il “metodo” sopra descritto sottointende l'implicazione che il compilatore del vecchio catalogo contava le longitudini dell'eclittica dal punto dell'equinozio primaverile della sua era, ossia nell'epoca in cui furono condotte le osservazioni stellari. Se fosse stato sempre così, il residuo risultante accumulato a oggi potrebbe davvero essere considerato il risultato della precessione. Supponendo che ciò sia vero, il metodo descritto sopra ci darebbe davvero la data approssimativa di creazione del vecchio catalogo. Tuttavia, è importante sottolineare che in effetti non era una caratteristica di tutti gli autori antichi, quella di usare il punto dell'equinozio primaverile della propria epoca come punto di riferimento iniziale.
Soffermiamoci per un po' su quanto detto sopra. Non si deve aver l'impressione che gli astronomi di un'epoca recente come il XVI-XVII secolo, calcolassero necessariamente le longitudini proprio nello stesso modo degli astronomi moderni. Parleremo ai lettori della famosa opera Cometography dell'autore medievale Stanislaw Lubienietski, pubblicata nel 1681: S. Lubienietski, Historia Universalis Omnium Cometarum ([1257]). Questo libro è noto per essere stato scritto nel XVII secolo. Elenca molte comete osservate fino all'anno 1680. Lubienietski apparteneva alla scuola degli astronomi del XVII secolo, per cui ha preceduto la nostra epoca di soli 300 anni. Diamo un'occhiata più da vicino al modo in cui Lubienietski calcolò le longitudini sulle sue carte stellari. Scopriamo che come meridiano celeste iniziale usò il meridiano che attraversava la stella γ dalla costellazione dell'Ariete, vedi la Figura 2.24. La “curva sinusoidale” che sta per l'equinoziale, ovvero l'equatore celeste in questa proiezione, qui viene direttamente indicato con “Aequator”, che è il mito che vediamo sopra gli alberi della nave degli Argonauti nella costellazione di Argo Navis, molto vicina all'estremità destra della mappa e ancora una volta vicina alla costellazione di Ofiuco in prossimità dell'estremità sinistra della mappa, vedi la Figura 2.24. L'eclittica è rappresentata da una spessa linea orizzontale divisa in gradi. Si può vedere perfettamente che l'eclittica e l'equatore si incrociano proprio dove si trova il confine della mappa, nella stella γ della costellazione dell'Ariete. Non ci possono essere dubbi al riguardo (vedi le Figure 2.25 e 2.26).

Figura 2.24.
Carta astrale da un libro del XVII secolo di Stanislaw Lubienietski. Si può vede che la stella Gamma dell'Ariete è stata scelta come punto di riferimento longitudinale iniziale. Qui è dove l'equinoziale attraversa l'eclittica. Tratta da [543], inserita tra le pagine 26 e 27.

Figura 2.25.
Frammento
. Lato destro della carta di Lubienietski, dove l'equinoziale
attraversa l'eclittica vicino alla stella Gamma dell'Ariete ([1257]).
Tratta da [543], inserita tra le pagine 26 e 27.

Figura 2.26.
Frammento. Lato sinistro della carta di Lubienietski,
dove l'equinoziale attraversa l'eclittica vicino alla stella Gamma dell'Ariete.
Tratta da [543], inserita tra le pagine 26 e 27.
Pertanto, tutte le longitudini stellari indicate da S. Lubienietski erano più piccole di circa 7 gradi di quelle che troviamo nella versione greca dell'Almagesto del 1538 (vedere anche le rispettive tabelle comparative come pure le carte vere e proprie in [544], Volume 4, pagine 233-234, e anche in [543], inserite tra le pagine 26 e 27).
Torniamo alla strana “logica” degli storici pro Scaligero, che sostengono con molta persistenza e persino ostinazione, la loro datazione dell'Almagesto tramite le longitudini dell'edizione greca, implicando così che Lubienietski calcolò le coordinate partendo dal punto dell'equinozio primaverile della sua epoca. In tal caso, il suo libro dovrebbe essere datato al V secolo a.C., poiché qui è quando “il punto dell'equinozio di primavera si trovava davvero vicino alle prime stelle della costellazione dell'Ariete, vedi il caso di Lubienietski”, secondo il commento adeguato di N. A. Morozov [544],Volume 4, pagina 33.Tuttavia, il libro di Lubienietski fu scritto nel XVI secolo!
Il conseguente corollario assurdo è un'altra prova di quanto bisogna essere cauti quando si ha a che fare con il “metodo di datazione” sopra descritto che, ci sentiamo obbligati a ribadirlo, è sempre stato utilizzato dagli storici pro Scaligero nel caso dell'edizione greca dell'Almagesto.
Tutto quanto sopra implica lucidamente che gli astronomi del XV-XVII secolo d.C. non erano ancora arrivati a un qualsiasi tipo di accordo unificato relativo al punto iniziale di riferimento per il calcolo della longitudine. L'epoca dell'unificazione arrivò dopo un po'. Ogni astronomo sceglieva il proprio punto di riferimento, guidato dalle proprie considerazioni. Lubienietski, per esempio, per questo scopo usò le prime stelle della costellazione dell'Ariete. Per quanto riguarda l'edizione greca dell'Almagesto, le coordinate stellari vennero contate dal meridiano che attraversava l'eclittica nel punto in cui la distanza longitudinale dalla stella γ dell'Ariete era uguale a 6°40'.
Il caso di Lubienietski non è affatto unico. Il catalogo stellare compilato da Copernico ci offre un esempio ancor più impressionante. Anche Copernico contò le longitudini iniziando con la γ dell'Ariete, proprio come Lubienietski (o piuttosto, quest'ultimo seguì la tradizione di Copernico). L'unica differenza è che nel catalogo di Copernico la γ dell'Ariete occupa la longitudine zero ([1076]). Quest'ultimo fornisce le sue coordinate pari a 0 gradi 0 minuti di longitudine e 7 gradi 20 minuti di latitudine (vedi [544], Volume 4, pagine 224 e 227). Quindi, se decidessimo di “datare” il catalogo di Copernico usando il “metodo di Scaligero” sopra descritto, lo faremmo risalire a un'epoca immemorabile, che sarebbe perfettamente sbagliato visto che si presume che Copernico sia vissuto nel XV-XVI secolo (1473-1543).
Pertanto, la precessione delle longitudini stellari dell'eclittica non può servire per la datazione sicura di un qualsivoglia catalogo.
I vari punti di riferimento iniziali, utilizzati per il calcolo della longitudine nelle opere degli autori del XVI-XVII secolo come indicato sopra, non dovrebbero sorprenderci affatto. C'erano molte diverse scuole astronomiche all'alba di questa disciplina, che spesso erano in competizione tra loro e avevano delle regole diverse per la compilazione di un catalogo. È possibile che ciascuna di quelle scuole rimase fedele alla propria tradizione, che specificava le leggi per la scelta dei punti base, dei punti di riferimento e così via. Le considerazioni per quel tipo di scelta devono essere state astronomiche, religiose o di natura completamente diversa.
Fu solo quando l'astronomia si sviluppò in una scienza ormai cresciuta, che ci si rese conto della necessità di un sistema unificato di indicazioni e concetti, e che il linguaggio astronomico doveva diventare più uniforme. In particolare, il punto dell'equinozio di primavera fu concordato come il punto di riferimento iniziale (invisibile, a dir il vero; inoltre, la sua posizione celeste cambia con il passare del tempo). Questo punto non può essere fissato a qualche stella situata nelle vicinanze. Pertanto non è certo sorprendente che alcuni astronomi medievali usavano una stella vera come riferimento, anziché il punto dell'equinozio: la stella γ dell'Ariete, per esempio.
Mentre studiamo il catalogo stellare dell'Almagesto nel nostro libro (lo stesso vale per gli altri vecchi cataloghi stellari), ci assicuriamo che la nostra ricerca non dipenda in alcun modo da presunzioni che riguardano il particolare punto di riferimento longitudinale utilizzato dal compilatore del catalogo. Dopo tutto, non ci sono quelle indicazioni nei veri cataloghi stellari. I nostri contestatori potrebbero controbattere dicendo che il riferimento diretto alla scelta del punto equinoziale per la misurazione delle longitudini, lo si può trovare ovunque nell'Almagesto.
Tuttavia, se volessimo essere guidati da quelle nozioni, ciò implicherebbe l'uso di alcune informazioni “estranee” o straniere che, come dobbiamo sottolineare, non sono contenute nel catalogo stellare. Tuttavia, il nostro obiettivo è quello di datare il catalogo con le sue caratteristiche interne senza citare alcuna fonte esterna. Per quanto riguarda la questione di determinare la datazione dei testi rimanenti insieme alla sua genesi, è un problema a sé stante, uno di quelli che non possiede un'unica soluzione affidabile (vedi [544] e [614]).
9. La dubbia natura dell'opinione tradizionale secondo la quale il testo di Tolomeo implica l’esecuzioni di vere “osservazioni”, così come la sua “partecipazione personale” alle misurazioni e alle osservazioni astrali descritte nell’Almagesto.
Il testo di Tolomeo non può in alcun modo sottintendere la veridicità dell'opinione consensuale, vale a dire che tutte le osservazioni e le misurazioni contenute nell'Almagesto furono eseguite dall'autore di persona. Il testo effettivo consente diverse interpretazioni. Tuttavia, è molto probabile che ciò che stiamo vedendo qui rappresenta il risultato del lavoro di moltissimi astronomi e non il resoconto di un singolo autore riguardo le sue osservazioni.
A parte questo, l'Almagesto fondamentalmente è un manuale o una guida per giovani astronomi e scienziati in generale, che contiene le descrizioni di vari metodi di osservazione, una sorta di enciclopedia astronomica medievale. Ecco alcuni esempi a conferma di questo. Useremo l'edizione dell'Almagesto di Toomer ([1358]).
Nella sua descrizione del cerchio di transito nel Capitolo 1, Tolomeo ci dice quanto segue: “Abbiamo realizzato un anello di bronzo della misura adatta [esattamente di che dimensioni? - autore] ...per usarlo come cerchio di transito, quindi l'abbiamo diviso in 360 parti [gradi]; ognuna di queste venne divisa in tante parti quante erano le dimensioni consentite dallo strumento [quante? - autore] ... Inoltre, abbiamo scoperto un metodo più semplice per condurre le misurazioni, forgiando una parete di pietra o di legno [?! - autore] da utilizzare al posto degli anelli” ([1358], pagine 61 e 62).
Ciò che vediamo qui ovviamente differisce dalla descrizione di un vero dispositivo utilizzato per le misurazioni da parte del solo Tolomeo, o da lui con la sua squadra. Come si potrebbero spiegare le espressione ambigue “della misura adatta”, “tante parti quante erano le dimensioni consentite dallo strumento”, o “una parete di pietra o di legno”? Veramente, era di pietra o di legno?
Tutto andrebbe a suo posto se ce la rimuovessimo l'opinione intrinseca scaligeriana e ci rendessimo conto che quello che abbiamo davanti non è il resoconto fatto da un osservatore, ma piuttosto un manuale enciclopedico che spiega a un potenziale studente o scienziato la costruzione di vari strumenti; diversi metodi di come condurre una ricerca, ecc...
Considerate il seguente passaggio dell'Almagesto, per esempio: “Prima di [del regno di] Antonino, quando abbiamo condotto la maggior parte delle osservazioni sulla posizione delle stelle immobili” ([1358], pagina 328). L'astronomia di Scaligero legge l'implicazione che in questa frase Tolomeo sta affermando la responsabilità personale per le osservazioni eseguite all'inizio del regno di Antonino Pio. La datazione di Scaligero di questo imperatore è il 138-161 d.C. Tuttavia, la frase di Tolomeo è piuttosto vaga e consente interpretazioni diverse. In primo luogo, chi siamo i “noi” che condussero le osservazioni? Tolomeo stesso o i suoi predecessori della stessa scuola scientifica? Inoltre, a cosa esattamente si sta riferendo con “la maggior parte delle osservazioni”? L'uso del “noi” deve essere considerato come un tratto distintivo dello stile letterario dell'autore dell'Almagesto, piuttosto che all'indicazione di una sua partecipazione effettiva alla ricerca; è anche possibile che furono gli autori della truffa del XVI-XVII secolo, con l'intenzione di creare un'impressione che il lavoro in questione fu scritto per descrivere la ricerca di una sola persona.
Ad esempio, prendiamo in considerazione le parole scelte da Tolomeo come introduzione al catalogo stellare dell'Almagesto. Sarebbe naturale aspettarsi che l'autore/osservatore che ha condotto lo studio si ponga delle domande per fornire delle descrizioni dettagliate su come sono state eseguite le sue ricerche, quali sono state le stelle che ha scelto come riferimento ecc... Niente del genere. Il testo di Tolomeo è molto vago:
“Di nuovo, lo stesso strumento [l'astrolabon- autore] permette di osservare tante stelle quante sono umanamente possibile, comprese quelle di sesta magnitudine. Abbiamo sempre diretto il primo anello alla stella luminosa più vicina, la cui posizione rispetto alla luna era già stata calcolata” ([1358], pagina 399).
Questo è seguito dalla descrizione del metodo utilizzato per i calcoli delle coordinate stellari quando la longitudine viene misurata per mezzo di stelle relativamente luminose e la latitudine è in relazione all'anello dell'eclittica dell'astrolabon. Questa descrizione viene fornita ancora una volta in modo piuttosto generale ed è seguita da una frase davvero notevole:
“Al fine di rappresentare le stelle in una solida cosmosfera secondo il metodo sopra descritto, abbiamo sistemato le stelle in una tavola a quattro colonne” ([1358], pagina 340). Più avanti troviamo le spiegazioni delle indicazioni utilizzate nella tavola. La “tavola” in questione è il famoso catalogo stellare. Perciò, abbiamo scoperto che il catalogo di Tolomeo è stato creato con lo scopo principale di usarlo per la creazione di una cosmosfera.
Lo diciamo nuovamente, assomiglia molto a un manuale. “Se si vuole creare un globo, bisogna fare questo e quello”. A proposito, Tolomeo fa un altro riferimento all'imperatore Antonino nella sua descrizione della “tavola”, ossia del catalogo: “Nella seconda colonna si trova il valore longitudinale che è stato dedotto dalla ricerca [condotta da uno scienziato anonimo - autore] all'inizio del regno di Antonino ([1358], pagina 340). Ancora una volta, non è necessario interpretare le parole di Tolomeo come la prova che condusse personalmente le osservazioni all'epoca di Antonino. Questa frase può essere anche interpretata nel modo seguente: un osservatore tardo medievale compilò il catalogo con i valori corrispondenti al regno di Antonino. A proposito, l'Almagesto non ci fornisce alcuna datazione per il regno di Antonino. Come già sappiamo, l'azione più semplice che può essere intrapresa al fine di compilare un catalogo con qualsiasi coordinata dell'eclittica nota a priori e appartenente a un'epoca antica, è la sottrazione di un appropriato valore costante dalle longitudini originali. Inoltre, questa nostra spiegazione viene esplicitamente confermata dal testo dell'Almagesto! Tolomeo continua il suo pensiero proprio lì: “I valori latitudinali rimangono sempre immutabili; per quanto riguarda i valori longitudinali [contenuti nel catalogo dell'Almagesto - autore], questi consentono di fare dei facili calcoli longitudinali anche per altri periodi temporali, per i quali la distanza tra l'epoca attuale e il periodo desiderato deve essere ricalcolata ipotizzando una velocità di alterazione pari a 1 grado ogni 100 anni. Il valore risultante dovrà quindi essere sottratto da quello dell'epoca attuale per poter ottenere una data nel passato, o aggiungerlo ad esso per una data nel futuro” ([1358], pagina 340).
Pertanto, Tolomeo offre una spiegazione perfettamente chiara di come si deve spostare il catalogo stellare nel tempo sottraendo la costante che lo avrebbe reso “più antico”, o aggiungendola per ottenere l'effetto opposto. Ancora una volta, è molto simile a un libro di testo in cui si spiega la tecnica per la datazione e la ridatazione dei cataloghi stellari agli studenti. Questo libro potrebbe anche essere stata una fonte utile per tutte le linee guida necessarie nel XVI-XVII secolo d.C., considerando soprattutto il fatto che la costruzione di una cosmosfera come descritta nell'Almagesto non ha bisogno di valori longitudinali assoluti, vale a dire che vengono contati da una stella immobile scelta arbitrariamente. Per questo scopo, Tolomeo suggerisce di usare Sirio ([1358], pagina 405).
A quanto pare, i valori assoluti delle latitudini eclittiche stellari, nell'astronomia di Scaligero non sono mai stati usati. Pertanto, il punto di riferimento longitudinale veniva scelto più o meno arbitrariamente. Copernico, per esempio, dopo aver copiato il catalogo dell'Almagesto nel Volume 6 del suo Revolutionibus Orbium Caelestium, in qualche circostanza conta le latitudini dalla stella γ della costellazione dell'Ariete, che si trovava alla distanza di 27° dal punto dell'equinozio di primavera all'epoca di Copernico.
Bisogna sottolineare che, come ci dice la storia dell'astronomia, pare che il lavoro di Copernico non venne “apprezzato” fino a un secolo dopo la sua morte, nell'epoca di Keplero, il XVII secolo ([614], pagina 328). Date un'occhiata al Capitolo 10 per maggiori dettagli. Possiamo quindi porci la domanda legittima riguardo la data esatta in cui è stato scritto o modificato il libro che ai nostri giorni viene attribuito a Copernico. Potrebbe essere stato all'inizio del XVII secolo e non nel XVI? In altre parole, nell'epoca di Keplero?
10. Quale punto dell’eclittica utilizzò Tolomeo come riferimento longitudinale?
Come già sappiamo, la scelta del punto di riferimento iniziale per il conteggio della longitudine influenza la datazione della precessione longitudinale del catalogo in misura sostanziale. Conduciamo uno studio più approfondito sulla questione di quale punto dell'eclittica fu usato da Tolomeo per i calcoli longitudinali nel suo catalogo. Si presume tradizionalmente che per questo scopo usò il punto dell'equinozio di primavera, come molti altri astronomi tardo medioevali.
Abbiamo scoperto che se per questo scopo volessimo usare solo il testo dell'Almagesto, la questione del punto di riferimento iniziale descritto da Tolomeo sarebbe tutt'altro che semplice ed impossibile da essere risolta senza controversie. Torniamo all'Almagesto per fornire le citazioni pertinenti.
Tolomeo scrive che “dovremo usare i nomi dei segni zodiacali per riferirci alle corrispondenti dodici parti del cerchio inclinato che dovranno iniziare nei punti degli equinozi e dei solstizi. La prima dodicesima parte che inizia nel punto dell'equinozio di primavera e la cui direzione è contraria a quella dell'Universo, sarà conosciuta come Ariete, la seguente come Toro ...” (II: 7- [704], pagina 45). I segni in questione sono semplicemente gli archi dello Zodiaco, non le longitudinali stellari. Inoltre, quando Tolomeo ci parla delle longitudini, descrive la seconda colonna (longitudinale) del suo catalogo stellare come segue: “Nella seconda colonna abbiamo trovato le loro [riferendosi alle stelle - autore] posizioni longitudinali edotte dalle osservazioni condotte all'inizio del regno di Antonino. Queste posizioni si trovano all'interno dei segni zodiacali; l'inizio di ogni quadrante zodiacale viene determinato da un solstizio o da un equinozio, vedi sopra” (VII: 4, [1358], pagina 340).
In effetti, le longitudini stellari dell'Almagesto sono indicate separatamente per ogni segno o arco dello zodiaco uniforme e sono state calcolate dall'inizio del rispettivo segno o arco. In altre parole, le longitudinali stellari che troviamo nell'Almagesto non possono essere considerate assolute e sono state conteggiate da un singolo punto scelto sull'eclittica. Al contrario, vengono date le relative longitudini contenute in ciascun rispettivo segno o arco dello Zodiaco uniforme, per un totale di 12. Viene anche sottolineato che uno dei quadranti è orientato nel punto dell'equinozio.
Pertanto, il calcolo di alcuni valori longitudinali assoluti richiede l'aggiunta di un certo numero intero di gradi divisibile per 30, ossia la dimensione di un certo segno o arco dello Zodiaco uniforme. Le longitudini eclittiche assolute del catalogo possono essere dedotte solo dopo questa procedura, che in linea di massima non è affatto complessa.
Descriveremo meglio con il seguente esempio. Nell'Almagesto, la longitudine della stella polare viene data come Gem 0°10'. Per calcolare il valore assoluto della longitudine, dobbiamo aggiungere un numero intero di gradi a 0°10' che sia pari a 60°, come suggerisce la tradizione contemporanea. Questo è il numero dei gradi che si ritiene corrispondano all'inizio del segno arco Gem dello Zodiaco uniforme. Dobbiamo quindi ottenere il valore di 60°10'. Se dovessimo considerarlo come la longitudine dell'eclittica della stella polare rispetto al punto dell'equinozio primaverile dovrebbe corrispondere alla posizione che quest'ultimo occupò all'inizio della nuova era.
Si osserva una situazione perfettamente simile con le longitudini rimanenti delle migliaia di stelle contenute nel catalogo dell'Almagesto. Nonostante la semplicità dei calcoli di cui sopra, occorre sottolineare che questa è la nostra prima opportunità di mal interpretare i dati sorgente offerti dall'Almagesto, vale a dire che il fatto che i valori dei gradi interi corrispondano ai segni zodiacali, dipende dalla scelta del primo segno o arco dello Zodiaco, il cui inizio coincide con il punto di riferimento iniziale: l'equinozio di primavera o qualche altro punto sull'eclittica. A quanto pare, l'alterazione del primo segno zodiacale altererà i gradi dei valori assoluti aggiunti. La vaghezza della frase di Tolomeo lascia molto spazio all'interpretazione.
Come scopriremo, la descrizione di Tolomeo della cosmosfera non usa il punto dell'equinozio primaverile come riferimento iniziale. Scrive che “siccome non ha senso contrassegnare i punti del solstizio e dell'equinozio sul globo dello Zodiaco (poiché le stelle non mantengono una distanza costante da questi punti), dovremmo scegliere un numero di punti di riferimento fissi e immutabili tra le stelle immobili. La più brillante di queste è la stella nella bocca di Canis Major [cioè Sirio! - autore] ...quindi, per ciascuna delle rimanenti stelle immobili del catalogo [a parte Sirio - autore] dobbiamo contrassegnare la sua posizione [longitudine - autore] ruotando l'anello graduato attorno al polo dell'eclittica; il punto che segneremo sull'eclittica di questo anello si troverà all'esatta stessa distanza dal punto di riferimento che abbiamo scoperto (Sirio), che nel catalogo si trova tra la stella in questione e Sirio” ([1358], pagina 405).
Per cui, Tolomeo ci fornisce un riferimento diretto a Sirio come l'inizio assoluto più conveniente per il calcolo della longitudine dell'eclittica. Tutto questo è completamente in contrasto con la versione consensuale che ci dice che Tolomeo utilizzò sicuramente il punto di equinozio di primavera come riferimento.
Inoltre, poiché l'Almagesto è un'enciclopedia astronomica, potrebbe essere che la sua forma attuale sia stata compilata attraverso le opere di vari astronomi provenienti da scuole diverse. Pertanto, per le varie parti dell'Almagesto potrebbero essere stati usati diversi principi di misurazione, in particolare è possibile che nel catalogo dell'Almagesto il punto di riferimento longitudinale vari a seconda della parte.
Tutto ciò indica che i tentativi di datare il catalogo di Tolomeo tramite la precessione longitudinale può portare ad errori gravissimi, che è esattamente ciò che vediamo in alcune opere moderne sulla storia dell'astronomia, vedi sotto.
Nascono anche altre questioni controverse. La citazione sopra menzionata dimostra che la creazione di una cosmosfera ha bisogno di circa 1000 operazioni astronomiche, vale a dire la sottrazione della longitudine di Sirio dalle longitudini delle altre mille stelle del catalogo. Tuttavia, la longitudine di Sirio viene espressa come una frazione nel catalogo dell'Almagesto, vale a dire 17°40' nei Gemelli. È perfettamente chiaro che l'operazione di sottrarre questo numero un migliaio di volte dalle altre longitudini, porterà via molto lavoro. D'altro canto, Tolomeo, che sosteneva l'uso di Sirio come riferimento, poteva benissimo scegliere un'altra stella molto luminosa: Arturo. E' una stella di grande magnitudine; ma soprattutto, la sua longitudine è espressa come numero intero nel catalogo, vale a dire 27° nella Vergine. Perché uno dovrebbe eseguire un migliaio di operazioni con delle frazioni, quando sarebbe molto più semplice e ci vorrebbe molto meno tempo fare le stesse operazioni con i gradi espressi tramite un numero intero?
Si può ovviamente presumere che un certo valore costante sia stato aggiunto o sottratto dalle lunghezze iniziali dell'Almagesto, trasformando la longitudine di Sirio in un valore frazionario anziché in un numero intero. Pertanto, questo valore doveva comprendere una certa quantità di gradi e 40 minuti, dal momento che la longitudine di Sirio nella versione moderna del catalogo dell'Almagesto equivale a 17°40'.
Qui è dove inaspettatamente ci imbattiamo in un'ottima concordanza con il risultato di R. Newton ([614]). Dimostra che le longitudini contenute nel catalogo sono state ricalcolate da qualcuno, con una quantità indefinita di gradi e 40 minuti aggiunti ai valori longitudinali originali e basa le sue conclusioni su delle considerazioni del tutto diverse e di natura statistica. Riteniamo che questa concorrenza tra le due diverse osservazioni è tutto tranne che casuale.
Bisogna fare la seguente osservazione generale che non ha alcuna relazione formale con l'astronomia, ma potrebbe rivelarsi ancora utile per la nostra comprensione del ruolo e del posto dell'Almagesto. La letteratura moderna sulla storia dell'astronomia ci dà l'impressione che i capitoli dell'Almagesto che hanno a che fare con le stelle siano una sorta di commentario o un allegato al documento centrale, che è il catalogo stellare. Tuttavia, noi siamo di un'opinione diversa. Il contenuto principale di questi capitoli sono le linee guida di Tolomeo per la costruzione della cosmosfera sulla quale si devono evidenziare le posizioni delle stelle. Il vero processo di costruzione, lo strumento che si deve usare per questo scopo, ecc... sono stati descritti con grande dettaglio; il catalogo in sé non è che una “tabella di riferimento” per la costruzione di una cosmosfera. È del tutto possibile che nel Medioevo quelle cosmosfere fossero utilizzate per scopi astrologici o mistici. Il fatto più curioso è che la storia dell'astronomia ha molti riferimenti per la costruzione delle cosmosfere; tuttavia, questa “epoca di costruzione del globo celeste” non è nemmeno vicina all'inizio della nuova era, ma appartiene al Medioevo. In particolare, le prime notizie di quei globi le abbiamo datate all'epoca di Tycho Brahe, il quale costruì lui stesso una cosmosfera ([395], pagina 127); veniva considerata un'attività importante. Ci viene detto che “la grande cosmosfera ottonata, 149 centimetri di diametro, merita di essere menzionata separatamente. Sulla sua superficie c'erano le rappresentazioni della cintura zodiacale, l'equinoziale e le posizioni delle 1000 stelle le cui coordinate furono determinate nel corso degli anni dalle osservazioni di Tycho. Tycho confessò con orgoglio: “Credo che nessun altro cosmo di queste dimensioni, costruito con tale accuratezza e precisione, sia mai stata fatto in tutto il mondo”. Affermò anche moltissima gente si recava in Danimarca appositamente per ammirare la cosmosfera. Ahimè, questa vera meraviglia dell’arte e della scienza scomparve durante un'esplosione nella seconda metà del XVIII secolo” ([395], pagina 127).
Per cui, i rispettivi capitoli dell'Almagesto si adattano perfettamente bene all'epoca del XVI-XVII secolo.
Inoltre, gli esperti in storia dell'astronomia suggeriscono che persino se le longitudini dell'Almagesto fossero state ricalcolate, sarebbero cadute in un'epoca più recente e mai indietro nel tempo. Siamo convinti che il ricalcolo delle vecchie longitudini stellari per l'epoca corrente fosse una pratica abbastanza comune tra gli astronomi del medioevo. Si fa anche riferimento ai primi cataloghi medioevali precedenti a Brahe. Si pensa che gli astronomi del Medioevo siano stati “troppo pigri” per condurre nuove ricerche. Preferivano prendere un “antico” catalogo risalente ai tempi immemorabili, alterare tutti i suoi valori con il fattore di una singola costante e inventare di conseguenza delle “moderne coordinate stellari”, per poi usare nelle loro ricerche il catalogo antico ma convenientemente “aggiornabile”.
Bisogna ammettere che questa ipotesi sembra piuttosto strana. È improbabile che tutte le nuove generazioni di astronomi si contendano la mera “fabbricazione” di un tipo di catalogo che per farlo dovevano spostare le longitudini contenute in alcuni cataloghi vecchi e piuttosto obsoleti. Ogni epoca nuova crea degli strumenti astronomici nuovi e più avanzati. Pertanto, è molto probabile che gli astronomi di ogni epoca successiva misurassero nuovamente le coordinate stellari con maggiore precisione. Non solo le longitudini diventavano più realistiche, ma anche le latitudini: le correzioni potevano variare da stella a stella. Di conseguenza, gli astronomi di ogni nuova generazione compilavano un nuovo catalogo estremamente accurato per loro stessi (come glielo consentivano i loro strumenti, ovviamente). Questo stesso metodo fu usato per scopi scientifici, come la navigazione, al contrario dei cataloghi obsoleti e quasi dimenticati che contenevano molti errori dovuti all'imprecisione dei primi strumenti antichi.
Se nel XVI-XVII secolo qualcuno cercava di fabbricare e introdurre una storia “antica” falsificata, allora l'approccio sarebbe stato radicalmente diverso. Si prendevano alcuni cataloghi stellari compilati di recente e si spostavano le longitudini nel “passato”, ossia “nell'epoca storica desiderata”, per esempio i primi anni del periodo dopo Cristo. L'operazione era semplice e non faceva perdere molto tempo ai truffatori. Dopodiché, rivendicavano a gran voce di aver scoperto “un catalogo stellare estremamente antico”. Ribadiamo che il metodo di falsificazione più semplice e veloce è quello di spostare le longitudini stellari usando un singolo valore costante. A quanto pare, è così che nacquero le “osservazioni personali” di Tolomeo nel II secolo d.C., così come le molte altre “osservazioni” condotte dai “primi astronomi medievali”. I truffatori non potevano semplicemente aprire un catalogo moderno, poiché sarebbero stati immediatamente colti in flagrante, per cui preferivano utilizzare un catalogo datato 100-200 anni indietro, già dimenticato e non più in stampa.
11. La sinusoide di Peter nelle latitudini dell’Almagesto.
Consideriamo ora le latitudini del catalogo stellare dell’Almagesto. Qui è dove scopriamo immediatamente un effetto molto particolare che sfida la spiegazione nel paradigma dei precedenti studi dell’Almagesto. Ci riferiremo a questo effetto con il termine “curva sinusoidale di Peters”. La questione è la seguente: Peters analizza la distribuzione media degli errori nell’Almagesto come una funzione longitudinale. A tale scopo calcola le posizioni delle stelle zodiacali nel cielo odierno per il 100 d.C., ossia la presunta epoca della creazione dell’Almagesto. Quindi, Peters calcola la discrepanza latitudinale di Δi = Bi- bi. Pertanto, secondo Peters Bi è il valore latitudinale della stella i presa dall’Almagesto, mentre e bi è il significato della sua latitudine per il 100 d.C. Pertanto, il valore Δi dimostra “l’errore di Tolomeo” nella determinazione della latitudine i della stella, fatta supponendo che l’Almagesto fu creato intorno al 100 d.C. Peters procede con la divisione dell’eclittica in intervalli di 10 gradi e quindi calcola il valore medio della discrepanza latitudinale per tutte le stelle dell’Almagesto che finiscono in questo intervallo, valore che naturalmente varia da un intervallo all’altro.
Di conseguenza, è stato creato un grafico speciale che dimostra in che modo la discrepanza media latitudinale si manifesta lungo l'eclittica. I punti dell'eclittica possono essere caratterizzati dalla longitudine; come conseguenza, il grafico costruito rappresenterà la discrepanza latitudinale come una funzione longitudinale. La curva sinusoidale di Peters può essere vista nella Figura 2.27. È molto simile a una curva sinusoidale con un'ampiezza di circa 20'. Si potrebbe scegliere una curva sinusoidale che viene considerata la migliore nella sua classe perché si avvicina alla curva della Figura 2.27. Questa curva prende il nome da Peters.
L'aspetto della sinusoide di Peters è molto difficile spiegare all'interno della struttura che racchiude le idee moderne dell'Almagesto. Ad ogni modo, non abbiamo trovato una ragionevole spiegazione di questo fenomeno distintamente periodico in qualsiasi genere di letteratura.
Bisogna sottolineare che [1339] non contiene dettagli correlati al calcolo di questa curva da parte di Peters. Nello specifico, non sappiamo nulla su quali stelle dello Zodiaco usasse per i calcoli. Pertanto, al fine di confermare l'esistenza reale dell'effetto e studiarla, abbiamo dovuto ricalcolare la curva in questione per tutte le stelle zodiacali con l'aiuto di un computer. I nostri risultati, nonché le loro implicazioni e i relativi commenti, li potete trovare nei capitoli che seguono. Tuttavia, saltiamo per un momento tutta la questione e diciamo ai lettori che abbiamo trovato una spiegazione perfetta per questa strana sinusoidale.
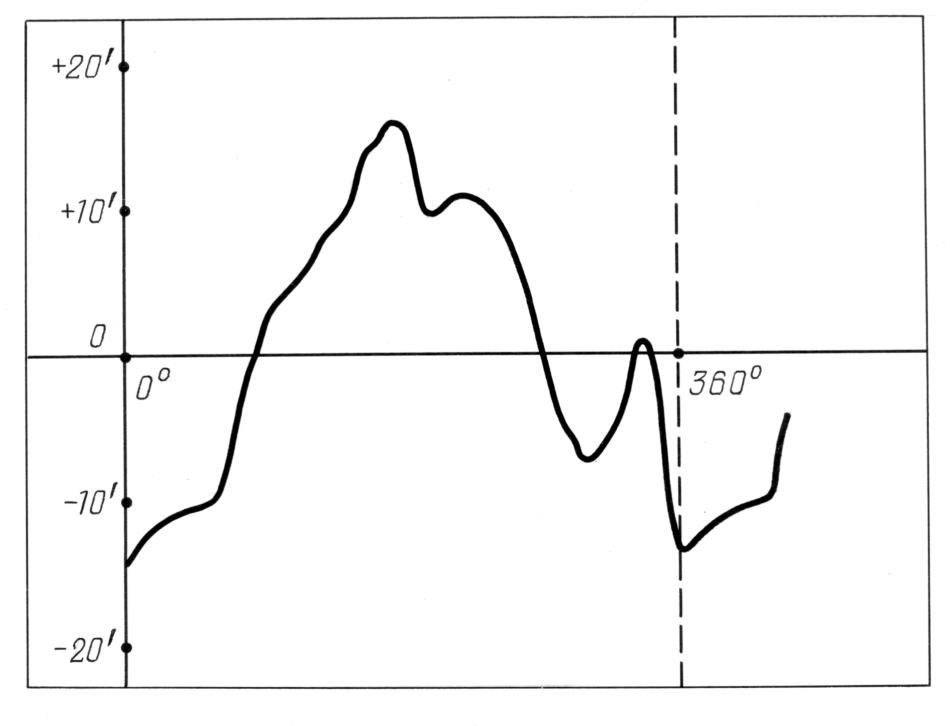
Figura 2.28.
Il grafico un po' strano della discrepanza longitudinale media come
funzione della longitudine eclittica nel catalogo dell'Almagesto.
N.B. A parte le latitudini, Peters studiò anche le longitudini del catalogo dell'Almagesto ([1339]). Calcolò la discrepanza latitudinale media per i settori di 10 gradi e ne ricavò ne il grafico che vediamo nella Figura 2.28. La curva rappresenta il comportamento della discrepanza longitudinale media come una funzione della longitudine dell'eclittica. È notevole che il grafico sia drasticamente diverso da quello con le latitudini dell'Almagesto. Il grafico longitudinale non è affatto sinusoidale; la sua amplitudine è più piccola; oltretutto ha due massimi locali piuttosto distinti. È possibile che questa natura stranamente irregolare della curva “longitudinale” sia il risultato del misterioso ricalcolo della longitudine dell'eclittica scoperto da R. Newton in [614] (vedere sezione 8). Come è stato fatto notare, le longitudini del catalogo dell'Almagesto non sono affatto una fonte affidabile di informazioni; pertanto, non abbiamo nessun motivo per studiare il grafico risultante in modo più attento. Tale analisi avrebbe senso solo se i meccanismi di ricalcolo delle longitudini, che devono essere stati usati dagli astronomi successivi (forse del XVI-XVII secolo), potrebbero essere ricostruiti, cosa che a questo punto riteniamo che sia molto difficile.