CAPITOLO 3
I tentativi senza successo di datare l’Almagesto. I motivi dei fallimenti.
Il nostro nuovo approccio e un breve resoconto dei nostri risultati.
4. L’analisi dei numerosi sforzi sbagliati riguardo la datazione dell’Almagesto attraverso i moti propri delle stelle
4.1. Molti errori non sono stati prodotti da fenomeni astronomici, ma derivano dall’errata applicazione dei metodi forniti dalla matematica statistica.
Analizziamo i tentativi di alcuni autori di datare l'Almagesto con i moti propri delle stelle.
Gli articoli degli astronomi Y. N. Yefremov e Y. D. Pavlovskaya ([273] e [274]) sono stati scritti in riferimento alle nostre pubblicazioni; rappresentano il tentativo di confermare la datazione scaligeriana del catalogo stellare dell'Almagesto tramite il moto proprio delle stelle. Il corollario formulato in [273] è il seguente. Il catalogo dell'Almagesto può essere datato agli inizi dell'era dopo Cristo per mezzo del moto proprio delle stelle e con una soglia di precisione di ± 100 anni. Gli autori arrivano fino a nominare la data del 13 d.C. ± 100 anni.
In [274], che è una pubblicazione più approfondita, gli autori formulano il loro corollario con maggiore cautela: “Il catalogo stellare dell'Almagesto è già stato osservato nell'antichità; molto probabilmente da Ipparco. È comunque possibile che le stelle più luminose furono osservate dallo stesso Tolomeo. Una sorta di argomentazione a supporto di questo la si può trovare nel fatto che le epoche che abbiamo ottenuto per Arturo e Sirio, le due stelle di prima magnitudine presenti nel nostro campione, sono di 2-4 secoli più recenti delle restanti stelle” ([274], pagine 189-190).
Tuttavia, i contenuti effettivi di [273] e [274] non implicano un tale corollario. Seguiamo brevemente i modelli di ragionamento di Y. N. Yefremov e Y. D. Pavlovskaya usando la loro pubblicazione più estesa ([274]), sebbene tutto ciò che diremo farà riferimento anche al loro precedente lavoro ([273]). Vi facciamo notare che Y. N. Yefremov non ha mai pubblicato testi scientifici su questo argomento prima delle menzionate opere ([273] e [274]) nel 1987 e nel 1989. Tuttavia, alcuni dei suoi articoli più popolari sono apparsi nei giornali e nelle riviste letterarie. Occorre inoltre dire che entrambe le sue pubblicazioni ([273] e [274]) contengono degli errori che abbiamo segnalato all'autore nel nostro libro [Metodi 3]: 2, pagine 99-103. Sarebbe opportuno che il signor Yefremov corregga questi errori prima che i risultati della sua ricerca vengano pubblicati sulla stampa popolare. Inoltre, riteniamo che questi errori non possano essere corretti, in particolare a causa delle datazioni sbagliate fornite da Y. N. Yefremov, vedi di seguito.
La datazione dei cataloghi stellari con il metodo descritto in [273] e [274] si basa sul confronto delle configurazioni stellari che cambiano nel corso di tempo, con le rispettive configurazioni indicate nell'Almagesto. Abbiamo scoperto che il ruolo principale nel cambio della configurazione viene svolto da una sola stella contenuta al suo interno, la più veloce (“il gruppo di Arturo”, “il gruppo di τ Cet”, ecc...). Useremo la stessa terminologia.
La datazione di un catalogo per mezzo di una singola configurazione dovrebbe essere quella per cui l'insieme delle distanze a due a due tra le stelle della configurazione che cambia, è il più vicino all'insieme delle distanze indicate nell'Almagesto. La prossimità viene definita con il senso quadratico medio.
Ovviamente, come conseguenza ciò che si ottiene è una certa approssimazione della data in cui Tolomeo o chiunque sia stato il compilatore del catalogo dell'Almagesto stavano facendo delle osservazioni, non la data effettiva. Uno si potrebbe chiedere: quali sono i possibili tassi di discrepanza di tale approssimazione? Non c'è una risposta concreta a questa domanda in [274].
La discussione sulla questione dei tassi di discrepanza per le datazioni risultanti viene esclusa a favore del riferimento al grafico delle dipendenze della discrepanza media quadratica tra le serie di distanze a due a due nell'Almagesto come pure sulla vera sfera celeste e la presunta datazione delle osservazioni condotte dall'autore del catalogo dell'Almagesto. Ci viene detto che “l'epoca T0 può essere stimata con sufficiente fiducia, il minimo della funzione ![]() (t) è drastico e profondo” ([274], pagina 183). Tuttavia, l'illustrazione a cui si riferiscono gli autori di [274] (pagina 185, ill. 3) implica che l'alterazione della presunta datazione di 1000 anni altera il valore della discrepanza media quadratica
(t) è drastico e profondo” ([274], pagina 183). Tuttavia, l'illustrazione a cui si riferiscono gli autori di [274] (pagina 185, ill. 3) implica che l'alterazione della presunta datazione di 1000 anni altera il valore della discrepanza media quadratica ![]() di un mero 13' al massimo per tutte le configurazioni, tranne un solo gruppo, quello di o2 Eri. Di seguito parleremo ulteriormente di questo gruppo.
di un mero 13' al massimo per tutte le configurazioni, tranne un solo gruppo, quello di o2 Eri. Di seguito parleremo ulteriormente di questo gruppo.
Vediamo quanto è davvero significativa la deviazione di 13' dalla discrepanza quadratica media per la situazione considerata da Y. N. Yefremov e Y. D. Pavlovskaya. Il valore del grado di scala dell'Almagesto è pari a 10', mentre la soglia effettiva di precisione delle stelle nell'Almagesto, stimata come discrepanza quadratica media dell'arco, è uguale a circa 30' (vedere [1339] e [614]). Se volessimo basare le nostre stime sui moti propri delle stelle studiate, ciò implicherebbe che la stima della precisione secondo il metodo offerto in [274], che si basa sulla minima discrepanza di configurazione quadratica media, debba consentire al valore di questa discrepanza di fluttuare all'interno di un intervallo maggiore di 13', circa 20'-30'. Questo porta a intervalli di datazione di 2-3 millenni. In altre parole, il possibile tasso di discrepanza per le date citate in [274] è uguale a 1000-1500 anni. Di seguito potete vedere ulteriori dettagli riguardanti la precisione del metodo correlato in [273] e [274]. Tuttavia, datando le osservazioni eseguite dal compilatore dell'Almagesto con una precisione così bassa, non ci consente di distinguere l'epoca di Tolomeo dalla nostra, figuriamoci le datazioni di Scaligero delle rispettive vite di Ipparco (II secolo a.C.) e Tolomeo (II secolo d.C.). Questo risultato ha un valore scientifico pari a zero. In ogni caso, è ovvio che l'Almagesto fu creato negli ultimi due millenni.
Pertanto, questo errore, così come gli errori realizzati dagli autori in questione che ne conseguono, è di natura matematica e non astronomica. I metodi della matematica statistica sono stati usati male, se non del tutto ignorati. Le affermazioni fatte da Y. N. Yefremov in riferimento alla presunta “alta precisione” dei suoi metodi non resistono alle critiche più semplici. È molto singolare che, dopo tutti questi anni, Y. N. Yefremov continui a insistere pubblicamente sulla veridicità dei suoi risultati errati nel campo della datazione dell'Almagesto: la situazione rimane come descritta sopra. Stiamo parlando dei suoi numerosi discorsi pubblici e delle pubblicazioni su riviste e giornali popolari orientati al grande pubblico.
4.2. Nelle opere di Y. N. Yefremov, i dati riguardanti la datazione dell’Almagesto sono stati ritoccati in modo che si adattassero al risultato desiderato.
Y. N. Yefremov e Y. D. Pavlovskaya in [274] affermano che il metodo di datazione del catalogo stellare da loro offerto è stato testato su tre cataloghi datati in modo veritiero, vale a dire i cataloghi di Ulugbek, Tycho Brahe ed Hevelius, e che l'applicazione del metodo in questione a tutti e tre i cataloghi ha dato un risultato incredibilmente preciso. Le date in cui furono compilati i cataloghi di Tycho Brahe sono state “ritoccate” con una soglia di precisione di 30-40 anni, mentre il catalogo di Ulugbek, il meno preciso dei tre, fu datato con una precisione sbalorditiva di ± 3 anni!
Tuttavia, non si può trascurare la circostanza allarmante che ciascuna di queste datazioni sia stata calcolata per mezzo della sua configurazione stellare, vale a dire che le datazioni dei cataloghi di Tycho Brahe ed Hevelius sono state ottenute dai gruppi di Arturo, mentre la datazione del catalogo di Ulugbek deriva dai dati ottenuti dal gruppo di τ Cet. Le altre configurazioni stellari per ciascuno dei tre cataloghi in questione non sono state affatto prese in considerazione. Perché mai? Risponderemo prontamente a questa domanda.
Inoltre, il risultato principale di Y. N. Yefremov e Y. D. Pavlovskaya in merito alla datazione dell'Almagesto è stato di fatto ottenuto da una sola e solitaria configurazione: il gruppo o2 Eri, sebbene abbiano formalmente affermato di aver studiato 13 configurazioni. L'analisi delle datazioni che è scaturita per tutti e tre i cataloghi, dimostra che in ciascun caso la scelta della vera configurazione stellare utilizzata per la datazione del catalogo è stata condizionata dalla datazione scaligeriana di detto catalogo, di cui gli autori di [273] e [274] stavano cercando di provarne la veridicità. In altre parole, in [274] Y. N. Yefremov e Y. D. Pavlovskaya scelsero per ciascun catalogo quelle configurazioni stellari che meglio concordavano con la datazione di Scaligero della compilazione del catalogo. Questo “metodo” è un semplice adattamento dei risultati della ricerca in modo tale che corrispondano ai valori desiderati noti a priori.
Tutto ciò rende totalmente privi di sostanza i risultati rivendicati in [273] e [274]. Questi risultati sono errati e quindi non possono confermare le datazioni di Scaligero dei vecchi cataloghi stellari.
4.3. Il circolo vizioso nelle datazioni dell’Almagesto per mezzo del moto della stella o2 Eri.
Analizziamo più nei dettagli la datazione dell'Almagesto per mezzo del gruppo di o2 Eri, come viene offerta nelle opere di Y. N. Yefremov ([273] e [274]), poiché è su questa datazione che Y. N. Yefremov basa di fatto le sue conclusioni.
Abbiamo già parlato della stella o2 Eri in precedenza, nel paragrafo 1. Tenete presente che la sua identificazione come una delle stelle dell'Almagesto dipende in gran parte dalla presunta datazione del catalogo. In altre parole, la risposta alla domanda su “chi sia chi nell'Almagesto”, o in altre parole, se la stella o2 della costellazione di Eridano sia stata o meno rappresentata nell'Almagesto e se così fosse con quale nome, varia in misura eccezionale come cambia la datazione nota a priori del catalogo.
Ricordiamo ai lettori che la stella o2 Eri si muove abbastanza velocemente, per cui la sua posizione celeste cambia. Nel corso del suo moto viene identificata consecutivamente con diverse stelle dell'Almagesto, vale a dire le tre che si trovano nell'intervallo storico degli ultimi 2.500 anni. La numerazione di Bailey di queste stelle dell'Almagesto è la seguente: 778, 779 e 780. La stella 779 viene tradizionalmente identificata con o2 Eri (vedi [1339]) per il semplice fatto che all'inizio della nuova era la stella o2 Eri occupava una posizione vicina a quella della stella 779 sull'atlante stellare dell'Almagesto.
Tuttavia, ciò che abbiamo davanti è chiaramente un'implicazione del fatto che l'Almagesto sia stato datato approssimativamente all'inizio della nuova era. Se non dovessimo fare delle supposizioni in riferimento alla datazione dell'Almagesto, troveremmo immediatamente altri candidati che potremmo identificare con la stella in movimento o2 Eri. Ad esempio, nell'intervallo del 900-1900 d.C., la stella che corrisponde alla posizione reale di o2 Eri è la 780. D'altro canto, la stella 779 dell'Almagesto non rimane senza identità neanche in questo caso, poiché può essere correttamente identificata con la stella 98 Heis (vedi [1339],pagina 117). Inoltre, questa stella venne identificata proprio così anche dall'astronomo Pierce, vedi [1339].
Dobbiamo sottolineare che la stella o2 della costellazione di Eridano è piuttosto fioca, come quelle che la circondano. Le loro magnitudini vanno da 4,2 a 6.3. Pertanto, l'unico modo per identificarle come stelle dell'Almagesto è il confronto delle coordinate. La luminosità di queste stelle è all'incirca la stessa e le descrizioni verbali di Tolomeo sulle stelle in questa parte di Eridano sono laconiche ed estremamente vaghe. Pertanto, è impossibile avere un'identificazione affidabile di queste stelle con qualsiasi altra caratteristica all'infuori delle coordinate. La “prova” che o2 Eri sia stata identificata in modo veritiero come una stella del catalogo dell'Almagesto, come citato in [274], si basa sulle ultime identificazioni delle stelle dell'Almagesto o, in alternativa, sulla datazione del catalogo al II secolo d.C. L'uso di tale “prova” per le datazioni indipendenti, ovviamente ci conduce a un circolo vizioso.
Pertanto, ciò che vediamo nelle opere di Y. N. Yefremov e dei suoi coautori ([273] e [274]) è che l'assunto che l'Almagesto sia stato compilato agli inizi della nuova era, è stato utilizzato come base per il corollario che l'Almagesto risale al 13 d.C. ± 100 anni. Questo è il circolo vizioso di cui stiamo parlando.
4.4. Gli errori di Y. N. Yefremov nella stima di precisione della datazione dell’Almagesto per mezzo di Arturo.
Passiamo ora ad Arturo, la seconda e l'ultima stella discussa nel lavoro di Y. N. Yefremov e Y. D. Pavlovskaya ([273]). L'identificazione di Arturo nell'Almagesto è inequivocabile. La prima datazione dell'Almagesto tramite il moto proprio in cui ci imbattiamo [273] è il 250 d.C. Dopodiché gli autori hanno “adattato” questa datazione e sono giunti al 310 d.C. ± 360 anni, data calcolata da una delle configurazioni. Parleremo di questo “adattamento” più avanti.
L'incertezza dei risultati pubblicati in [273] e[274] è stata anche commentata da altri autori. M. Y. Shevchenko, per esempio, in riferimento a [273] osserva giustificatamente che “il catalogo risale al I secolo avanti Cristo; tuttavia, la precisione e quindi la veridicità di questo risultato ancora oggi lascia molto a desiderare”, pagina 184 di [968].
Alcune semplici considerazioni consentono una stima facile della vera precisione su cui è basato il principio guida del metodo (come riferito in [273]). Infatti, la posizione nell'Almagesto di una data stella in movimento viene determinata in relazione ad alcune stelle nelle sue vicinanze ([273]): nel caso di Arturo con il “gruppo di Arturo”. Il gruppo di Arturo contiene 11 stelle. La posizione di Arturo in relazione a questo gruppo viene utilizzata per la stima della sua posizione sulla carta stellare calcolata teoricamente a ritroso per l'epoca t. Queste posizioni vengono poi confrontate tra loro.
Tutte le stelle dell'Almagesto sono state misurate con un qualche tipo di errore. Questo vale sicuramente per i “gruppi” di stelle, in particolare per tutte le stelle del gruppo di Arturo. Tuttavia, ipotizziamo temporaneamente che le misurazioni delle stelle nelle vicinanze di Arturo furono eseguite con una precisione ideale. Anche in questo caso, il tasso di errore riguardo la posizione di Arturo nell'Almagesto non può essere inferiore a 10' da qualsiasi coordinata, poiché questo è il grado di valore della scala delle coordinate nel catalogo stellare dell'Almagesto. In realtà, questo tasso deve essere aumentato a causa delle coordinate imprecise delle stelle in un determinato gruppo.
Questo porta a un errore nella distanza dell'arco di circa 14', secondo [273]. Se il possibile tasso di errore per ciascuna delle coordinate fosse uguale a 10', secondo il teorema di Pitagora l'ipotenusa dovrebbe essere pari a 14'. La velocità del moto proprio di Arturo è di circa 2" all'anno. Pertanto, Arturo copre una distanza di 14' in circa 420 anni. Questa è solo una stima approssimativa riguardo la precisione del “metodo”.
In realtà, la precisione effettiva della posizione di Arturo nell'Almagesto potrebbe avere un tasso di errore che supera sostanzialmente i 14' e le stelle fioche nelle sue vicinanze potrebbero essere misurate con ancor meno precisione. Ciò a cui ci stiamo riferendo ora è naturalmente l'errore nella distanza dell'arco. Come vedremo di seguito, la latitudine di Arturo è stata misurata con sufficiente precisione nell'Almagesto. Tuttavia, non è così per la sua longitudine (vedi la ricerca di Robert Newton in [614], per esempio). Inoltre, non ci sono ragioni per supporre che Tolomeo misurò con precisione un qualsiasi gruppo di stelle fioche. Pertanto, la vera precisione del “metodo” descritto in [273] è molto peggio di 420 anni. Per cui, l'intervallo delle possibili datazioni dell'Almagesto ottenuto con questo metodo è noto a priori per essere maggiore del 200 a.C. - 700 d.C.
Commentiamo ora l'errore casuale nel metodo di modellamento offerto in [273] e [274] per stimare la precisione della risultante datazione. Per esempio, questo “metodo” portò Y. N. Yefremov alla conclusione che la sua datazione dell'Almagesto al 300 d.C. circa, avesse una precisione di ± 300-400 anni (vedere [273], pagina 311 e [274], pagina 181).
Ai fini della datazione, in [273] e in [274] è stato usato il metodo dei minimi quadrati. I calcoli elementari citati sopra dimostrano che la precisione di questo metodo deve essere stimata secondo il tasso del singolo errore pertinente alla posizione della stella in questione nell'Almagesto, diviso per la velocità del suo moto proprio.
Y. N. Yefremov utilizza il metodo di modulazione casuale degli errori dell'Almagesto per aumentare la precisione del suo metodo. La precisione del metodo di modellamento che lui suggerisce (le molteplici perturbazioni delle coordinate stellari dell'Almagesto risultanti dal'applicazione di un valore casuale “comparabile” alla precisione del catalogo) non è stata stimata da nessuna parte nelle sue opere. Tuttavia, questo metodo funzionerà solo se i risultati di queste perturbazioni casuali faranno avvicinare le coordinate stellari dell'Almagesto a quelli reali con una probabilità “distintiva”. Tuttavia, a causa dell'effetto del singolo errore menzionato sopra, la probabilità di tale coincidenza con l'area delle coordinate effettive sarà molto bassa. Ad ogni modo, questa probabilità deve essere stimata; in [274] non c'è un solo accenno a tale stima. In linea generale, dal punto di vista della matematica statistica i metodi offerti dagli autori di [273] e [274] fanno acqua da tutte le parti.
Il “metodo di modellamento della datazione” offerto da Y. N. Yefremov può essere formulato nel seguente modo. Prima si deve considerare la certa vicinanza di una stella veloce, Arturo per esempio. Quindi, si deve usare il metodo dei minimi quadrati per determinare la data che ci dà la minima discrepanza media quadratica della distanza reciproca delle stelle dell'Almagesto dall'insieme degli stessi valori nella configurazione stellare effettiva che si altera nel tempo. Questa datazione è usata per stimare la data reale in cui fu compilato il catalogo, che è sconosciuta. Yefremov identifica questa datazione con T0.
Inoltre, il minimo risultante dalla discrepanza media quadratica, per qualche motivo viene dichiarato essere la stima della dispersione dell'errore locale nel catalogo dell'Almagesto. Yefremov ci dice piuttosto chiaramente che “raggruppando la stessa quantità n di stelle in modi diversi, otterremo il numero di stime ελ,β che non sono indipendenti. Pertanto, al posto di calcolare la media sceglieremo il valore massimo che sarà considerato come la stima dell'errore locale per la determinazione delle coordinate nel catalogo dell'Almagesto” ([273], pagina 311). E' lecito chiedersi il perché. In primo luogo, l'errore locale dell'Almagesto deve essere stimato separatamente, che è necessario per comprendere qual è il livello minimo di variazione che possiamo tollerare al fine di ottenere in modo affidabile la datazione reale della compilazione del catalogo. Quando Y. N. Yefremov prende il valore minimo effettivo per la stima della dispersione, è praticamente incapace di consentire la minima variazione.
In secondo luogo, il volume del campione utilizzato per la media del valore in questione è troppo piccolo (circa 5-6 osservazioni indipendenti) e non consente di prendere in considerazione la stima di Y. N. Yefremov come abbastanza precisa. L'errore locale deve essere stimato con una quantità maggiore di stelle.
Inoltre, Y. N. Yefremov modella le perturbazioni casuali delle coordinate di Tolomeo usando come base il tasso “stimato” di errore locale. Scrive che “la conoscenza del tasso di errore ελ,β per ciascun gruppo rende possibile condurre un esperimento numerico per poter studiare in che modo la stima di T0 venga influenzata dagli errori casuali nelle coordinate. Modelliamo le correzioni delle coordinate stellari dal catalogo dell'Almagesto, considerando che queste correzioni devono essere distribuite normalmente con una media di zero e l'errore quadratico medio ελ,β per ciascun gruppo, quindi calcolare il rispettivo valore di T0. Dopo aver ripetuto la procedura 100 volte, possiamo costruire un grafico di distribuzione per le stime risultanti di T0” ([273], pagina 312). Yefremov continua a dirci che “l'intervallo comune per tutti i gruppi con gli errori quadratici medi per le epoche prese in considerazione, è il I secolo a.C.” ([273], pagina 313). Yefremov fa anche la seguente affermazione sbalorditiva: “il tasso di probabilità che il valore casuale di T0 superi 900 è pari a 0,2 e riguardo a un gruppo ha la massima dispersione. Pertanto, è improbabile che il catalogo dell'Almagesto sia una contraffazione medievale” ([274], pagine 188-189). Per cui, a quanto pare Yefremov presume che la data media debba essere abbastanza vicina alla sua “data modellata casualmente”, stimando questa vicinanza “tenendo conto degli errori medi quadratici calcolati in precedenza” ([273], pagina 313).
Questo approccio è totalmente delirante. È ovvio che ciò che Yefremov dice essere la data media modellata T0, è semplicemente la sua stima iniziale di T0 con l'aggiunta casuale di qualche perturbazione. Per quanto riguarda la distribuzione delle date modellate, quella che viene fuori è una dispersione casuale con il centro pari a T0 per un dato gruppo. Yefremov è dell'opinione che la data effettiva deve essere vicina al centro di questa dispersione, in altre parole che le perturbazioni casuali da lui introdotte hanno una certa reale probabilità di coprire le vere posizioni delle stelle di Tolomeo. In altre parole, spera che il suo modellamento annulli casualmente gli errori di Tolomeo, stimando come vera la loro probabilità. Questo è il significato esatto del passaggio citato sopra, dove Yefremov ci dice che una datazione post 900 d.C. può essere raggiunta solo nel corso di questo modellamento con “il tasso di probabilità minimo dello 0,2”. E' dell'opinione che ciò renda altamente improbabile la datazione medievale dell'Almagesto.
Tuttavia, bisogna tenere presente che la sua iniziale datazione T0, che raggruppa le datazioni modellate, differisce dalla data effettiva per un certo valore. Come abbiamo dimostrato in precedenza con dei semplici calcoli, il valore di questo spostamento può essere abbastanza grande. Nel caso di Arturo, il suo valore più basso possibile è 420 anni, vedi sopra. Tale spostamento viene definito dall'errore singolo di Tolomeo nella stima delle coordinate di una determinata stella, così come dagli errori singoli per le stelle del gruppo scelto. Inoltre, i nostri calcoli dimostrano che il valore in questione dipende ampiamente dalla scelta del gruppo. Pertanto, alcuni errori singoli sono già inerenti al valore T0, probabilmente quelli gravi. Quando Yefremov “modella” i suoi errori aggiuntivi per i gruppi di stelle, li distribuisce già attorno a una certa datazione che potrebbe essere spostata lateralmente in misura sostanziale. Tuttavia, nel suo riferimento ai grafici delle distribuzioni modellate, Y. N. Yefremov sembra presumere che la datazione effettiva debba essere situata in ogni caso vicino al centro di queste distribuzioni, almeno entro un certo intervallo di confidenza con il rapporto di probabilità di 0,8, poiché considera troppo bassa la probabilità di 0,2.
Questo non è vero. La stima semplice sopra citata dimostra che la data effettiva è abbastanza lontana dal centro della distribuzione modellata (per esempio, questo intervallo supera i 420 anni per Arturo, vedi sopra). Allo stesso tempo, l'intervallo di dispersione delle date modellate attorno a una data spostata, potrebbero non essere affatto grande. Il fatto è che Yefremov ha preso il valore irragionevolmente basso dell'errore medio quadratico ottenuto dal valore minimo della parabola per questo modello, e per qualche ragione non ha effettuato delle stime specifiche di questo errore.
A parte questo, è abbastanza facile stimare che persino se si volesse modellare la correzione delle coordinate di una singola stella, la probabilità di tornare alla sua vera posizione sarebbe in linea di massima molto piccola. Questo viene confermato dal seguente semplice calcolo. Supponiamo che l'errore singolo di Tolomeo per una determinata stella sia pari a 45 gradi d'arco. Questi errori sono tipici nell'Almagesto: un buon numero di stelle che contiene sono state misurate molto male ([1339]). Ribadiamo che ci stiamo riferendo all'errore dell'arco. Come dimostreremo di seguito, gli errori della latitudine sono molto più piccoli.
Se applicassimo i calcoli sopra riportati ad Arturo, per esempio, l'implicazione sarebbe che per modellare una datazione effettiva che differirebbe dall'originale di 400 anni al massimo, bisognerebbe “centrare” l'intervallo di 14 minuti attorno alla posizione effettiva della stella (a condizione che le stelle del gruppo siano già cadute nelle posizioni necessarie e non influenzino troppo la datazione). La massima probabilità che il valore rientri in questo spazio di 14 minuti da una posizione spostata di 45', può essere stimata come la probabilità che cada nel settore ombreggiato della Figura 3.13a.
Se dovessimo considerare la probabilità che un punto perturbato situato nel raggio di 60' dal punto A sia pari a 1, finiremmo per avere una probabilità di 0,1 che la sua posizione si trovi nel settore ombreggiato. Per cui, anche in questo caso ideale il tasso di probabilità di ottenere casualmente la datazione necessaria, non la data corretta, ma piuttosto una che non differisca da essa di oltre 400 anni, sarebbe pari a 0,1. Tuttavia, Y. N. Yefremov è dell'opinione che la soglia di probabilità di 0,2 sia già sufficiente per rifiutare come improbabile una datazione post 900 d.C.
Gli autori di [274] affermano che i risultati dei calcoli eseguiti per le altre stelle veloci (che per qualche motivo non sono stati citati nel loro lavoro) confermano le conclusioni fatte nello studio di Arturo e o2 Eridano. Tuttavia, questa affermazione non corrisponde alla realtà.
Forniamo un solo esempio ma evidente. Tra le stelle veloci che sono state analizzate dagli autori di [273] e [274] troviamo Procione, una stella molto famosa nell'astronomia medievale. La nostra ricerca (vedi il paragrafo 1, per esempio) dimostra che il metodo di Yefremov deve aver portato alla datazione del X secolo d.C. circa grazie a Procione, che contraddirebbe palesemente le sue conclusioni. Per qualche motivo misterioso, in [273] non si dice assolutamente nulla dei risultati per la stella Procione.
Infine, il “metodo” descritto in [273] e [274] è ampiamente dipendente dalla scelta del contingente del gruppo per la stella veloce oggetto di studio. Abbiamo verificato in che modo il risultato della datazione da parte del gruppo Arturo, varia a seconda della scelta delle diverse stelle per questo gruppo. Abbiamo scoperto che quando cambiamo il contingente del gruppo, la datazione di Arturo può variare dallo 0 d.C. fino al 1000 d.C., vale a dire che i risultati possono fluttuare in uno spazio di mille anni. E' proprio questa circostanza che invalida completamente il metodo offerto da Y. N. Yefremov.
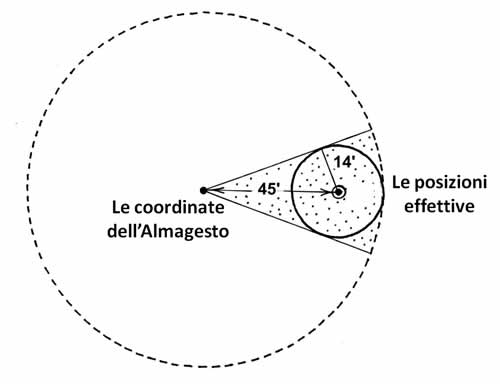
Figura 3.13a.
Corollari:
1. Il risultato della datazione dell'Almagesto attraverso i moti propri delle stelle, sostenuto da Y. N. Yefremov e Y. D. Pavlovskaya in [273] e [274], si basa su aria fritta. Inoltre, alcune delle considerazioni che si trovano nei loro lavori sopracitati, contengono un “circolo vizioso”.
2. Se dovessimo privare le opere in questione ([273] e [274]) da tutte queste considerazioni “circolari”, la “discrepanza” che finiremmo per ottenere non sarebbe in contraddizione con la nostra datazione, vedi più avanti.
3. Le posizioni di Y. N. Yefremov e Y. D. Pavlovskaya riguardo le stime di precisione del loro metodo (e il modello di correzione dell'Almagesto) che si vedono in [273] e [274], a nostro avviso sono matematicamente ignoranti e prive di significato.
4. Per qualche “ragione sconosciuta”, gli autori di [273] e [274] non hanno preso in considerazione Procione, la quale offre una datazione palesemente anti scaligeriana.
Il lavoro di Y. N. Yefremov e Y. D. Pavlovskaya ([273]) è stato pubblicato nel 1987 sulla Doklady Akademii Nauk SSSR. Abbiamo sottolineato gli errori contenuti in [273] e [274] nei nostri articoli [350] e [355] pubblicati sulla Doklady Akademii Nauk SSSR rispettivamente nel 1989 e nel 1990. A parte questo, ci siamo rivolti personalmente a Y. N. Yefremov criticando i suoi errori presso il seminario ospitato dall'Istituto di Storia della Tecnica e delle Scienze Naturali nel 1989. Yefremov non ha fatto nulla per correggere gli errori in questione; inoltre, fugge da tutti i tentativi di discutere l'argomento.
4.5. La stima di precisione errata dei calcoli astronomici: un altro esempio.
Consideriamo un'altra pubblicazione che affronta il problema della datazione dell'Almagesto ([179]). I suoi autori, Y. S. Goloubtsova e Y. A. Zavenyagin, fanno riferimento a Galley riportando che nel tempo trascorso tra Tolomeo e Galley (fino al 1690, quando fu creato il catalogo stellare di Flamsteed), Arturo si è spostata nella direzione della Vergine di 1,1 gradi. Dopo aver confrontato questo dato con il valore dello spostamento annuale di Arturo (2,285"), la Goloubtsova e Zavenyagin eseguono il seguente semplice calcolo, scrivendo che “se lo dovessimo dividere 1,1 gradi per i 2, 285 secondi angolari per anno, finiremmo per ottenere 1733 anni. Alla fine, una volta sottratto 1733 da 1690 (ovvero l'anno in cui fu compilato il catalogo di Flamsteed), arriveremmo alla conclusione che il catalogo dell'Almagesto fu compilato nel 43 a.C. Il tasso di errore della discrepanza per le coordinate delle stelle vicine è molto più piccolo dell'errore delle coordinate effettive, poiché la sottrazione rimuove l'errore sistematico. Pertanto, il tasso medio di errore nelle posizioni delle stelle luminose in relazione a quelle vicine, nell'Almagesto non supera gli 0,1 gradi [? - autore]. L'implicazione è che il possibile tasso di errore della datazione non superi i 150 anni” ([179], pagina 75).
Pertanto, se gli autori di [273] hanno datato il catalogo al 250 d.C. per mezzo di Arturo (persino dopo aver eseguito il loro “adattamento” al 310 d.C., la stima di precisione è pari a ± 360 anni), gli autori di [179] eseguono un unico e solo calcolo aritmetico e datano l'Almagesto al 43 d.C., sempre tramite Arturo, con un tasso di precisione molto maggiore di ±150 anni.
Tuttavia, il testo citato sopra e preso da [179] è orientato a un lettore che non si preoccuperà mai di controllare la vera configurazione stellare sulla sfera celeste. I calcoli degli autori di [179] sono basati sulla tacita implicazione che il vettore movimento dell'odierna Arturo è diretto esattamente alla sua posizione nell'Almagesto. Se fosse davvero così, i loro calcoli avrebbero dietro una sorta di ragionamento. Tuttavia, questo non sembra essere il caso. Nella Figura 3.1 si vede la vera direzione del moto di Arturo in relazione alla sua posizione come specificata nell'Almagesto.
Si può chiaramente vedere che Arturo si sposta visibilmente “a fianco” della sua posizione nell'Almagesto. Pertanto, non è il valore di 1,1 gradi che deve essere diviso per 2", come hanno fatto gli autori di [179] per qualche motivo, ma uno molto più piccolo che produrrà la datazione del 900 d.C. circa, anche se con un possibile tasso di errore significativo dovuto alla natura approssimativa del metodo stesso. Sopra potete vedere le nostre considerazioni sulla precisione di questo metodo.
Quindi, datare l'Almagesto al 43 d.C. con un possibile tasso di discrepanza di ±150 anni, come affermano di avere fatto Y. S. Goloubtsova e Y. A. Zavenyagin, è completamente fuori discussione.
Vi facciamo anche notare che il “concetto” stesso che sta dietro a [179], il quale implica che gli errori casuali nell'Almagesto sono il risultato del moto proprio delle stelle, è perfettamente sbagliato. La sua assurdità diventerebbe più evidente se dovessimo considerare gli esempi delle stelle che si muovono lentamente, che sono quasi immobili. La divisione di un errore diverso da zero nell'Almagesto sulla posizione di una stella, potrebbe produrre una qualsiasi datazione “infinitamente antica” delle osservazioni.
L'affermazione fatta dagli autori di [179] i quali dicono che l'errore sulle posizioni delle stelle luminose nell'Almagesto non supera gli 0,1 gradi, o i 6', non si basa su nulla. Perché 6' e non 2' o 15'? Dopo aver detto tutto sul problema della stima di precisione delle coordinate stellari nell'Almagesto, riteniamo superfluo approfondire questo problema.
Gli autori di [179] non hanno limitato le loro ricerche allo studio di Arturo e al suo comportamento. Hanno anche tentato di datare il catalogo con un'altra famosa stella “veloce”: Procione. Citiamo: “Otterremo un risultato simile una volta che dateremo l'Almagesto con il moto proprio di Procione, vale a dire che il catalogo dell'Almagesto fu compilato nel 330 a.C., con un possibile tasso di errore di ±300 anni ... La datazione di Procione serve per corroborare la datazione perfettamente indipendente di Arturo e ci portano entrambi negli ultimi secoli prima della nuova era” ([179], pagine 75-76).
Tuttavia, proprio come avevano fatto nel caso di Arturo, per qualche motivo gli autori non tennero conto della direzione del moto di Procione. Vediamo che “datazione” otterremmo se dovessimo usare il loro “metodo” per i nostri calcoli precisi che prendono in considerazione le posizioni stellari effettive. Si scopre che la vera traiettoria del moto di Procione è tale che la datazione approssimativa di Procione è il X secolo d.C., non prima (vedere il paragrafo 1). Inutile dire che il problema della precisione di questa datazione resta ancora in piedi.
4.6. La “analisi secondaria” della datazione dell’Almagesto nella rivista Samoobrazovaniye (Autodidattica).
Nel primo numero del 1999 della rivista moscovita Samoobrazovaniye ([263]) troviamo una pubblicazione di A. S. Doubrovskiy, N. N. Nepeyvoda e Y. A. Chikanov intitolata A proposito della cronologia dell'Almagesto di Tolomeo. Un'analisi matematica e metodologica secondaria che si occupa in particolare della nostra datazione dell'Almagesto attraverso i moti propri delle stelle.
Sfortunatamente, gli autori di [263] non sono riusciti a familiarizzare con le necessarie questioni astronomiche e quindi sono arrivati alla falsa conclusione che la datazione dell'Almagesto attraverso i moti propri delle stelle è in linea di massima inaffidabile, in quanto si sa poco e male delle velocità dei moti propri delle stelle, che presumibilmente riflettono le grandi controversie che si possono trovare nella letteratura astronomica.
Inoltre, in [263] abbiamo trovato una tabella comparativa dei moti propri tratta dal Astronomicheskiy Yezhegodnik (L'Annuario Astronomico) e dal catalogo di [1197]. Ad esempio, il lettore viene invitato a confrontare i valori contenuti rispettivamente in entrambi i cataloghi (-0.1098; -0.2001) e (-1.155; -1.998). Queste sono le velocità del moto proprio di Arturo.
A questo proposito gli autori di [263] ci dicono esattamente quanto segue: “Per quanto riguarda l'analisi del moto della stella “veloce”, dobbiamo sottolineare che i dati relativi alla velocità stellare presi dal catalogo dal gruppo di Fomenko ... [seguito da un riferimento al catalogo delle stelle luminose (1197) - autore] differiscono considerevolmente da quelli contenuti nel Astronomicheskiy Yezhegodnik” ([263], pagina 23).
Dopo aver citato questa considerevole tabella a pagina 24 di [263], gli autori giungono alla seguente conclusione: “Come si può vedere dalla tabella, stimare l'età del catalogo secondo i moti propri delle stelle è un'attività più che dubbia e che non regge alle critiche”.Tuttavia, i componenti del vettore velocità che vengono confrontati in questa tabella non solo sono stati forniti da sistemi di coordinate differenti, ma anche in unità di misure diverse! Questo è facile da osservare dall'esempio sopra: in un caso abbiamo a che fare con il sistema delle coordinate equatoriali per l'epoca del 2000 d.C., mentre nell'altro con il sistema delle coordinate equatoriali per l'epoca del 1900 d.C. Questi sistemi di coordinate differiscono l'uno dall'altro. L'esempio sopra dimostra un'incongruenza nella scala. Secondo il teorema di Pitagora, i componenti del vettore velocità forniti per Arturo sono sufficienti per il calcolo della lunghezza di detto vettore, il quale sarà già indipendente dal sistema delle coordinate. Tuttavia, nel primo caso è dieci volte più piccola che nel secondo e deriva dal fatto che i differenti cataloghi utilizzano delle diverse grandezze di moti propri. In un caso, l'unità di misura utilizzata è uguale a 1/1000 di secondo all'anno, mentre nell'altro è 1 secondo per secolo. Le unità differiscono di un fattore dieci.
Non è necessario fare dei commenti qui. E' ovvio che prima di suggerire al lettore di confrontare diversi valori di qualsiasi tipo, detti valori devono essere indicati nella stessa grandezza.
Ci asteniamo dal discutere i tentativi degli autori di datare l'Almagesto ([263]); diciamo semplicemente che siamo dell'opinione che la datazione dell'Almagesto deve essere preceduta da uno studio approfondito di alcune questioni piuttosto complesse da parte del ricercatore. La cosa richiede molto tempo e sforzo, persino per un esperto qualificato.
5. Conclusioni e indicazioni per ulteriori studi. Il nostro approccio e una breve sinossi dei nostri risultati principali.
5.1. I tre problemi con cui ci si deve confrontare: l'identificazione delle stelle dell'Almagesto, la definizione della natura dei possibili errori e l'analisi della precisione del catalogo.
I paragrafi 1-3 contengono i resoconti di numerosi tentativi di datare l'Almagesto sulla base del materiale numerico contenuto nel catalogo stellare di Tolomeo. Tutti questi tentativi si sono rivelati inutili. Ne abbiamo discusso così nei dettagli per due ragioni: in primo luogo, il lettore può avere un'idea migliore di quanto sia veramente complessa la datazione “autosufficiente” del catalogo stellare, vale a dire quel tipo di datazione che si basa solo sul materiale numerico del catalogo. In secondo luogo, abbiamo voluto fornire alcune basi per far crescere le questioni che affronteremo più dettagliatamente in seguito.
Il corollario principale a cui arriviamo nella fase attuale è il seguente. La datazione dell'Almagesto richiede una meticolosa analisi preliminare del catalogo. Questa analisi deve riguardare i seguenti problemi.
- Identificare le stelle dell’Almagesto con quelle osservabili sulla sfera celeste contemporanea. Nel paragrafo 1 abbiamo dimostrato che questo problema non ha sempre una soluzione inequivocabile; inoltre, la soluzione in questione potrebbe dipendere dalla presunta datazione del catalogo. Pertanto, prima di poter procedere con la datazione, dobbiamo trovare e rifiutare tutti i casi di dubbia identificazione delle stelle dell’Almagesto con loro odierne controparti.
- La natura dei possibili errori contenuti nel catalogo dell'Almagesto. I tassi di errore nelle caratteristiche delle coordinate stellari per l'Almagesto portano alla conclusione che la datazione del catalogo non può essere stimata con più precisione sull'intervallo storico basato sui moti propri delle stelle. Tuttavia, se riuscissimo a scoprire la componente sistematica negli errori sulle posizioni delle stelle dell'Almagesto, questa affermazione diventerebbe in linea di massima falsa. In questo caso potremmo avere un'opportunità per compensarla, aumentando così la precisione del catalogo che a sua volta potrebbe permetterci di datarlo a prescindere dall'errore in questione.
- La precisione del catalogo dell'Almagesto ottenuta attraverso diversi sottoinsiemi stellari. L'obiettivo di questa analisi è la scelta del gruppo stellare dell'Almagesto le cui coordinate devono essere state misurate da Tolomeo con un certo livello δ di precisione garantita. Una volta che riusciamo a individuare quel gruppo, questo definirà l'insieme delle possibili datazioni dell'Almagesto, vale a dire che renderebbe fattibili le datazioni che consentono di arrivare a un livello δ di precisione garantita per le stelle di questo gruppo. Se il risultante intervallo di datazione dovesse rivelarsi molto più breve dell'intervallo storico noto a priori, otterremmo delle informazioni pertinenti alla data di quando fu compilato il catalogo stellare dell'Almagesto. Questo concetto sarà usato più avanti (vedere i Capitoli 5-7).
Parliamo brevemente di ognuno dei tre problemi elencati sopra. Una loro interpretazione più dettagliata la potete trovare nei capitoli a seguire.
5.2. L’identificazione delle stelle dell’Almagesto.
C'è una quantità piuttosto grande di copie scritte a mano, come pure numerose versioni medievali stampate dell'Almagesto, dove le coordinate dell'eclittica delle singole stelle differiscono l'una dall'altra. La maggior parte di queste copie ed edizioni (sebbene non tutte) furono datate approssimativamente al 60 d.C. per mezzo della precessione. L'implicazione è che se si dovessero confrontare le longitudini stellari prese da una determinata copia dell'Almagesto con le longitudini stellari calcolate con precisione per il 60 d.C., il tasso medio di discrepanza sarebbe pari a zero. Tale confronto è possibile solo per il fatto che l'identificazione della maggior parte delle stelle dell'Almagesto con quelle dell'odierna sfera celeste, non lascia spazio a dubbi.
Il testo sorgente che abbiamo usato era il catalogo dell'Almagesto che contiene più di un migliaio di stelle, nella stessa forma esatta in cui viene riportato nell'opera fondamentale di K. Peters ed E. Knobel ([1339]). Nell'elenco delle stelle prese in esame sono state incluse numerose coordinate varianti prese da [1339]. Nella fase preliminare non abbiamo nemmeno dubitato della veridicità delle coordinate stellari dell'Almagesto, né dal fatto che fossero state ricavate dalle coordinate eclittiche riportate al 60 d.C. per via della precessione.
Come abbiamo già menzionato, [1339] contiene le identificazioni delle stelle dell'Almagesto con le odierne controparti. Tuttavia, abbiamo condotto il processo di identificazione partendo da zero per poter selezionare le stelle da analizzare, vedere il Capitolo 4. Per cui, le identificazioni contenute in [1339] sono state per la maggior parte confermate.
Tuttavia, abbiamo scoperto numerose stelle odierne che possono essere identificate con le diverse stelle dell'Almagesto per le epoche differenti di t. Come ad esempio o2 Eri e μ Cas. Queste stelle furono identificate in [1339] ipotizzando che le osservazioni di Tolomeo fossero condotte intorno all'inizio della nuova era. Non ha senso basare la datazione del catalogo dell'Almagesto sull'analisi di quelle stelle, perché finiremmo semplicemente in un circolo vizioso. Tutte queste stelle sono state escluse da ulteriori considerazioni.
Facciamo inoltre notare che le identificazioni e le coordinate delle stelle o2 Eri e μ Cas sono considerate dubbiose.
5.3. I vari tipi di errori nel catalogo.
Prima abbiamo dimostrato che il semplice confronto delle coordinate stellari calcolate con quelle contenute nel catalogo dell'Almagesto, non ci consente di stimare la datazione di quest'ultimo. Questo viene spiegato dagli enormi tassi di discrepanza insiti per la maggior parte nel catalogo dell'Almagesto. Pertanto, potremmo aver successo solo se analizzassimo meticolosamente gli errori dell'Almagesto di natura diversa.
Divideremo gli errori in tre tipi: gli errori di gruppo, gli errori casuali e i “refusi”.
Sotto gli errori di gruppo comprendiamo le varie distorsioni dei dati risultanti dalle osservazioni o dai ricalcoli che portano allo spostamento di un gruppo di stelle in un gruppo celeste nel suo insieme.
Gli errori casuali hanno un carattere individuale e devono la loro esistenza alle osservazioni imprecise che per la maggior parte rientrano nel grado di valore dello strumento di misurazione. Un tratto distintivo di questi errori è che spostano ogni stella sulla sfera celeste per un valore casuale che ha una media pari a zero.
I refusi sono il prodotto di circostanze impreviste o sconosciute al compilatore: errori di copia, rifrazione, ecc... Influiscono anche sulle coordinate delle singole stelle e i loro valori sono di solito molto più grandi della scala di precisione dello strumento di misurazione. I refusi sono un tipo di errore piuttosto raro.
Il compito più importante è quello di definire e compensare gli errori di gruppo. I metodi più idonei saranno discussi nel Capitolo 5, dove oltre a fornire le formule necessarie per il loro calcolo, dimostreremo anche come determinare la precisione dei valori risultanti.
Le stime dei diversi tipi di errori nelle coordinate stellari dell'Almagesto sono trattate nel Capitolo 6. Abbiamo scoperto che le coordinate stellari indicate nell'Almagesto contengono di fatto dei significativi errori di gruppo che si manifestano attraverso gli spostamenti delle rispettive configurazioni stellari sulla sfera celeste.
I valori degli errori di gruppo possono infatti differire per i diversi gruppi stellari: ad esempio le costellazioni, da cui il loro nome. Tuttavia testimonieremo che per quanto riguarda le aree celesti abbastanza grandi, gli errori di gruppo dell'Almagesto e degli altri vecchi cataloghi stellari, queste coincidono per le varie costellazioni e sono pari al singolo errore per l'intera area. Ci riferiamo a quel tipo di errore come quello sistematico per un determinato catalogo e per una determinata area celeste.
Ciascun spostamento che definisce un errore di gruppo può essere descritto da tre parametri. Sceglieremo i seguenti errori di base in quanto tali, vedi la Figura 1.1, Capitolo 1.
L'errore τ nel punto dell'equinozio di primavera Q(tA), eseguito dall'osservatore nell'anno di osservazione tA in direzione dell'eclittica. In altre parole, τ è la proiezione del punto dell'equinozio di primavera del catalogo dell'Almagesto, spostata lateralmente rispetto alla sua posizione effettiva sull'eclittica.
L'errore β nella posizione del punto Q(tA) nella direzione del meridiano, ovvero la proiezione del vettore errore sopra il meridiano dell'eclittica.
L'errore γ nell'angolo ε tra l'eclittica e l'equatore. Il cambiamento delle coordinate dell'eclittica di una stella fatto da terra dall'osservatore, deve essere preceduto dalla stima dell'angolo ε tra l'eclittica e l'equatore, a prescindere dal metodo di misurazione. Se l'osservatore ha commesso l'errore γ nella stima di detto angolo, l'eclittica del catalogo dovrà essere spostata per il valore di γ in relazione alla posizione dell'eclittica effettiva nell'anno di osservazione.
La possibilità che gli errori di gruppo possano essere inerenti all'Almagesto, è stata discussa da molti ricercatori; per esempio vedi [1339], [614] e [544]. Qui ci limitiamo semplicemente a citare le possibili ragioni dell'esistenza di tali errori.
L'errore τ potrebbe derivare dal fatto che l'osservatore o un successivo compilatore del catalogo, per qualche motivo ha “ritoccato” il catalogo per adattarlo a una datazione diversa da quella effettiva dell'osservazione. E' possibile che questa operazione sia servita per qualche fine metodologico: per esempio, conformare il catalogo a una data importante o ridondante. Avrebbe anche potuto essere usata per una deliberata distorsione della data effettiva di osservazione ([614]) o, in alternativa, potrebbe derivare dai cambiamenti nel punto iniziale del riferimento longitudinale. Abbiamo già dimostrato che gli astronomi antichi erano in grado contare la longitudine dai vari punti sull'eclittica. Il cambiamento del punto iniziale di riferimento porterebbe naturalmente all'aggiunta di qualche costante a tutte le longitudini dell'eclittica e quindi all'alterazione della “datazione” del catalogo, qualora fosse stato datato tramite la precessione longitudinale.
È comprensibile che la latitudine di una stella sia indipendente dall'errore τ. Questo crea delle coordinate latitudinali più affidabili, motivo per cui prenderemo in considerazione separatamente le longitudini e le latitudini. La considerazione delle discrepanze latitudinali richiede solo due parametri per definire un errore di gruppo, per esempio β e γ.
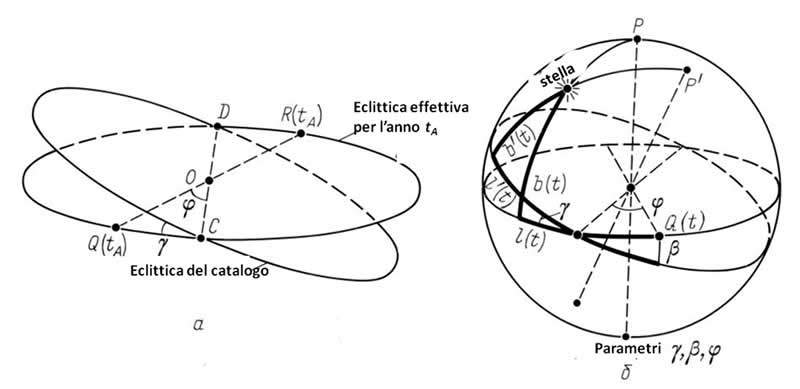
Figura 3.14. La specificazione dei parametri dell'errore sistematico nelle coordinate eclittiche delle stelle con l'aiuto dei parametri γ e ϕ, o γ e β. Nel presente esempio τ = 0.
Cosa c'è dire sui valori di β e γ? Le latitudini equatoriali delle stelle sono abbastanza facili da determinare con sufficiente semplicità e precisione dall'osservazione effettiva ([75]). Pertanto, ci si dovrebbe aspettare che l'errore β sia abbastanza piccolo per il momento dell'osservazione, a condizione che l'osservatore fosse abbastanza preciso. L'errore γ ha un carattere principalmente diverso. La determinazione della posizione dell'eclittica viene ottenuta dopo calcoli e osservazioni piuttosto complesse, vedere il Capitolo 1. Pertanto, il valore dell'errore γ potrebbe essere significativamente maggiore di quello dell'errore β.
Le opere [544] e [1339] contengono delle indicazioni sul fatto che l'errore sistematico γ è effettivamente inerente all'Almagesto. Inoltre, alcuni studiosi dell'Almagesto hanno stimato il valore di questo errore in circa 20'. I nostri calcoli lo confermano, vedere il Capitolo 6.
Utilizzeremo occasionalmente i parametri ϕ e γ al posto di β e γ, poiché sono più convenienti dal punto di vista del calcolo. Il loro significato viene chiarito nella Figura 3.14. Finché riguarda le discrepanze latitudinali, l'errore di gruppo si limita a un semplice spostamento del piano eclittico, che chiameremo “eclittica del catalogo”. Si potrebbe definire come la disposizione reciproca del piano dell'eclittica effettiva e dell'eclittica del catalogo per l'epoca tA di compilazione del catalogo, qualora si volesse fissare l'angolo ϕ tra l'asse dell'equinozio QR per l'epoca tA e l'asse del piano di rotazione CD, oltre a fissare l'angolo piano γ tra i due piani dell'eclittica: quello vero e quello falso. In seguito definiremo i parametri della maggior parte degli errori di gruppo con i valori di ϕ e γ.
In linea di massima, il compilatore del catalogo potrebbe aver commesso diversi errori di gruppo durante lo studio delle diverse aree celesti. Le possibili ragioni includono lo strumento di raggiustamento, la scelta di un diverso punto di osservazione, ecc...
Nel Capitolo 2 abbiamo scoperto le sette parti del catalogo stellare dell'Almagesto che ovviamente sono distintive come viste sulla sfera celeste e differiscono per le loro caratteristiche di affidabilità nell'Almagesto, vedi la Figura 2.14. Nel Capitolo 6 vedremo che le stesse aree celesti nell'Almagesto differiscono anche per i valori degli errori di gruppo e le caratteristiche di precisione.
Per riassumere, si può dire che le ragioni dell'esistenza degli errori di gruppo e delle altre discrepanze elencate sopra servono solo a spiegare i possibili meccanismi della genesi dell'errore. I calcoli consentono la scoperta degli errori stessi, ma non ci dicono nulla di come e perché sono stati fatti: le possibili ragioni possono differire per quanto detto in precedenza.
5.4. La scoperta dell'errore sistematico nel catalogo dell’Almagesto. La sua compensazione conferma la correttezza del catalogo di precisione dichiarato.
Il vero momento tA della compilazione del catalogo resta a noi sconosciuto. Pertanto, dovremmo calcolare i valori dei parametri γ(t) e ϕ(t). Il metodo di calcolo è una combinazione tra il metodo del minimo quadratico e il problema della regressione sferica. Le sue proprietà di precisione saranno discusse nel Capitolo 5.
I risultati dei nostri calcoli possono essere rappresentati nei grafici γstat(t) e ϕstat(t), vedi la Figura 3.15. Questi grafici furono costruiti dopo l'elaborazione delle coordinate stellari dell'Almagesto per le grandi aree celesti. L'indice “stat” indica che i valori corrispondenti sono stati edotti con i metodi statistici. In realtà sono delle stime dei parametri di discrepanza insiti nelle posizioni delle stelle dell'Almagesto e dimostrano che dette discrepanze sono uniformi per le numerosi grandi aree della sfera celeste. Le stime sono state fatte con l'assunto che il catalogo fu compilato nell'epoca t, per cui sono delle funzioni di t. Per l'errore in questione useremo il termine “errori sistematici”, così come per i suoi componenti, i parametri γ(t) e ϕ(t).
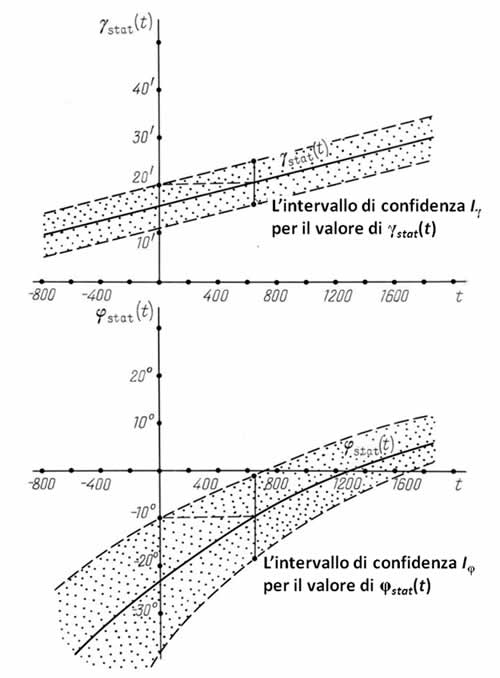
Figura 3.15. Il comportamento dei parametri γstat(t) e ϕstat(t) nel corso del tempo.
Qual è la relazione tra questi errori e gli errori di gruppo? Se la grande area celeste in fase di studio fosse costituita da diverse costellazioni, gli errori sistematici scoperti con l'aiuto dei metodi statistici rappresenterebbero i valori medi degli errori di gruppo per le diverse costellazioni. Solo nel caso in cui tutti gli errori di gruppo fossero uguali l'un l'altro, coinciderebbero con i rispettivi errori sistematici.
Questo è l'unico caso in cui non dovremo differenziare la definizione di “errore di gruppo” ed “errore sistematico”.
Abbiamo costruito gli intervalli di confidenza Iγ e Iϕ per i valori accettabili γ e ϕ attorno a ciascun valore di γstat(t) e ϕstat(t). Vogliamo chiarire che γstat e ϕstat sono solo delle stime statistiche puntuali di parametri sconosciuti; questi definiscono l'errore sistematico commesso dal compilatore del catalogo e i valori di tali stime non sono affatto uguali ai valori degli effettivi parametri sconosciuti. Una volta costruiti gli intervalli di confidenza attorno alle stime puntuali calcolate γstat e ϕstat, possiamo affermare che i veri valori del parametro rientrano in questi intervalli con un dato grado di certezza.
Il metodo di costruzione degli intervalli di confidenza che è ampiamente usato nei problemi statistici, è descritto nel Capitolo 5. I risultati effettivi pertinenti all'Almagesto sono stati riportati nel Capitolo 6.
Abbiamo condotto l'analisi degli errori per tutte e sette le aree celesti dell'Almagesto scoperte in precedenza, dopo aver determinato i valori dei loro rispettivi errori sistematici, nonché i valori delle “rimanenti” discrepanze latitudinali medie quadratiche risultanti dalla compensazione degli errori sistematici condizionali che sono stati scoperti. Di conseguenza, ciò che abbiamo scoperto è che le aree A e Zod A sono quelle che tra tutte sono state misurate con più precisione, vedi il Capitolo 6 e la Tabella 2.3. A proposito, queste sono le aree in cui si trovano la maggior parte delle stelle dell'Almagesto. Un'altra scoperta è stata quella che dopo la compensazione dell'errore sistematico, più della metà delle stelle dall'area A è finita con un valore massimo di discrepanza latitudinale di 10' (vedi Capitolo 6). La percentuale di quelle stelle “misurate bene” è ancora più grande per l'area Zod A: il 63,7%. Pertanto, il tasso di precisione dichiarato di 10' è stato confermato per le latitudini della maggior parte delle stelle di un'area celeste piuttosto grande.
Il successivo problema che ci siamo trovati di fronte è la natura dei parametri scoperti γstat e ϕstat. È vero che i valori calcolati di γstat e ϕstat sono abbastanza vicini agli effettivi errori di gruppo per l'intero catalogo, o almeno per le stelle dall'area A?
È del tutto possibile che il compilatore del catalogo abbia commesso dei singoli errori di gruppo per ciascuna costellazione; in questo caso, i valori che abbiamo calcolato di fatto rappresentano la somma delle varie medie degli errori di gruppo; il risultato di tali medie è diverso da zero a causa del numero relativamente piccolo delle costellazioni in generale.
Per rispondere a questa domanda, abbiamo considerato tutte le costellazioni zodiacali e i “dintorni” delle stelle più nominate. I calcoli hanno dimostrato che il valore di ![]() calcolato per l' area Zod A si applica come minimo a tutte le costellazioni dall'area A.
calcolato per l' area Zod A si applica come minimo a tutte le costellazioni dall'area A.
In altre parole, ![]() dovrebbe essere considerato come il componente sistematico che colpisce tutte le stelle misurate bene dell'area celeste A, la quale contiene anche la maggior parte delle stelle con nome. Tuttavia, non possiamo dire nulla riguardo il valore di
dovrebbe essere considerato come il componente sistematico che colpisce tutte le stelle misurate bene dell'area celeste A, la quale contiene anche la maggior parte delle stelle con nome. Tuttavia, non possiamo dire nulla riguardo il valore di ![]() . È curioso che la conclusione sulla natura dei composti γstat e ϕstat possa servire come argomentazione a favore della teoria che le misurazioni delle coordinate per il catalogo dell'Almagesto sono state condotte con l'uso della sfera armillare. Vedere il Capitolo 6 per maggiori dettagli.
. È curioso che la conclusione sulla natura dei composti γstat e ϕstat possa servire come argomentazione a favore della teoria che le misurazioni delle coordinate per il catalogo dell'Almagesto sono state condotte con l'uso della sfera armillare. Vedere il Capitolo 6 per maggiori dettagli.
5.5. La compensazione degli errori sistematici rilevati nel catalogo ci dà l'occasione di datarlo.
La compensazione dell'errore sistematico che abbiamo scoperto ci ha permesso di ridurre la discrepanza latitudinale per l'area Zod A dell'Almagesto, da 17,7' a 12,8'. La cosa ci ha dato la possibilità di datare il catalogo.
Abbiamo già sottolineato che il tasso di precisione dichiarato di 10 minuti è stato infatti raggiunto per la maggior parte delle stelle del catalogo. La domanda che sorge qui è: nell'Almagesto c'è qualche stella per la quale il tasso di precisione dichiarato potrà essere garantito?
Sappiamo che durante la misurazione delle coordinate stellari l'osservatore utilizza sempre il sistema dei punti di riferimento sulla sfera celeste (ossia le stelle), vedere [968], per esempio. Questo metodo di misurazione è naturale ed è stato usato da tutti gli astronomi medievali. Tycho Brahe, per esempio, per le sue misurazioni ha usato 21 stelle referenziali ([1049]). Il sistema moderno dei punti di riferimento è costituito da diverse migliaia di stelle che vengono raccolte nei cosiddetti cataloghi fondamentali (vedere il catalogo FK4, ad esempio - [1144]). Nell'Almagesto viene indicato che Regolo e Spiga devono far parte di quelle stelle referenziali. Ci sono dei paragrafi speciali dell'Almagesto che sono dedicati alla misurazione delle loro coordinate.
Formuliamo il seguente assioma. Se la precisione dichiarata del catalogo venisse confermata, dovrebbe essere garantita per la maggior parte delle stelle referenziali del catalogo in questione.
Quali sono le stelle che avrebbero dovuto essere necessariamente incluse nel numero delle stelle referenziali dell'Almagesto? Innanzitutto, Tolomeo deve aver usato quelle delle stelle che sul catalogo hanno un nome proprio. Non ci sono molte stelle di quel genere, solo dodici. Formano davvero una base molto utile nella parte visibile del cielo. La loro lista completa è la seguente: Arturo, Regolo, Spiga, Previndemiatrix, Capella, Lira = Vega, Procione, Sirio, Antares, Aquila = Altair, Aselli e Canopo; dodici stelle complessivamente.
Tutte queste stelle sono luminose e chiaramente visibili in cielo. Ciò che è particolarmente importante ai fini della datazione è che alcune di essi hanno una velocità di moto proprio piuttosto elevata, ad esempio Arturo, Procione e Sirio. Alcune altre attraversano persino la sfera celeste in modo abbastanza visibile, vale a dire Regolo, Capella, Antares e Aquila = Altair.
Tuttavia, abbiamo dovuto escludere da un'immediata considerazione due delle dodici stelle, vale a dire Canopo e Previndemiatrix. Il motivo è che le coordinate di Tolomeo per Canopo erano fortemente influenzate dalla rifrazione e da un punto di vista statistico potevano essere considerate come dei “refusi”; per quanto riguarda Previndemiatrix, le coordinate iniziali di Tolomeo sono andate perse, per cui a oggi sono semplicemente sconosciute, vedi il Capitolo 2.
Sono state scartate altre due stelle (Sirio e Aquila o Altair) a causa del fatto che, come mostra la nostra analisi, l'errore sistematico è differente nel loro caso e il valore di detto errore non può essere determinato per queste due stelle. Pertanto, la datazione del catalogo dell'Almagesto è stata realizzata sulla base delle restanti 8 stelle con nome. La loro lista è la seguente:
Arturo, 16, α Boo, numero di Bailey dell'Almagesto 110;
Regolo, 32, α Leo, numero 469;
Spiga, 67, α Vir, numero 510;
Capella, 13, α Aur, numero 222;
Lira = Vega, 3, α Lyr, numero 149;
Procione, 10, α CMi, numero 848;
Antares, 21, α Sco, numero 553;
Aselli, 43, γ Cnc, numero 452.
5.6. La datazione del catalogo dell’Almagesto per mezzo del moto delle sue otto stelle principali, dopo la rettifica dell'errore nel catalogo rilevato statisticamente.
L'ipotesi proposta ci conduce all'implicazione che per l'epoca desiderata tA della compilazione del catalogo, tutte e otto le stelle principali con nome dell'Almagesto devono avere una discrepanza latitudinale massima di 10'.
Figura 3.16.
La datazione del catalogo dell’Almagesto con il metodo statistico.
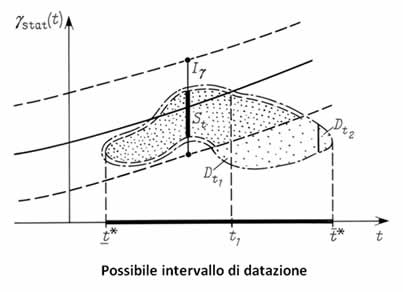
Figura 3.17.
La datazione del catalogo dell’Almagesto con il metodo geometrico.
D'altra parte, sappiamo che il componente sistematico di discrepanza γ del catalogo deve cadere nell'intervallo di confidenza Iγ, costruito attorno alla stima statistica γstat (tA) per epoca tA. Per cui siamo giunti a un metodo naturale di datazione.
Consideriamo l'intervallo di confidenza Iγ attorno a γstat(t) con il valore di t; il livello di confidenza viene fissato, quindi si seleziona un certo sottoinsieme St dai valori che cadono al suo interno, che compenserà il componente dell'errore sistematico γ e farà diventare inferiore a 10' la discrepanza latitudinale per tutte le otto stelle principali con nome, ovvero il grado di valore per la grandezza delle coordinate del catalogo dell'Almagesto con γ in St, vedere la Figura 3.16.
In linea generale, l'insieme St può essere vuoto. Mettiamo di trovare tutti i valori delle datazioni presunte t per le quali gli insiemi St non sono vuoti. Questi stessi valori devono essere compresi nel possibile intervallo di datazione, poiché per tutti le presunte datazioni t da questo intervallo, le latitudini di tutte e otto le stelle con nome vengono misurate con un tasso di precisione di 10'.
Chiameremo la procedura di datazione descritta con il termine “statistica”, poiché si basa sui valori di γstat (t) scoperti con i metodi statistici. Una più esplicita descrizione di questa procedura sarà riportata di seguito nel Capitolo 7, a fianco di una discussione dettagliata sui risultati di datazione ottenuti.
Abbiamo scoperto che l'intervallo di datazione inizia nel 600 d.C. e termina nel 1300 a.C. Anche se la sua lunghezza è pari a 700 anni a causa della bassa precisione dell'Almagesto, questo intervallo si trova a una distanza considerevole dalla datazione scaligeriana della creazione dell'Almagesto.
5.7. La datazione del catalogo dell’Almagesto dal moto delle sue otto stelle principali con nome, con l’aiuto di un metodo geometrico indipendente.
Gli intervalli di confidenza utilizzati per la procedura statistica contenevano un determinato parametro scelto soggettivamente, vale a dire il livello di confidenza che rappresenta una probabilità così minima da poter essere ignorata nei corollari statistici. Quindi si può effettivamente discutere la questione che l'intervallo di datazione è dipendente dal livello di confidenza prescelto. Il nostro corollario che l'errore di gruppo per le 8 stelle con nome è pari all'errore sistematico per l'area Zod A, è anche di natura statistica e può quindi risultare errato. Da qui la questione di quanto più grande possa diventare l'intervallo se le aree di confidenza si espandessero indefinitamente.

Figura 3.18. Il frontespizio di un'edizione del 1551 dell'Almagesto. In effetti, la data scritta a mano “Anno 1551” è degna di nota; è probabile che il libro sia stato datato retrospettivamente nel XVII-XVIII secolo.
Daremo una risposta “geometrica” a questa domanda. Selezioniamo ancora una volta un momento fisso t come candidato per il periodo di datazione desiderato. Dopodiché definiremo l'insieme Dt di quei valori γ che girando alla volta dell'eclittica effettiva tramite l’angolo per l'epoca t, faranno in modo che la discrepanza latitudinale di tutte le 8 stelle con nome si conformi alla soglia dei 10 minuti con un valore certo del parametro ϕ, vedere la Figura 3.17. È ovvio che Dt contiene un sottoinsieme St qualunque sia il valore di t. Pertanto, scopriremo tutti i possibili valori di t per i quali le latitudini di tutte e 8 le stelle con nome non devono differire dalle rispettive latitudini stellari indicate nell'Almagesto di oltre 10', dopo una certa rotazione dell'eclittica.
Un fatto ancor più importante è che il possibile e massimo intervallo geometrico di datazione risultante coincide con l'intervallo scoperto per mezzo dei metodi statistici. Vedere il Capitolo 7 per maggiori dettagli.
Un altro fatto che dimostreremo nel Capitolo 7 è che il metodo di datazione proposto possiede una certa stabilità non influenzabile dalla variazione dell'ipotesi iniziale, dalla precisione dichiarata del catalogo, dalla riduzione o espansione della datazione contingente alle stelle referenziali e anche alla distorsione dello strumento per le misurazioni non lineari.
La fattibilità del nostro metodo è stata anche testata sui cataloghi stellari compilati artificialmente come risultanti dal modellamento degli errori casuali nelle coordinate stellari delle osservazioni. In tutti i casi, le “date di osservazione” definite nel modellamento concordano con i risultati della datazione per mezzo del nostro metodo.
A parte questo, il metodo di datazione da noi offerto è stato testato con successo su numerosi vecchi cataloghi famosi. Lo abbiamo usato per datare i cataloghi di Ulugbek, Al-Sufi, Tycho Brahe ed Hevelius. In tutti i casi, le datazioni tradizionalmente conosciute dei vecchi cataloghi stellari in studio sono stati confermate dai nostri metodi; il catalogo dell'Almagesto è l'unica eccezione. A quanto pare, questa potrebbe essere un'indicazione che la datazione tradizionale della vita di Tolomeo contiene un gigantesco errore di diversi secoli o addirittura di oltre un millennio. Vedere il capitolo 9 per maggiori dettagli.
Il nostro corollario principale è il seguente. Il catalogo stellare dell'Almagesto fu creato nell'intervallo tra il 600 d.C. e il 1300 d.C. La datazione di Scaligero del catalogo dell'Almagesto (II secolo d.C.) è stata dimostrata ipso facto gravemente errata.
Concluderemo questo capitolo citando il frontespizio di un'edizione del 1551 dell'Almagesto (vedere la Figura 3.18). È molto curioso che la data di pubblicazione sia stata scritta a mano, esattamente nello stesso posto della pagina in cui ci si aspetta di trovare la data stampata. È possibile che questa data sia stata scritta sul libro alla fine del XVII o addirittura del XVIII secolo, probabilmente con lo scopo di far credere che il libro sia stato pubblicato nel XVI secolo, mentre la sua vera data di pubblicazione è molto più recente.