CAPITOLO 7
La datazione del catalogo stellare dell’Almagesto. Il metodo statistico e quello geometrico.
4. La datazione del catalogo dell’Almagesto tramite l’espansione del kernel informativo.
Il problema di espandere il kernel informativo dell'Almagesto è stato discusso in precedenza, alla fine del paragrafo 7.2. Abbiamo scoperto che se per questo scopo espandessimo il kernel scegliendo delle stelle luminose e veloci, senza seguire alcun sistema, non potremmo ottenere una datazione informativa. Abbiamo già capito che questo può essere spiegato dalla bassa precisione media delle misurazioni di Tolomeo e che questo riguarda anche le stelle luminose. La domanda su quale principio si potrebbe usare al fine di espandere il kernel informativo delle 8 stelle dell'Almagesto senza perdere la precisione latitudinale, rimane ancora aperta.
Siamo riusciti a risolvere questo problema. Riflettiamo sull'esatto metodo usato da Tolomeo per misurare la latitudine stellare. Si sa molto bene dalla storia dell'astronomia che quelle misurazioni furono condotte con una base di stelle luminose, usate come una sorta di “struttura” da cui edurre le posizioni stellari desiderate da tutte le misurazioni a seguire. Le coordinate di queste stelle sarebbero misurate con la massima precisione per poi essere usate in seguito. Tolomeo non specifica le stelle esatte che ha usato come base; come possiamo vedere dal testo dell'Almagesto, tra quelle stelle di base c'erano almeno Regolo, Spiga, Antares e possibilmente Aldebaran (vedere pagina 247 di [1120], per esempio). Tre di loro, vale a dire Regolo, Spiga e Antares, nell'Almagesto hanno un nome proprio con la formula “vocatur ...” (“con il nome di ...”), vedere i capitoli precedenti. Abbiamo formulato l'idea che le stelle con nome dell'Almagesto abbiano ricevuto i nomi innanzitutto perché servivano come base per le osservazioni di Tolomeo. Questa idea è stata confermata dal fatto che, come abbiamo dimostrato, le stelle con nome dell'Almagesto possiedono davvero la precisione tolemaica di riferimento di 10' (almeno quando vengono interessate le latitudini) nelle aree A, Zod A, B e Zod B. Questo non è vero per le longitudini, ma abbiamo già detto che è molto più difficile osservare le longitudini che le latitudini. Oltre a questo, la precisione longitudinale fu molto probabilmente persa quando il catalogo dell'Almagesto venne ricalcolato per farlo corrispondere ad altre epoche. Pertanto, le latitudini non possono servire da criterio della precisione effettiva di Tolomeo. Per questo scopo si può solo fare affidamento alle latitudini.
Non abbiamo potuto dimostrare nulla di quanto detto sopra per le altre regioni celesti, poiché i tassi dell'errore sistematico non possono essere stabiliti in modo affidabile. Pertanto, nella nostra ricerca delle possibili estensioni del kernel informativo ci asterremo dall'andare oltre le aree celesti A, Zod A, B e Zod B.
Domandiamoci: quali altre stelle eccetto quelle di base (ovvero quelle di “alto rango”) sono state misurate molto bene da Tolomeo? Ovviamente, quelle situate nelle immediate vicinanze delle stelle di base: il motivo principale è che le coordinate di Tolomeo molto probabilmente hanno seguito una sorta di “link”, poiché quando le coordinate delle stelle si avvicinavano a quelle di base venivano misurate per prime, dopodiché Tolomeo procedeva tenendo conto delle coordinate precedentemente calcolate, passo dopo passo. Oggi abbiamo capito che questo metodo di misurazione porta inevitabilmente a una crescita casuale della dispersione degli errori, il che significa molti più errori di misurazione nelle coordinate. Più lontana è una stella dal kernel di riferimento, peggio sarà misurata nella media.
Avrebbe quindi senso tentare di estendere il kernel informativo, aggiungendo le stelle che si sono “classificate come seconde”, ovvero quelle che sono abbastanza luminose, ben identificabili e situate in prossimità delle stelle di base. Si dovrebbe quindi procedere con le stelle più lontane di “terza categoria”, quelle di “quarta categoria” che sono ancora più distanti e così via. Se notassimo che questo processo è accompagnato da una lenta diminuzione della precisione media della latitudine, questa rimarrebbe praticamente la stessa per le stelle di base e quelle più vicine a loro, per cui dovremmo ipso facto confermare la nostra ipotesi che le stelle “prime in classifica” sono state davvero incluse nella struttura principale di riferimento. Avremmo anche l'opportunità di estendere il “kernel della datazione” del catalogo, come pure il controllo (e la possibile correzione) della nostra datazione.
Questa idea è stata implementata nel modo seguente. Prima di tutto dobbiamo usare solo le stelle dell'Almagesto perfettamente logiche, identificabili in modo affidabile e con un moto proprio osservabile. Sono state elencati nella Tabella 4.3. In totale sono 68 stelle. Tenete a mente che le 8 stelle del kernel informativo sono incluse tutte in questo elenco.
Sono state prese le otto stelle del kernel informativo per rappresentare il “livello più alto”. Abbiamo calcolato l'aberrazione latitudinale media quadratica di tutte, dopo la compensazione dell'errore sistematico. L'errore sistematico γ è stato calcolato nel Capitolo 6. Abbiamo permesso una fluttuazione del valore di questo errore entro un intervallo di ± 5', con un passo di 1 minuto. Il parametro β definisce gli eccessi entro i limiti di ± 20', con uno stesso valore del passo. La discrepanza media quadratica per ogni presunta datazione del catalogo è stata selezionata come il valore minimo raggiunto da dette variazioni dei parametri γ e β. Il risultato viene presentato con il grafico di dipendenza della discrepanza media quadratica della presunta datazione dell catalogo dell'Almagesto. Il grafico costruito per le otto stelle del kernel informativo, ovvero le stelle di “livello più alto”, si può vedere nella Figura 7.12.
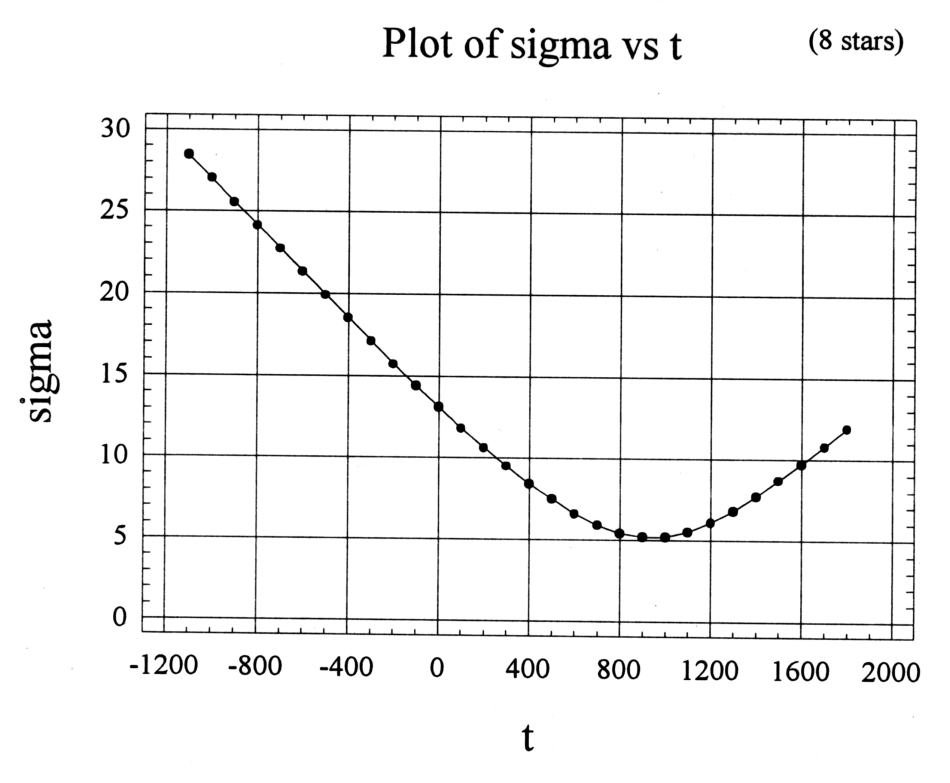
Figura 7.12.
Il grafico della discrepanza latitudinale media quadratica delle 8 stelle
di "primo livello", dopo la compensazione dell'errore sistematico.
Queste otto stelle formano il kernel informativo
del catalogo dell'Almagesto.
Secondo i nostri calcoli, queste stelle sono servite
da punti di riferimento per le osservazioni di Tolomeo.
La discrepanza media quadratica è stata minimizzata in conformità
con le variazioni del parametro γ per l'intervallo di γstat ± 5' e le variazioni
del parametro β per l'intervallo di 0 ± 20'.
Il grafico raggiunge il suo minimo nel 900-1000 d.C.,
nel livello di 5-6 grado d'arco.
La discrepanza equivale a 12' per l'epoca tolemaica del I secolo d.C.,
che supera il minimo di un fattore di due.
La discrepanza per l'epoca di Ipparco (II secolo a.C.)
equivale approssimativamente a 14'.

Figura 7.13.
Il grafico della discrepanza latitudinale media quadratica dopo
la compensazione dell'errore sistematico per le nove stelle
di "secondo livello" situate a una distanza massima
di 5 gradi da quelle di base.
La discrepanza media quadratica è stata ridotta al minimo
in conformità con le variazioni del parametro γ per l'intervallo
di γstat ±5' e le variazioni del parametro β per l'intervallo di 0 ± 20'.
Il grafico raggiunge il suo minimo nel 1000-1100 d.C.,
nel livello dei 9-10 gradi d'arco.
La discrepanza media quadratica equivale a 15' almeno
per l'epoca del II secolo d.C. e quelle che l'hanno preceduta.
Il minimo del grafico è stato raggiunto intorno al 900-1000 d.C., nel livello dei 5-6 gradi d'arco. Ciò significa che la precisione della misurazione latitudinale garantita da Tolomeo era pari a 10'-15'. Infatti, come abbiamo già fatto notare, tutte le stelle del kernel informativo sono state misurate con una precisione di 10' o persino migliore. Questo è in perfetto accordo con il valore del grado della scala di 10' scelto da Tolomeo.
Per quanto riguarda l'epoca del II secolo d.C., la discrepanza qui arriva a 12'. Si tratta di due volte il valore minimo consentito, che rende i primi anni dell'epoca dopo Cristo completamente inaccettabili per il catalogo dell'Almagesto, per non parlare della “epoca di Ipparco” che si suppone lo abbia preceduto, in quanto la discrepanza per il II secolo a.C. corrisponde a circa 14'.
Tutte le stelle della Tabella 4.3 sono state prese come stelle di “secondo livello” in quanto non sono più lontane di 5 grado dalle stelle del kernel informativo. Sono state trovate 9 stelle di questo tipo incluse quelle del kernel informativo. Abbiamo scoperto di dover aggiungere la stella 47δ Cnc (la n. 3461 nei cataloghi BS4 e BS5). Il risultante grafico della discrepanza media quadratica lo potete vedere nella Figura 7.13. È chiaramente visibile che l'immagine cambia drasticamente quando aggiungiamo una sola stella alle otto che formano il kernel informativo, sebbene si tratti solo di una che è molto vicina alle otto e ben visibile ad occhio nudo. Il motivo più probabile è che le stelle con nome furono usate da Tolomeo come riferimento e quindi vennero misurate più volte con la massima precisione. Le restanti devono essere state misurate “seguendo il collegamento” da una stella referenziale.

Figura 7.14.
Il grafico della discrepanza latitudinale media quadratica
dopo la compensazione dell'errore sistematico
per le dodici stelle di “terzo livello" situate
a una distanza massima di 10 gradi da quelle di base.
La discrepanza media quadratica è stata ridotta
al minimo secondo le variazioni del parametro
γ per l'intervallo di γstat ±5' e le variazioni
del parametro β per l'intervallo di 0 ± 20'.
Il grafico raggiunge il suo minimo nel 900 d.C., nel livello degli 11'.
La discrepanza equivale a più di 14' per l'epoca
del 100 d.C. e quelle che l'hanno preceduta.
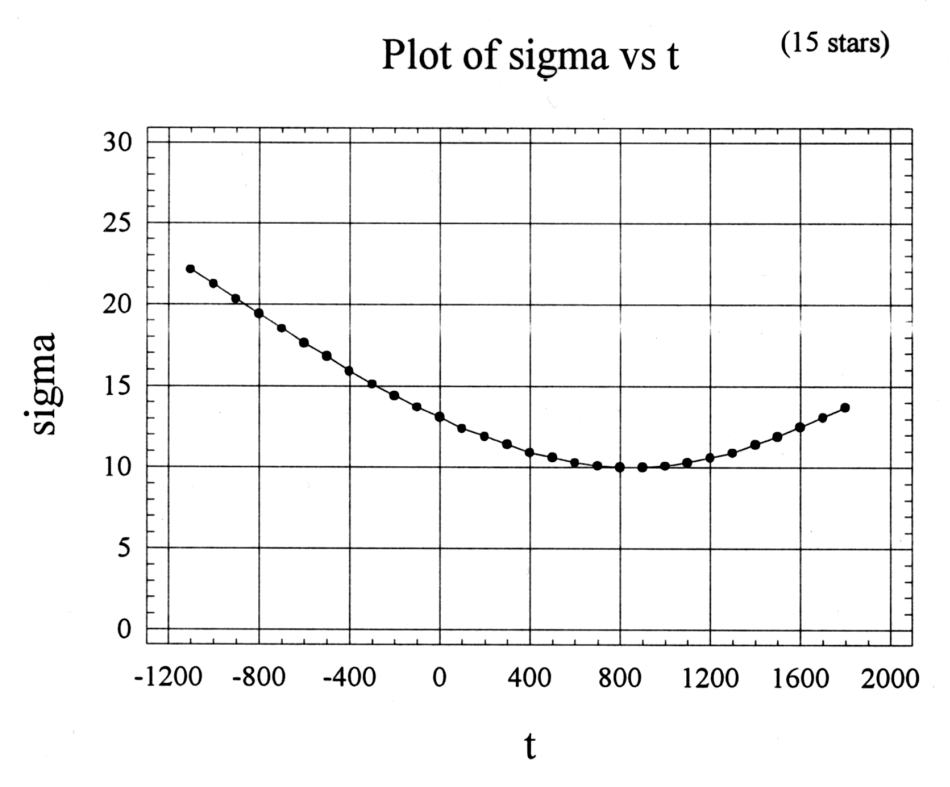
Figura 7.15.
Il grafico della discrepanza latitudinale media quadratica
dopo la compensazione dell'errore sistematico per le quindici stelle di “quarto livello” situate a una distanza massima
di 15 gradi da quelle di base.
La discrepanza media quadratica è stata ridotta al minimo secondo
le variazioni del parametro γ per l'intervallo di γstat ±5 'e le variazioni
del parametro β per l'intervallo di 0 ±20'.
Il grafico raggiunge il suo minimo nel 800-900 d.C.,
nel livello dei 10-11'.
La discrepanza per l'epoca del 100 d.C. è pari a 12'.
Ciò nonostante, il grafico che incontriamo nella Figura 7.13 è ancora abbastanza informativo. Il minimo del grafico della discrepanza è stato raggiunto intorno al 1000-1100 d.C., nel livello dei 9-10 gradi d'arco. La discrepanza media quadratica è sostanzialmente maggiore per l'epoca del II secolo d.C. così come per quelle che l'hanno preceduta. Equivale a 15' per il 100 d.C., che è sostanzialmente più grande del 150% del valore minimo.
Le stelle di “terzo livello” sono tutte stelle prese dalla Tabella 4.3 e che si trovano a una distanza massima di 10 gradi dal kernel informativo. Abbiamo scoperto che incluse nel kernel informativo ci sono 12 stelle di questo tipo. Oltre a 47δ Cnc, il kernel informativo è stato ampliato per includere 14o Leo (nr. 3852), 8η Boo (nr. 5235) e 26ε Sco (nr. 6241).
Il grafico della discrepanza è stato mostrato nella Figura 7.14. Difficilmente differisce da quello del passaggio precedente, ed è facile da capire il perché. Siamo ancora molto vicini al kernel informativo, che comprende ancora i 3/4 della quantità totale di stelle del campione. Il minimo del grafico è stato raggiunto nel 900 d.C., ossia nel livello degli 11'. La discrepanza per l'epoca del 100 d.C. e quelle prima equivale a 14' o più. A giudicare dalla Figura 7.14, la datazione più possibile del catalogo dell'Almagesto è l'intervallo tra il presunto 400 e il 1400 d.C.
Abbiamo preso tutte le stelle del “quarto livello” dal Tabella 4.3. Sono quelle stelle situate a una distanza massima di 15 gradi dal kernel informativo. Ci sono 15 di quelle stelle: le nuove aggiunte sono 78β Gem (nr. 2990), 79ζ Vir (nr. 5107) e 24μ Leo (nr. 3905). Il grafico di discrepanza può essere visto nella Figura 7.15. Il minimo del grafico è stato raggiunto intorno al 800-900 d.C., nel livello dei 10'-11' . La discrepanza per l'epoca del 100 d.C. equivale a 12'. Pertanto, il valore minimo della discrepanza media quadratica non si altera affatto. A quanto pare, per le distanze inferiori a 15° gli strumenti di Tolomeo consentivano comunque di misurare le coordinate stellari rispetto alle effettive stelle di base e non “seguendo i collegamenti”.

Figura 7.16.
Il grafico della discrepanza latitudinale media quadratica
dopo la compensazione dell'errore sistematico per le ventidue
stelle di "quinto livello" situate a una distanza massima
di 20 gradi da quelle di base.
La discrepanza media quadratica è stata ridotta al minimo
secondo le variazioni del parametro γ per l'intervallo di γstat ±5'
e le variazioni del parametro β per l'intervallo di 0 ±20'.
Il grafico raggiunge il suo minimo nel 400-800 d.C.,
nel livello dei 22-23'.
Questo è il livello che in linea generale
consideriamo caratteristico del catalogo dell'Almagesto.
In altre parole, la vicinanza delle "stelle di base"
cessa di essere efficace a una distanza di circa 15-20 gradi.
Il grafico è diventato quasi uniforme a causa
della riduzione significativa della precisione dei calcoli
a quella distanza dalle stelle di base.
La discrepanza equivale a 23' per l'inizio della nuova era,
24' per l'epoca del V secolo a.C., e così via.
Infine, per le stelle di “quinto livello” abbiamo preso quelle incluse nella Tabella 4.3, situate a una distanza massima di 20 gradi dal kernel informativo. Ci sono 22 stelle incluso il kernel informativo: le nuove arrivate sono 112β Tau (nr. 1791), 60ι Gem (nr. 2821), 68δ Leo (nr. 4357), 29γ Boo (nr. 5435), 3β CrB (nr. 5747) e 5α CrB (nr. 5793).
Il grafico della discrepanza è stato mostrato nella Figura 7.16. Il minimo del grafico è stato raggiunto intorno al 400-800 d.C., nel livello dei 22'-23'. Questo è livello dell'errore medio quadratico che è in linea di massima caratteristico del catalogo dell'Almagesto, vale a dire che l'effetto della vicinanza delle stelle di base cessa di manifestarsi a una distanza di 15° - 20°. Il grafico diventa quasi uniforme anche a causa di una visibile diminuzione della precisione di misurazione. La discrepanza equivale a 23' per l'inizio della nuova era, 24' per l'epoca del V secolo a.C. e così via.
L'ultimo passaggio mostra un drastico calo di precisione nelle misurazioni. Il tasso di errore medio quadratico è cresciuto per un fattore di due. Pertanto, prima di proseguire con la nostra estensione del kernel informativo del catalogo, ci impegniamo a calcolare la discrepanza media quadratica utilizzando solo quelle stelle di riferimento che ottengono un errore latitudinale massimo di 30 minuti per la presunta datazione del catalogo dell'Almagesto. Questo ci permetterà di escludere la stella che Tolomeo misurò peggio dall'inizio. La scelta di tali stelle dipende ovviamente dalla presunta datazione del catalogo. Certe presunte datazioni potrebbero far sembrare misurata bene una stella e male un'altra, e viceversa.
Continueremo a compensare l'errore sistematico rilevato nel catalogo dell'Almagesto e a far fluttuare sia γ che β nello stesso intervallo come sopra.
La quantità di stelle che ritroviamo nel campione dopo la selezione, sarà rappresentata sullo stesso grafico con la discrepanza. L'immagine risultante può essere vista nella Figura 7.17. Si può vedere che il minimo della discrepanza media quadratica scende di nuovo a 9' per il periodo 800-900 a.C., dove l'epoca scaligeriana di Tolomeo e Ipparco, ossia il 400 a.C. - 100 d.C. mostra i valori massimi della discrepanza raggiungendo persino i 12'. Facciamo notare che i risultanti valori di discrepanza di 9' per il presunto periodo di datazione del 800-900 d.C. si correla molto bene con il limite di discrepanza di 30' precedentemente specificato. La questione è che il valore casuale normalmente distribuito con la discrepanza media quadratica di circa 9'-10' è probabile che rimanga entro i limiti di 30' o 3σ e il tasso di probabilità è vicino a 1.
Espandiamo ora la distanza massima tra le stelle e il kernel informativo del catalogo da 20° a 25°. Considereremo ancora solo le stelle il cui errore latitudinale non supera i 30' per la presunta datazione in questione. Vedere i grafici risultanti nella Figura 7.18 che rappresenta la discrepanza e la quantità di stelle incluse nel campione per ogni presunta datazione. Il minimo della discrepanza media quadratica è stato raggiunto nell'intervallo tra l'800 e il 1000 d.C. ed è pari a circa 9,5'. Il tasso di discrepanza massima è approssimativamente pari a 12,5' ed è stato raggiunto circa nel 400 avanti Cristo. L'epoca scaligeriana di Tolomeo e Ipparco, ovvero l'inizio della nuova era, ha un tasso di discrepanza che si avvicina al massimo, circa 12'.
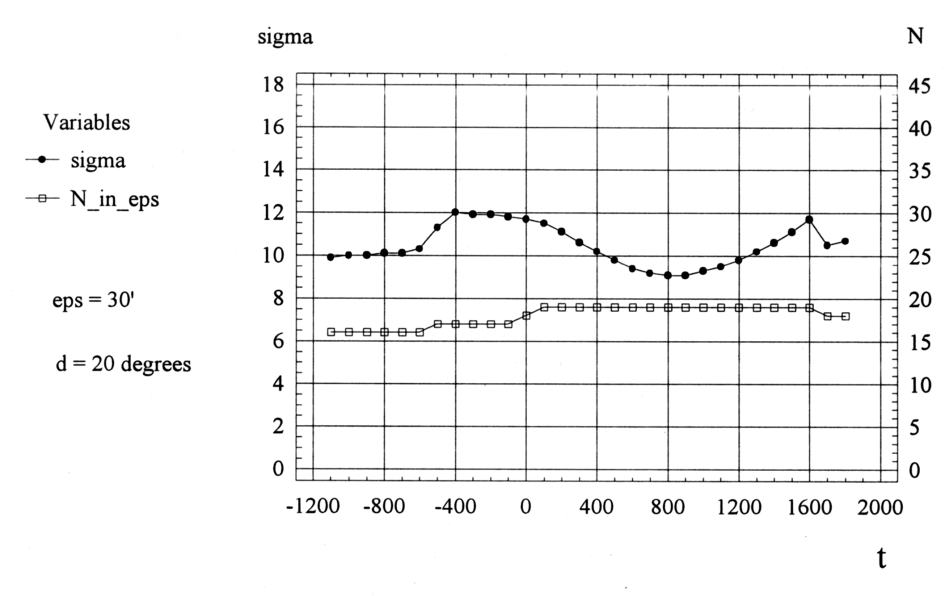
Figura 7.17.
Il grafico della discrepanza media quadratica per le stelle raccolte nella Tabella 4.3 e che si trovano entro i 20 gradi dalle stelle del kernel informativo del catalogo. Si può anche vedere il grafico del numero di stelle in questo gruppo. Le stelle la cui discrepanza latitudinale supera i 30 minuti per la presunta datazione in questione, sono state escluse dal campione. L'errore sistematico del catalogo è stato compensato.

Figura 7.18.
Il grafico simile della discrepanza latitudinale media quadratica per il gruppo di stelle della Tabella 4.3 situato entro 25 gradi
dalle stelle del kernel informativo del catalogo. Abbiamo anche presentato il grafico per il numero di stelle nel gruppo.
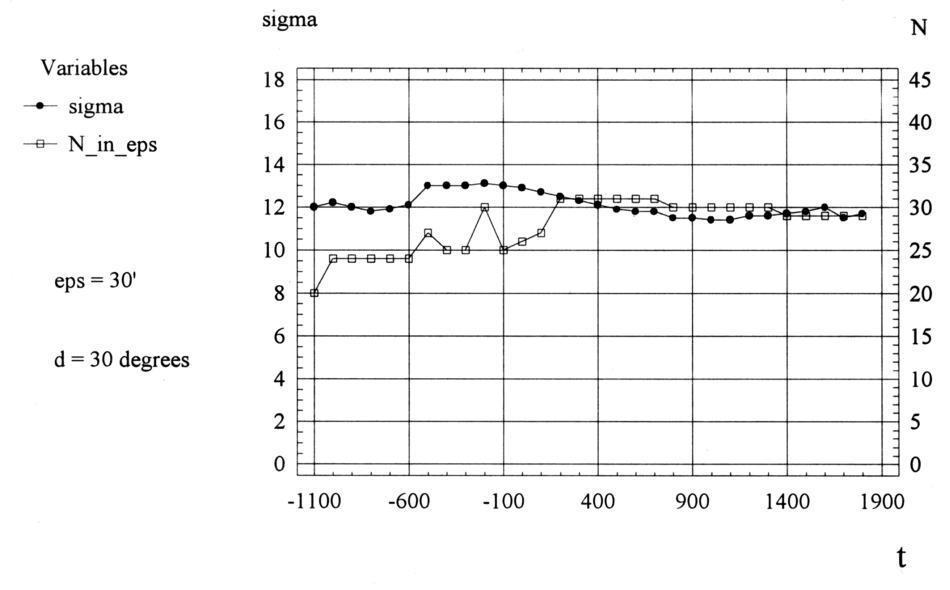
Figura 7.19.
Il grafico simile della discrepanza latitudinale media quadratica
per il gruppo di stelle della Tabella 4.3
situato entro 30 gradi dalle stelle del kernel informativo del catalogo.
Abbiamo anche presentato il grafico per il numero di stelle nel gruppo.

Figura 7.20.
Il grafico simile della discrepanza latitudinale media quadratica
per il gruppo di stelle della Tabella 4.3
situato entro 35 gradi dalle stelle del kernel informativo del catalogo.
Abbiamo anche presentato il grafico per il numero di stelle nel gruppo.
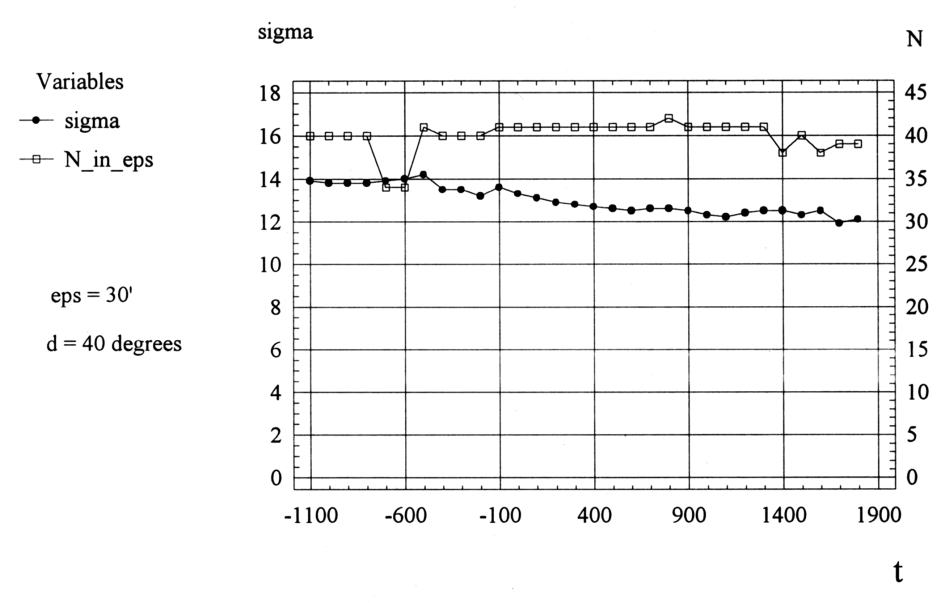
Figura 7.21.
Il grafico simile della discrepanza latitudinale media quadratica
per il gruppo di stelle della Tabella 4.3
situato entro 35 gradi dalle stelle del kernel informativo del catalogo.
Abbiamo anche presentato il grafico per il numero di stelle nel gruppo.
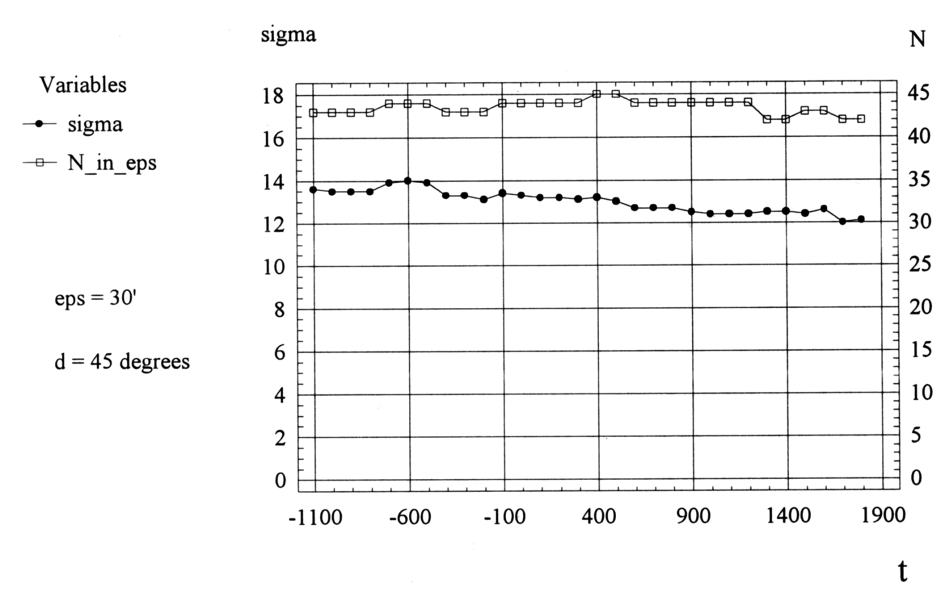
Figura 7.22.
Il grafico simile della discrepanza latitudinale media quadratica per il gruppo di stelle della Tabella 4.3 situato entro 35 gradi dalle stelle del kernel informativo del catalogo. Abbiamo anche presentato il grafico per il numero di stelle nel gruppo.
La quantità di stelle nel campione varia da 21 a 24. Nel campione ci sono 23 stelle corrispondenti alla discrepanza media quadratica minima.
Procederemo aumentando la distanza accettabile tra le stelle e il cuore da 25° a 30°, tenendo tutti gli altri parametri come erano prima. Il risultato può essere visto nella Figura 7.19. Ancora una volta, il minimo possibile della discrepanza latitudinale può essere raggiunto solo dopo l'800 d.C. Questo esempio contiene 30 stelle. La quantità di stelle nel campione varia tra 20 e 31 stelle, per diverse datazioni presunte. All'inizio della nuova era il tasso di discrepanza è approssimativamente pari a 13', che è vicino al valore massimo per il grafico in questione.
Nelle Figure 7.20, 7.21 e 7.22 si possono trovare i grafici simili per le stelle la cui distanza dal kernel del catalogo dell'Almagesto non supera rispettivamente i 35°, 40° e i 45°. Il campione è composto da circa 40 stelle. La discrepanza latitudinale media quadratica minima diventa meno manifesta e “va alla deriva verso il futuro”. In linea di massima, il grafico inizia a sembrare sempre più orizzontale.
Corollario. Quindi, il catalogo dell'Almagesto può essere datato dal moto proprio di una configurazione di circa 20 stelle. L'intervallo di datazione più possibile cade nella stessa epoca di cui sopra, vale a dire il 600-1200 d.C. Abbiamo anche scoperto che bisogna usare un'affidabile identificazione di quelle stelle che non si trovano a una distanza troppo grande dal kernel informativo (massimo 20° - 25°). Se dovessimo escludere le stelle che hanno un massimo di 30 minuti di discrepanza latitudinale per le presunte datazioni del campione, finiremmo con circa 20 stelle. Questo fornisce un grafico con un minimo che si manifesta molto bene, vedere la Figura 7.18. Il minimo di discrepanza latitudinale di 9' viene raggiunto nell'intervallo del 800-1000 d.C. L'intervallo del 600-1200 d.C. corrisponde a un tasso di discrepanza molto vicino al minimo, quello di 9' - 9.5'. L'epoca del 400 a.C. - 100 d.C. corrisponde al tasso di discrepanza massima di 11,5' - 12'.
Sottolineiamo che la minima discrepanza di circa 10' può essere raggiunto solo per un gruppo di alcune decine di stelle a condizione della loro vicinanza con il kernel informativo dell'Almagesto. Tutti gli altri metodi di selezione delle stelle dalle aree A, Zod A, B, Zod B e M associate per luminosità, “fama” ecc... ci lascia con una discrepanza minima di circa 20', che è tipico per l'Almagesto in generale. Anche restare all'interno di una singola area ben misurata (Zod A) non è un'opzione. Ad esempio, prendiamo in considerazione tutte le stelle visibilmente mobili di quest'area, cioè tutte le stelle della Tabella 4.3 che appartengono all'area celeste Zod A. Se non considerassimo il kernel informativo, ci sarebbero 12 stelle di quel genere; aggiungendo le 8 stelle alle 12 otterremmo un totale di 20 stelle. Sfortunatamente, la precisione di latitudine per questo elenco è piuttosto bassa, molto più bassa di quella dell'area Zod A in generale. Il corrispondente grafico della discrepanza latitudinale media quadratica per queste 20 stelle come funzione della presunta datazione del catalogo dell'Almagesto, può essere visto nella Figura 7.23. Il valore minimo che si è manifestato scarsamente corrisponde al livello dei 23' ed è stato raggiunto nell'intervallo tra il 400 e l'800 d.C.
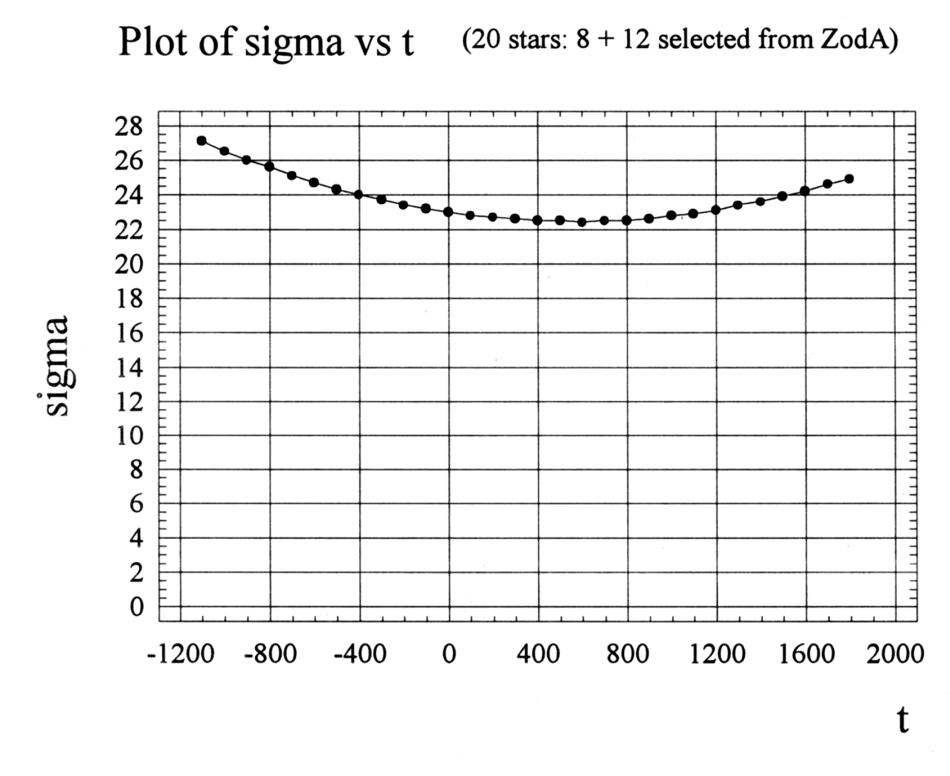
Figura 7.23.
Il grafico della discrepanza latitudinale media
quadratica per le 20 stelle: 12 stelle dalla Tabella 4.3
sono situate nella regione celeste Zod A,
le altre 8 sono quelle del kernel informativo del catalogo.
Come si può vedere dal grafico, la precisione
latitudinale per questo elenco è sostanzialmente
inferiore alla media per la regione Zod A.
Solo 1' sopra il minimo e copriremmo l'intero intervallo del 400 a.C. e il 1500 d.C. Perciò, questo elenco non consente alcuna datazione affidabile a causa della bassa precisione media delle latitudini stellari che contenuta in esso. Persino le otto stelle del kernel informativo non possono migliorare la precisione latitudinale media di questo elenco, a causa del fatto che la maggior parte delle stelle visibilmente mobili della regione Zod A sono piuttosto fioche e sono state quindi mediamente misurate male da Tolomeo. Tenete presente che la precisione media delle sue misurazioni latitudinali equivale a 12' -13' per l'intera area Zod A, che è molto meglio dei 23' che noi abbiamo per le 20 stelle in questione. Senza alcuna perdita sostanziale della precisione siamo quindi riusciti a espandere il kernel informativo dell'Almagesto nel gruppo delle 15 stelle identificabili attendibilmente e inequivocabilmente, che sono anche visibilmente mobili e la cui velocità annuale di moto proprio equivale a 0,1" per almeno una delle coordinate. La scelta del sistema delle coordinate celesti è di scarsa importanza ora, per cui, per questioni di comodità, abbiamo usato le coordinate equatoriali del 1900 d.C., poiché sono state utilizzate nei moderni cataloghi stellari che abbiamo utilizzato. Ora riportiamo l'elenco finale delle 15 stelle che consentono la datazione dell'Almagesto per mezzo del moto proprio delle stelle. Il numero BS4 della stella è indicato tra parentesi ([1197]).
1) 16α Boo (5340); 2) 13α Aur (1708); 3) 32α Leo (3982); 4) 10α CMi (2943); 5) 67α Vir (5056); 6) 21α Sco (6134); 7) 3α Lyr (7001); 8) 43γ Cnc (3449); 9) 78β Gem (2990); 10) 47δ Cnc (3461); 11) 14ο Leo (3852); 12) 24μ Leo (3905); 13) 79ζ Vir (5107); 14) 8η Boo (5235); 15) 26ε Sco (6241).
5. La datazione del catalogo dell’Almagesto per mezzo di una varietà di configurazioni formate da 8 stelle luminose.
L'idea alla base di questo calcolo e del calcolo stesso è da attribuire al professor Dennis Duke della State University della Florida, un eminente specialista nell'analisi dei dati. Ha suggerito di studiare tutte le possibili configurazioni delle otto stelle con nome dell'Almagesto.
Per questo scopo, il professor Duke ha scelto un set di 72 stelle la cui magnitudine dall'Almagesto è inferiore a 3 (tenete presente che più basso è il valore, più luminosa è la stella). Poi, da questo numero ha selezionato tutte le combinazioni di 8 stelle, il cui massimo errore latitudinale nel catalogo dell'Almagesto non supera i 10' per un certo intervallo temporale diverso da zero (t1, t2) che copre l'intero periodo tra il 400 a.C. e il 1600 d.C. Il totale è pari a 736 combinazioni di otto stelle su 500.000 possibilità. Ognuna di queste combinazioni di per sé specifica un intervallo di datazione (t1, t2). Il professor Duke ha studiato l'insieme dei “centri di intervallo di datazione”, ovvero l'insieme dei valori (t1 + t2) / 2. E' venuto fuori che se si dovesse costruire un istogramma di distribuzione delle frequenze di questi centri sull'asse del tempo, si vedrebbe manifestarsi il valore massimo nell'intervallo del 600-900 d.C., vedere la Figura 7.24. Perciò, l'epoca del VII-X secolo d.C. è la data più probabile in cui è stato compilato il catalogo dell'Almagesto.

Figura 7.24.
Istogramma di distribuzione della frequenza per “l'intervallo di datazione”
delle 736 configurazioni di 8 stelle luminose dell'Almagesto.
Si può vedere che il picco si manifesta nell'intervallo del 600-900 d.C.
L'approccio suggerito dal professor Duke ha il vantaggio che le configurazioni stellari misurate male o eccessivamente lente, vengono automaticamente escluse dal campione a causa del fatto che i loro intervalli di datazione o sono nulli per la soglia latitudinale di 10 minuti o abbastanza grandi da andare ben oltre l'intervallo storico del 400 a.C. - 1500 d.C. scelto a priori dal professor Duke. Si è scoperto che dopo questa rigida selezione rimangono ancora moltissime configurazioni, vale a dire 736 e ognuna di loro contiene otto stelle. Se dovessimo scegliere il “centro dell'intervallo di datazione” di alcune configurazioni con un livello latitudinale di 10', finiremmo con una datazione del catalogo che contiene alcuni errori casuali, oppure con una data di compilazione molto perturbata. Una volta creato il grafico di distribuzione di queste datazioni perturbate, saremo in grado di datare il catalogo dell'Almagesto con molta più precisione che nel caso in cui viene usata una singola configurazione.
L'ovvio presupposto è che la datazione effettiva del catalogo sia uguale al valore medio delle datazioni perturbate casualmente. Questa media può essere stimata dalla distribuzione empirica che abbiamo a nostra disposizione. Considerando che la distribuzione effettiva delle perturbazioni sia vicina alla normalità, sarà facile stimare la sua dispersione. L'aberrazione media quadratica della distribuzione selettiva che si vede nella Figura 7.24 equivale approssimativamente a 350 anni. Visto in che modo il campione è stato censurato in conformità a un intervallo temporale scelto a priori e che si è dimostrato asimmetrico rispetto al centro di distribuzione (vedere la Figura 7.24), la stima media per questa distribuzione risulta essersi spostata lateralmente. Se dovessimo prendere in considerazione questo effetto, la stima più precisa dell'aberrazione media quadratica dovrebbe produrre un valore ancora più piccolo.
Inoltre, il centro della distribuzione selettiva si trova vicino all'anno 800. Avendo un campione di elementi indipendente, si potrebbe arrivare alla conclusione che la datazione effettiva della compilazione del catalogo dell'Almagesto possa trovarsi all’interno di 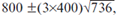 ossia 800 ± 45 anni. Tuttavia, il campione di elementi non può essere considerato indipendente, poiché la precisione effettiva dell'800 d.C. per la datazione dell'Almagesto è molto inferiore a ± 45 anni. Tuttavia, affermare in questa situazione che il periodo della compilazione del catalogo sia l'inizio dell'era dopo Cristo o un'epoca persino precedente, è una cosa da considerare altamente improbabile se non fuori discussione.
ossia 800 ± 45 anni. Tuttavia, il campione di elementi non può essere considerato indipendente, poiché la precisione effettiva dell'800 d.C. per la datazione dell'Almagesto è molto inferiore a ± 45 anni. Tuttavia, affermare in questa situazione che il periodo della compilazione del catalogo sia l'inizio dell'era dopo Cristo o un'epoca persino precedente, è una cosa da considerare altamente improbabile se non fuori discussione.
6. La procedura statistica per la datazione del catalogo dell’Almagesto: l’analisi della stabilità.
6.1. La necessità di utilizzare dei valori algoritmici variabili.
L'implementazione della procedura di datazione sopra descritta implica la scelta piuttosto arbitraria di alcuni valori che definiscono l'algoritmo, anche se gli altri valori derivano da conclusioni statistiche. Pertanto, nel caso in cui detti valori siano soggetti ad alterazione, occorre controllare il comportamento dell'intervallo di datazione.
6.2. La variazione del livello di confidenza.
Il valore di ε che determina il livello di confidenza è stato scelto piuttosto arbitrariamente. Tenete a mente che nei problemi statistici questo rappresenta il tasso di probabilità di accettabilità dell'errore; vale a dire che ε = 0.1 rappresenta la probabilità di un tasso di errore dello 0,1. Minore è il valore di ε, maggiore è l'intervallo di confidenza. La dipendenza delle dimensioni dell'intervallo di confidenza dal valore di ε è stata studiata nei Capitoli 5 e 6: in particolare, vedere la Tabella 6.3.
Consideriamo ora la variazione del nostro intervallo di datazione secondo ε. Abbiamo già detto che ogni valore di ε inferiore a 0,1 ci fornisce lo stesso intervallo di datazione del catalogo dell'Almagesto e lo si può vedere anche nella Figura 7.11. Questo risulta dalla posizione dell'intervallo St(α), dove α = 10'.
Tuttavia, vediamo che arriveremmo con un'immagine completamente diversa, qualora dovessimo scegliere un diverso valore di precisione garantita α che non sia uguale a quello di 10' dichiarato da Tolomeo. Consideriamo α uguale a 15' (vedere la corrispondente area ombreggiata nella Figura 7.11). Il possibile intervallo di datazione del catalogo dell'Almagesto si espanderà naturalmente. La soglia superiore dell'intervallo espanso non dipende da ε ed è uguale a t = 3, ossia il 1600 d.C. La soglia inferiore è solo marginalmente dipendente da ε, vale a dire che equivale a t = 16.3 per ε = 0, ossia il 270 d.C., mentre ε = 0,005 darà t = 16.5, in altre parole il 250 a.C.
Pertanto, questi risultati dimostrano che la scelta soggettiva del livello di confidenza ε non influenza il valore della soglia inferiore del possibile intervallo di datazione del catalogo dell'Almagesto.
Abbiamo anche scoperto in che modo la dimensione dell'intervallo di datazione viene influenzata dal valore di α il cui significato rappresenta la precisione della misurazione latitudinale delle stelle con nome del catalogo; in particolare, aumentando il valore del tasso di precisione dai 10' dichiarati da Tolomeo a 15', ossia aumentandolo di un fattore 1.5, il conseguente intervallo di datazione del catalogo dell'Almagesto non comprenderà l'epoca scaligeriana di Tolomeo, figuriamoci quella di Ipparco.
6.3. La riduzione del contingente del kernel informativo del catalogo dell’Almagesto.
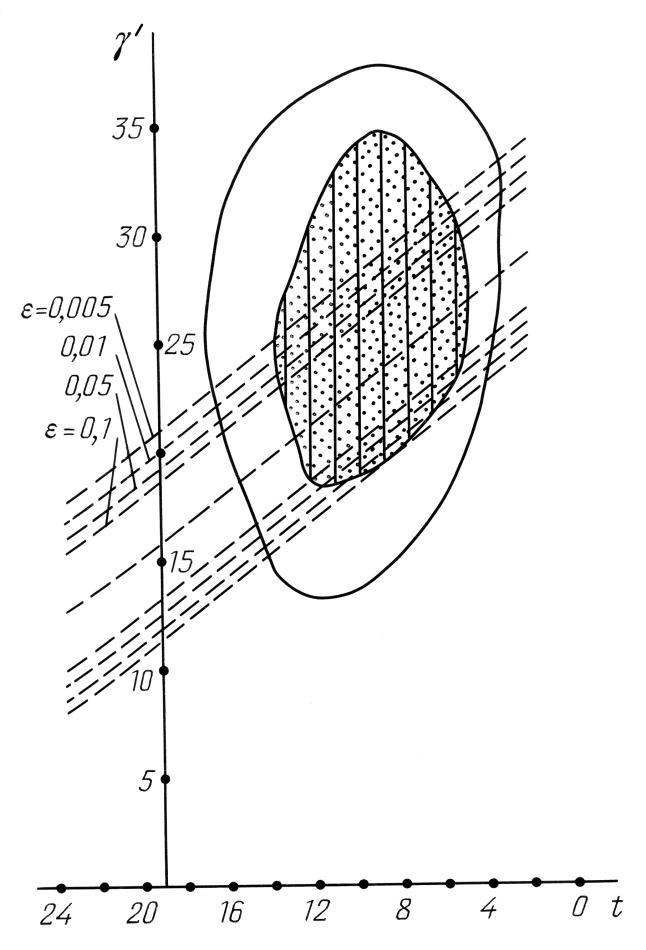
Figura 7.25.
Il risultato della procedura statistica che ha coinvolto
la datazione del catalogo dell'Almagesto tramite
6 delle sue stelle con nome.
Anche la scelta del kernel informativo del catalogo è in buona parte soggettiva. Infatti abbiamo scartato 4 stelle con nome su 12: Canopo, Previndemiatrix, Sirio e Aquila = Altair. Se il rifiuto delle prime due stelle fosse spiegato da ragioni di natura estranea a quelle di cui si occupa il nostro studio, Sirio e Aquila sarebbero state scartate perché gli errori di gruppo delle loro rispettive zone circostanti non coincidono con l'errore di gruppo di Zod A. Tuttavia, nel Capitolo 6 abbiamo dimostrato che ci sono almeno altre due stelle, vale a dire Lira e Capella, per le quali gli errori di gruppo delle zone che le circondano non corrispondono all'errore di gruppo di Zod A. La presunzione precedente è piuttosto di natura arbitraria, poiché non possiamo determinare questi errori. A parte ciò, queste due stelle si trovano a una distanza considerevole dallo Zodiaco e sono vicine a M, una regione misurata relativamente male.
Riflettiamo ora su come sarebbe il possibile intervallo di datazione del catalogo dell'Almagesto se escludessimo queste due stelle, lasciandone solo sei nel kernel informativo del catalogo, ovvero Arturo, Regolo, Antares, Spiga, Aselli e Procione. Possiamo vedere il risultato nella Figura 7.25 (simile alla Figura 7.11). Sebbene il valore dell'area del parametro γ (per il quale la discrepanza latitudinale massima non supera il livello di 10' o 15') è cresciuto sostanzialmente, i confini del possibile intervallo di datazione sono cambiati solo marginalmente. Il limite superiore rimane lo stesso per entrambi i livelli; il limite inferiore per il livello dei 15 minuti rimane lo stesso rispetto a quello che otterremmo se considerassimo le otto stelle del kernel. Il limite inferiore di α = 10' si è spostato indietro nel tempo solo di 100 anni.
Pertanto, se dovessimo prendere in considerazione solo le 6 stelle con nome della regione Zod A o delle aree circostanti, giungeremmo alla conclusione che il catalogo stellare dell'Almagesto potrebbe essere stato compilato non prima del 500 d.C.
6.4. L’esclusione di Arturo non influenza sostanzialmente la datazione del catalogo dell’Almagesto.
Ci troviamo di fronte a un'altra domanda. L'intervallo di datazione del catalogo dell'Almagesto che abbiamo calcolato potrebbe essere il risultato di una sola stella in movimento? Questa domanda ha un senso, dal momento che se dovessimo trovarla il possibile errore nella misurazione delle sue coordinate potrebbe distorcere la risultante datazione. L’unica candidata per quel ruolo di “stella per la datazione” del kernel informativo è Arturo. È la più veloce di tutte e otto le stelle e definisce in buona misura il nostro intervallo di datazione. Le stelle che la circondano non sono state misurate molto bene, vedere il Capitolo 6. Pertanto, se il singolo errore delle coordinate per Arturo fosse abbastanza grande, il possibile intervallo di datazione potrebbe diventare piuttosto distorto.
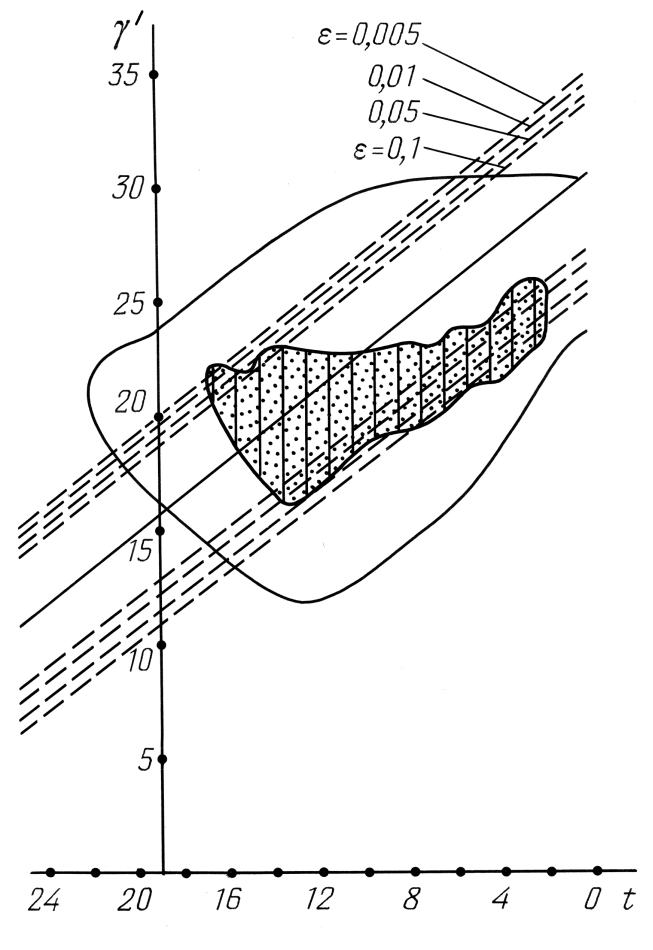
Figura 7.26.
Il risultato della procedura statistica che ha coinvolto
la datazione del catalogo dell'Almagesto
tramite 7 delle sue stelle con nome.
Controlliamo come sarebbe questo intervallo se escludessimo Arturo dal kernel informativo del catalogo dell'Almagesto, limitandolo così a solo sette stelle. La lunghezza del nuovo intervallo naturalmente si estenderà, poiché è sostanzialmente inversamente proporzionale alla massima velocità stellare del kernel informativo del catalogo. Potere vedere il risultato nel diagramma della Figura 7.26, in cui si dimostra chiaramente che anche con l'assenza della stella più veloce del kernel informativo (Arturo), l'area dei 10' non va più indietro nel tempo del 300 d.C. (t = 16), nel livello di confidenza di 1 - ε = 0,95, o inferiore. E' solo quando estendiamo la striscia della confidenza a 1 - ε = 0,99, ossia il 99%, che quest'area inizia a coprire il 200 d.C. Vale a dire che l'epoca scaligeriana di Tolomeo non è inclusa nell'intervallo di datazione, per non parlare dell'epoca ancora più antica di Ipparco.
Consideriamo ora l'area dei 15 minuti. Raggiunge il 100 a.C. (t = 20) nel livello di confidenza 1 - ε = 0,95. Il livello di confidenza 1 - ε = 0,99 consente di raggiungere il 200 a.C., perciò l'epoca scaligeriana di Tolomeo viene raggiunta solo se rallentassimo di molto le condizioni.
Potremmo chiederci se nel nostro caso il livello di confidenza di 1 - ε =0,95 sia sufficiente. A quanto pare è così, dal momento che la precisione definita dal livello del 95% è sufficientemente alta per la ricerca storica; in realtà, quei valori sono considerati accettabili anche per le applicazioni tecniche e quelle che richiedono davvero un livello di precisione molto elevato. Come riferimento citiamo [273], un'opera che si occupa della datazione dell'Almagesto. Per cui abbiamo scelto il valore di ε = 0,2 ottenendo un intervallo di confidenza solo dell'80%. Quindi, le nostre conclusioni hanno un livello molto alto di affidabilità.
Possiamo concludere dicendo che né il cambiamento del livello di confidenza, né le alterazioni nel contingente del kernel informativo, né la variazione del valore di precisione garantito delle misurazioni, possono influire sulla conclusione principale che abbiamo fatto, vale a dire che il catalogo dell'Almagesto è stato compilato molto più tardi del I-II secolo d.C., che è l'epoca scaligeriana di Tolomeo.
7. La datazione geometrica dell’Almagesto.
Le conclusioni a cui siamo arrivati nei paragrafi 2-6 sono state tutte di carattere statistico. I valori effettivi dell'errore di gruppo sono stati determinati con alcuni errori statistici. Pertanto, le conclusioni relative alla coincidenza degli errori di gruppo per le varie costellazioni dell'Almagesto possono essere false, sebbene questa probabilità sia davvero molto bassa, poiché nella sezione precedente abbiamo analizzato la stabilità del nostro risultato statistico. Tuttavia, al fine di garantire l'assenza di errori statistici, mettiamo da parte per un po' la statistica e passiamo a fare solo delle considerazioni geometriche.
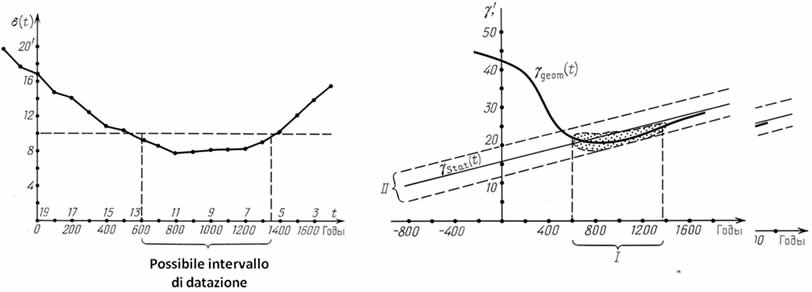
La procedura geometrica di datazione del catalogo
dell'Almagesto: δ(t) = Δb(t, γgeom(t), φ(t)).
Figura 7.28.
Il grafico di dipendenza γgeom(t) insieme all'intervallo di confidenza.
Consideriamo il “minimax della discrepanza latitudinale” per il kernel informativo precedentemente definito nel catalogo dell'Almagesto e che è formato da 8 stelle con nome:
δ(t) = min Δ(t, γ, φ), (7.7.1)
dove il minimo viene selezionato in base a diversi valori di γ e φ, quindi confrontiamo questa equazione con la 7.3.1. L'unica differenza tra le due è il campo alterato dei valori del parametro γ. Nella formula 7.3.1, γ cambia nell'ambito della striscia di confidenza che copre il punto γstat(t). L'equazione 7.7.1 non contiene questa limitazione; pertanto, δ(t) ≤ Δ(t).
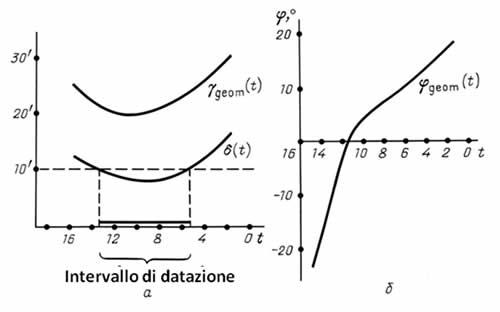
Figura 7.29.
La procedura geometrica di datazione del catalogo dell'Almagesto.
Usiamo γgeom(t) e φgeom(t) per rappresentare i valori di γ e φ che comprendono il minimo della parte destra (7.7.1). La possibile bassa precisione di γgeom(t) e la procedura di stima φgeom(t) qui sono di scarsa importanza.
Ricordiamo la situazione che abbiamo già incontrato nel paragrafo 3, in cui sono state rimosse le limitazioni dal parametro φ. Queste limitazioni riguardavano solo γ. Come abbiamo visto, conduce a un intervallo di datazione che rimane inalterato per mezzo delle caratteristiche di stima statistica di φ. Ciò nonostante, l'intervallo è ampio. Faremo qualcosa del genere con entrambi i parametri (γ, φ). I valori di γstat(t) e φgeom(t) che abbiamo introdotto possono essere considerati come i parametri per definire l'errore di gruppo del kernel informativo del catalogo, purché questo sia stato compilato in una certa epoca t.
Tenendo conto di tutto quanto detto in precedenza, consideriamo che il possibile intervallo di datazione del catalogo sia in tutti questi momenti di t presi nel loro insieme, per cui δ(t) ≤ 10'. Per trovare questo intervallo, disegniamo il grafico di δ(t) nelle Figure 7.27, 7.28, 7.29 e 7.30, come anche i grafici delle funzioni γgeom(t) e φgeom(t). Il grafico risultante di δ(t) è stato costruito secondo la formula 7.7.1, mentre i valori di Δ(t, γ, φ) sono stati calcolati dalla 7.3.1 con la successiva risoluzione di γ e φ. Per confronto, possiamo studiare il grafico di dipendenza φgeom(t) nella Figura 7.28 completo della striscia di confidenza (vedere il paragrafo 6). Si può anche vedere che l'area dei valori di (t, γ) per i quali Δ(t, γ, φ) <10' con un certo valore di φ.
Secondo questi grafici, l'intervallo di datazione del catalogo dell'Almagesto precedentemente stimato non si espande nemmeno se usassimo una procedura di datazione geometrica. Questa è un'ulteriore prova del fatto che le nostre stime statistiche di γstatZod A calcolate per la maggioranza delle stelle del catalogo dell'Almagesto corrispondono di fatto all'errore di gruppo nella piccola serie di stelle con nome dell'Almagesto. A parte ciò, abbiamo dimostrato che non esiste alcuna opzione per associare l'effettiva sfera celeste con le stelle dell'Almagesto, in modo tale che tutte le stelle abbiano una discrepanza latitudinale inferiore a 10' in qualsiasi punto al di fuori dell'intervallo tra il 600 d.C. e il 1300 d.C.
Concludiamo riportando i grafici di dipendenza della presunta datazione t per le singole discrepanze latitudinali di tutte e 8 le stelle del kernel informativo dell'Almagesto nei valori fissi di γ = 20' e φ = 0 (vedere la Figura 7.31). La parte superiore di questi grafici è simile alla curva della Figura 7.25 che rappresentala la dipendenza della discrepanza minima della presunta datazione t per la maggior parte dell'intervallo temporale dopo lo 0 d.C. (0 < t <9). Ciò risulta dal v alore di γ = 20', che è vicino a quello di γgeom(t), mentre φ = 0 è vicino a φgeom(t) per la maggior parte di questo intervallo. Il risultato non è particolarmente sensibile alla variazione del valore di φ.
La Figura 7.31 mostra esattamente quali sono le stelle del kernel informativo del catalogo dell'Almagesto che consentono di raggiungere il valore minimo della discrepanza latitudinale δ(t) per le diverse datazioni presunte t. Nella Figura 7.31 si può vedere chiaramente la concentrazione dei valori della discrepanza latitudinale pari a zero, vicini a t = 10, ossia il 900 d.C. circa. Questa datazione presunta del catalogo praticamente sradica simultaneamente le discrepanze per tre stelle del kernel informativo, vale a dire Arturo (α Boo), Regolo (α Leo) e Procione (α CMi). Per tutte le altre stelle del kernel informativo, è solo la discrepanza latitudinale di Aselli (γ Can) che raggiunge lo zero vicino all'inizio della nuova era.
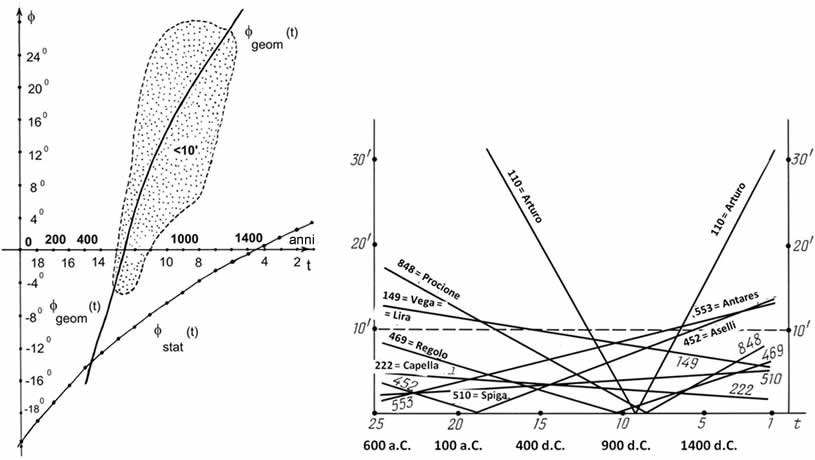
Figura 7.30. La procedura geometrica di
datazione del catalogo dell'Almagesto.
Figura 7.31.
Le discrepanze latitudinali individuali del catalogo dell’Almagesto con β ≈ 0’ ≈ 21’.
Sarebbe interessante esaminare il possibile collegamento tra la suddetta concentrazione di discrepanze pari a zero e il fatto che Arturo e Regolo, come pure Sirio, occupavano un ruolo estremamente importante nell'astronomia “antica”. Arturo, ad esempio, deve essere stata la prima stella ad aver ricevuto un nome proprio nell'astronomia greca “antica”, in quanto è la stella più luminosa dell'emisfero boreale. È stata menzionata in un poema “antico” di Arato che contiene riferimenti alla sfera celeste. Regolo è la stella che nell'astronomia greca viene utilizzata come riferimento per la misurazione delle coordinate di tutte le altre stelle e dei pianeti.