CAPITOLO 10
di A. T. Fomenko e G. V. Nosovskiy.
Considerazioni aggiuntive riguardo la datazione dell’Almagesto. Gli oscuramenti stellari e le eclissi lunari.
1. Introduzione.
Il libro di A. T. Fomenko V. V. Kalashnikov e G. V. Nosovskiy intitolato La Datazione del Catalogo Stellare dell'Almagesto. Analisi Statistica e Geometrica ([Metodi 3]: 2) parla dello studio sulla questione della copertura delle stelle da parte dei pianeti descritta nell'Almagesto. Tra l'altro, il presente capitolo contiene degli ulteriori calcoli più precisi che abbiamo fatto successivamente in questo campo.
La datazione del catalogo stellare dell'Almagesto a cui siamo giunti nei capitoli precedenti, basando la nostra ricerca sull'analisi geometrica e statistica delle latitudini stellari, ovviamente contraddice piuttosto drasticamente la datazione consensuale riguardo la compilazione dell'Almagesto (il presunto 137 d.C.). Questo ci porta alla domanda se il catalogo stellare dell'Almagesto possa essere un addendum più recente, realizzato per un testo antico autentico. Oppure potrebbe essere vero il contrario, vale a dire che l'intero testo dell'Almagesto fu scritto agli inizi del 600 d.C. e infine modificato durante l'epoca tardo medievale (dalla fine del XVI secolo all'inizio del XVII secolo).
Abbiamo già detto che le osservazioni astronomiche raccolte nell'Almagesto sono state studiate meticolosamente e professionalmente da Robert Newton, un famoso scienziato americano specializzato in meccanica celeste, navigazione e astrofisica (vedere [614]). Il risultato della sua ricerca può essere formulato brevemente come segue: secondo Newton, quei dati dell'osservazione astronomica contenuti nell'Almagesto che possono essere calcolati con l'aiuto della teoria di Tolomeo descritta nell'Almagesto (compresa la teoria del moto solare, lunare e planetario, come pure i dati della precessione), non sono altro che i risultati dei successivi calcoli teorici effettuati dallo stesso Tolomeo o da qualcun altro che ha agito per conto di Tolomeo). Ai nostri giorni è quindi inutile utilizzare questi “dati calcolati” per ottenere delle datazioni astronomiche indipendenti, poiché la datazione di queste “osservazioni calcolate” implica essere dell'opinione che esista un autore successivo, uno che visse nel XV-XVII secolo, nel periodo in cui furono eseguite queste osservazioni astronomiche.
Fortunatamente, ci sono dei dati relativi alle osservazioni anche nell'Almagesto e questi non possono essere stati calcolati o contraffatti tramite la teoria di Tolomeo o qualsiasi altra teoria astronomica del Medioevo. Tra questi dati possiamo sicuramente contare le latitudini dell'eclittica delle 1020 stelle contenute nel catalogo dell'Almagesto. Formano un volume considerevole di informazioni che abbiamo usato per datare con successo l'Almagesto, vedere i precedenti capitoli del libro.
L'Almagesto contiene anche alcuni altri dati astronomici che i commentatori moderni considerano essere il risultato di osservazioni “antiche”, vale a dire:
- Le quattro “antiche” osservazioni delle stelle oscurate dal moto dei pianeti.
- Le circa venti (ossia 21) “antiche” eclissi lunari menzionate nell'Almagesto.
Facciamo notare che gli astronomi tardo medioevali del XVI-XVII secolo potrebbe aver tentato di calcolare gli “antichi oscuramenti delle stelle da parte dei pianeti” usando la teoria di Tolomeo e i periodi della rotazione planetaria attorno al sole. Questi periodi erano già ben noti nel XVI-XVII secolo; tale conoscenza è sufficiente per il calcolo della corrispondenza longitudinale tra la stella e il pianeta. L'esatto oscuramento, ovvero la corrispondenza di entrambe le coordinate, andava ovviamente ben oltre la loro capacità di calcolo. Non si deve escludere la possibilità di trovare dei risultati di calcolo imprecisi degli astronomi medievali, presentati in seguito come “antiche osservazioni astronomiche”.
Lo stesso vale ancor di più per le eclissi lunari. La teoria del moto lunare sviluppata dagli astronomi del XV-XVII secolo diede vita a molti calcoli approssimativi riguardo le date e le fasi delle eclissi lunari passate e future, verosimili nel XVII secolo. Pertanto le “antiche” eclissi lunari descritte nell'Almagesto avrebbero potuto essere state facilmente calcolate nel XVI-XVII secolo. L'inevitabile mancanza di precisione manifestata nei calcoli medievali delle fasi, potrebbe essere stata dichiarata a seguito degli “errori commessi dall'antico osservatore” che stimò le fasi dell'eclissi ad occhio nudo, e quindi approssimativamente. In questo modo, le eclissi lunari sono meno istruttive rispetto agli oscuramenti, dal momento che a differenza delle fasi dell'eclissi, l'oscuramento può essere osservato ad occhio nudo. I falsificatori del XVI-XVII secolo erano già abbastanza in grado di includere nell'Almagesto le eclissi lunari calcolate come prova dell'origine antica del testo.
C'è un altro fatto notevole che merita di essere menzionato nel presente capitolo. Come discuteremo più dettagliatamente in seguito, l'Almagesto non contiene alcuna “antica” eclissi solare. Perché mai? Dopo tutto, le eclissi solari sono di gran lunga più straordinarie di quelle lunari. Si potrebbe benissimo considerarle come i candidati principali da includere nell'Almagesto. Riteniamo che la risposta sia abbastanza semplice. Sembra proprio che nella sua forma attuale l'Almagesto abbia subito molte falsificazioni nel XVI-XVII secolo, volte a farlo diventare un libro molto più antico. Pertanto, l'Almagesto contiene una sostanziale quantità di calcoli medievali inversi e teorici. La teoria dell'eclissi solare è più complessa di quella dell'eclissi lunare, per cui i calcoli delle eclissi solari sarebbero stati un compito formidabile per gli astronomi di fine XVI inizio XVII secolo. Questa è la ragione apparente del perché furono abbastanza cauti da astenersi dall'includere le segnalazioni delle “antiche” eclissi solari nel “antico” Almagesto: furono consapevoli del fatto che le generazioni successive di astronomi avrebbero scoperto facilmente la frode.
Di seguito prenderemo in considerazione nei dettagli il problema della datazione degli oscuramenti planetari delle stelle per mezzo delle loro descrizioni trovate nell'Almagesto. E' venuto fuori che questo problema non ha una soluzione astronomica esatta: le uniche soluzioni che abbiamo trovato sono di natura approssimativa. La migliore a cui siamo arrivati è medievale e concorda bene con la datazione del catalogo stellare dell'Almagesto riportata in precedenza. Tuttavia, dobbiamo ribadire che non possono essere utili per la datazione dell'Almagesto, a prescindere dal fatto che siano approssimative. Non si può ancora ignorare il fatto che sono entrambi delle soluzioni medievali che corrispondono bene al nostro risultato principale: la datazione medievale del catalogo stellare dell'Almagesto e l'epoca relativamente recente della sua edizione finale nel XVI-XVII secolo.
Alla fine del presente capitolo, nel paragrafo 8 prenderemo in considerazione la possibilità di datare l'Almagesto attraverso le descrizioni delle eclissi lunari.
2. La datazione degli oscuramenti planetari delle stelle. I calcoli coinvolgono gli elementi medi.
È risaputo che l'Almagesto descrive solo quattro oscuramenti stellari da parte dei pianeti (per esempio, vedere [614]).
Il testo di Tolomeo dice quanto segue:
- Capitolo X.4: “Tra le antiche osservazioni ne abbiamo scelta una, descritta da Timocharis nel modo seguente: nel 13° anno di Filadelfo, il 17-18 del Mesore egizio, nella 12° ora Venere oscurò completamente la stella situata di fronte a Vindemiatrix” ([1355], pagina 319). Tolomeo (nella traduzione di C. Tagliaferro) procede nel dirci che “l’osservazione fu condotta nell’anno 406 dopo Nabonassar” ([1355], pagina 319). Tuttavia, la traduzione di I. N. Veselovskiy ci dice che “l’anno dell’osservazione era il 476 dopo Nabonassar” ([704], pagina 322). Questa circostanza è stata segnalata da M. E. Polyakov. Tagliaferro potrebbe essersi sbagliato, dal momento che Tolomeo continua citando un calcolo in cui si dimostra che sono trascorsi 408 anni da questo oscuramento e l’anno 884 da Nabonassar ([1355], pagina 319). L’oscuramento ha quindi avuto luogo nell’anno 476 da Nabonassar, che d’ora in poi sarà la nostra versione principale. D’altra parte, è anche possibile che C. Tagliaferro stesse usando altre versioni dell’Almagesto in cui viene esplicitamente riportato il 406 dopo Nabonassar. Ciò potrebbe derivare dalle discrepanze inerenti alle diverse copie dell’Almagesto, per cui dovremmo considerare formalmente anche questa versione, che per noi sarà la “versione errata”.
- Capitolo X.9: “Abbiamo considerato una delle vecchie osservazioni, quella che chiarisce che nel 13° anno di Dionigi, nella mattina del 25 di Aigon, Marte oscurò la stella più a nord sulla fronte dello Scorpione” ([1355]), pagina 342. Tolomeo (nella traduzione di C. Tagliaferro) ci dice che “le osservazioni risalgono al 42° anno dopo la morte di Alessandro [ovvero l'anno 476 da Nabonassar]" ([1355], pagina 342). D'altro canto, la traduzione fatta da I. N. Veselovskiy afferma che “il periodo di questa osservazione corrisponde all'anno 52 dopo la morte di Alessandro, ossia il 476 da Nabonassar” ([704], pagine 336-337). O Tagliaferro ha commesso un altro errore di stampa, o la cronologia di Tolomeo nasconde delle distorsioni. Non sarebbe così sorprendente, poiché Tolomeo usa diverse epoche e continua a convertire le datazioni tra loro, cosa che ovviamente può generare degli errori. Ad ogni modo, entrambe le traduzioni ([1355] e [704]) citano lo stesso anno per l'oscuramento stellare di Marte, vale a dire il 476.
- Capitolo XI.3: “Abbiamo di nuovo considerato una vecchia osservazione molto accurata, che ci dice che nel 45° anno di Dionigi, nel 10° del Partenone Giove oscurò l'Asse del Nord” ([1355], pagina 361). Inoltre, secondo entrambe le traduzioni (Tagliaferro e Veselovskiy), “questa volta corrisponde al 83° anno dalla morte di Alessandro” ([1355], pagina 361; anche [704], pagine 349-350). In questo caso non c'è discrepanza tra le due diverse traduzioni dell'Almagesto.
- Capitolo XI.7: “Abbiamo preso in considerazione un'altra vecchia osservazione accurata, secondo la quale il 5 di Xanticus dell'anno caldeo 82, Saturno era situato due unità sotto la spalla sud della Vergine” ([1355], pagina 379). Più avanti, entrambe le traduzioni (Tagliaferro e Veselovskiy) ci informano che “il tempo in questione corrisponde all'anno 519 dopo Nabonassar” ([1355],pagina 379; anche [704], pagina 362). Anche in questo caso non c'è discrepanza tra le due diverse traduzioni dell'Almagesto.
Secondo le identificazioni tradizionali conosciute delle stelle tolemaiche con le loro controparti moderne (vedere [614] e [1339]), gli oscuramenti in questione possono essere i seguenti:
- Venere oscurò η Vir intorno alle 12.
- Marte oscurò β Sco al mattino.
- Giove oscurò δ Can all'alba.
- Alla sera Saturno fu osservato “due unità” più in basso di γ Vir.
Abbiamo verificato queste identificazioni e si sono dimostrate corrette. Come riferimento per i calcoli, il libro di A. T. Fomenko, V. V. Kalashnikov e G. V. Nosovskiy ([Metodi 3]: 2) usa i valori degli elementi medi delle orbite planetarie presi dal libro d G. N. Duboshin ([262]); la precisione latitudinale è pari più o meno a 1". Siccome abbiamo preso in considerazione il problema della precisione del calcolo, ci piacerebbe chiarire cosa intendiamo dire esattamente con “il pianeta ha oscurato una stella”.
È risaputo che l'occhio umano può distinguere due punti situati a una distanza angolare di 1'. Per le persone con una vista particolarmente acuta, questa distanza può essere pari a 30". La questione è che la dimensione caratteristica dei coni retinici al centro del fondo oculare corrisponde a 24". Pertanto, l'oscuramento di una stella da parte di un pianeta o loro reciproca sovrapposizione, in realtà significa che la distanza angolare tra loro equivale circa a 1' visto dalla Terra.
La teoria moderna consente di calcolare le posizioni passate di Venere e Marte con una precisione latitudinale di 1' per l'intervallo storico che ci interessa. La precisione nel calcolo delle latitudini di Marte e Venere in movimento è uguale a circa 3". E' sufficiente, poiché si tratta del valore latitudinale che di fatto definisce che una stella è stata coperta da un pianeta. La longitudine di un pianeta si altera piuttosto rapidamente rispetto alla sua latitudine. A livello locale, la longitudine può essere considerata proporzionale al tempo. Per cui, un errore di diversi gradi d'arco nella stima della longitudine, porta solo a un errore molto piccolo nella stima del momento in cui il pianeta ha oscurato la stella. Pertanto, nel caso di Venere e Marte gli oscuramenti descritti da Tolomeo possono essere calcolati con sufficiente precisione, una volta che si usa come base la teoria moderna.
La teoria del moto di Giove e Saturno è più complessa e un po' meno precisa di quella utilizzata per Venere e Marte. V. K. Abalakin ha ragione a sottolineare che “nella misura in cui vengono interessati i pianeti esterni (Giove, Saturno, Urano, Nettuno e Plutone) ... gli elementi orbitali centrali [di questi pianeti] non possono in alcun modo essere utilizzati per la soluzione del problema della stabilità e rimangono applicabili per intervalli di diversi milioni di anni ... sono solo utili per un periodo di diversi secoli prima e dopo l'epoca attuale” ([1], pagina 302).
Tuttavia, nel caso dell'Almagesto non abbiamo la necessità di avere delle formule ultra precise. Il motivo è che, secondo l'Almagesto, l'osservazione di Saturno è di secondaria importanza, poiché il pianeta non ha coperto la stella, ma piuttosto è stato osservato a una distanza di “due unità” da essa; per quanto riguarda l'effettiva definizione tolemaica di “unità”, il problema rimane poco chiaro. Pertanto, il calcolo delle posizioni di Saturno con la precisione di 1' non ci è di alcuna utilità.
Per quanto riguarda Giove, Tolomeo afferma che possa aver “oscurato una stella”; tuttavia, i moderni calcoli teorici dimostrano che Giove non si è avvicinato a δ Cancer più di 15' da qualsiasi punto dell'intervallo storico; pertanto, dobbiamo cercare i momenti dove la distanza tra Giove e la stella in questione erano pari a 15' - 20'. Per questo scopo non è necessaria la precisione estrema delle formule; il livello garantito dalla teoria moderna è più che sufficiente.
Ora affrontiamo il problema di come sono stati datati questi quattro oscuramenti da Tolomeo (vedere la Tabella 10.1). L'era principale usata da Tolomeo è l'era di Nabonassar ([1355]). È più incline a usarla per ricalcolare le datazioni delle antiche osservazioni. Usa anche altre epoche cronologiche. Riportiamo la tabella delle datazioni contenente i suddetti oscuramenti stellari da parte dei pianeti, citati da Tolomeo. L'astronomo usò almeno due volte ciascuna delle seguenti tre epoche: l'era di Nabonassar, l'era di Alessandro e l'era di Dionisio.
Siamo giunti con i seguenti intervalli tra gli oscuramenti:
- Un massimo di un anno tra gli oscuramenti di Venere e Marte (476 e 476). Se la “versione errata” in realtà non contenesse affatto degli errori, l'intervallo sarebbe pari a 70 anni: 476 - 406 = 70.
- 32 anni dall'era di Dioniso tra gli oscuramenti di Marte e Giove (45 - 13 = 32); in alternativa, circa 31 anni dall'era di Alessandro (83 - 52 = 31).
- Circa 11 anni tra gli oscuramenti di Giove e Saturno (519 - 508 = 11).
| Tabella 10.1. Le datazioni degli oscuramenti stellari da parte dei pianeti come indicate nell'Almagesto. |
|||
| L’oscuramento della stella da parte del pianeta | Anni secondo Tolomeo | ||
| Era di Nabonassar | Era di Alessandro | Era di Dioniso | |
| 1) Venere | 476 o 406 (il 406 è un errore di stampa?) |
||
| 2) Marte | 476 | 52 o 42 (42 è un errore di stampa?) |
13 |
| 3) Giove | 83 | 45 | |
| 4) Saturno | 519 | ||
Se le suddette discrepanze tra le traduzioni dell'Almagesto fatte da C. Tagliaferro e I. N. Veselovskiy non fossero il risultato di errori di stampa, ma piuttosto derivassero da effettive discrepanze tra i vari manoscritti dell'Almagesto (di cui ce ne erano molti, vedere il Capitolo 11), la Tabella 10.1 dimostrerebbe che la cronologia tolemaica potrebbe contenere degli errori. L'altra possibilità, e anche quella più interessante, è la presenza di errori anche nelle edizioni moderne dell'Almagesto, meticolosamente verificate dagli scienziati. Il fatto che la cronologia di Tolomeo non fosse priva di errori viene dimostrato dalla sopra citata Tabella 10.1. Infatti, l'intervallo tra gli oscuramenti di Marte e Giove equivale a 32 anni dall'era di Dioniso (45 - 13 = 32). Se volessimo prendere l'era di Alessandro, questo l'intervallo sarebbe pari a 31 anni (83 - 52 = 31). La discrepanza equivale a un anno.
Secondo Tolomeo, la stella in questione è stata oscurata da Giove nell'anno 508 dopo Nabonassar. Questo è palesemente implicito nella Tabella 10.1.
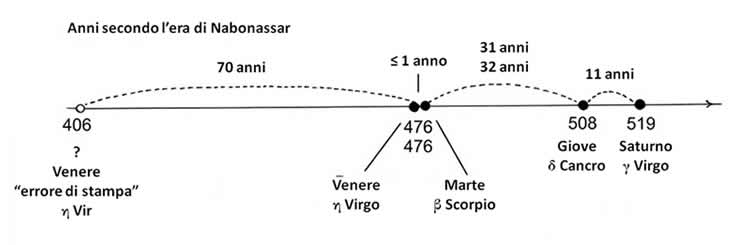
Figura 10.1.
Le quattro osservazioni dei pianeti che oscurano le stelle menzionate nell'Almagesto.
Le datazioni sono state fornite in base all'era di Nabonassar usata da Tolomeo.
Formuliamo un preciso problema matematico, vedere la Figura 10.1. Dobbiamo determinare le seguenti combinazioni di eventi astronomici:
- In un certo anno N, ovvero l'anno N - 70, Venere oscurò η Virgo verso le 12.
- Nell'anno N Marte oscurò β Scorpio nella mattina.
- Nell'anno N + 32 (o N + 31) Giove oscurò δ Cancer all'alba.
- Nell'anno N + 43, di sera Saturno era situato vicino a γ Virgo ed era leggermente più in
Parliamo ora del problema riguardo la precisione e la velocità necessarie per soddisfare gli intervalli di tempo tra gli oscuramenti planetari delle stelle sopra elencati. E' ovvio che abbiamo bisogno di un margine di almeno due anni, poiché tutte le date sono state rese in una sola era, cosa che può produrre un errore naturale di 1-2 anni nel calcolo formale, semplicemente a causa del fatto che le diverse epoche hanno usato dei punti diversi per segnare l'inizio dell'anno (è risaputo che tali punti includevano marzo, agosto, settembre, ottobre e gennaio). L'inizio variabile dell'anno è stato usato anche in ([1155]). Siamo d'accordo sulla discrepanza accettabile dell'intervallo di 4 anni, il che significa che l'intervallo di tempo trovato non può differire da quello tolemaico per più di 4 anni.
Di conseguenza, dobbiamo trovare quattro oscuramenti con i seguenti intervalli tra loro:
- Un anno al massimo tra gli oscuramenti di Venere e Marte, con un tasso di aberrazione di 4 anni. Se la “versione errata” in realtà non contenesse errori di stampa, l'intervallo dovrebbe coprire 70 anni con un tasso massimo di aberrazione pari a 4 anni.
- 31 o 32 anni tra gli oscuramenti di Marte e Giove con un tasso di aberrazione di 4 anni.
- 11 anni tra gli oscuramenti di Giove e Saturno con un tasso di aberrazione di 4 anni.
E così abbiamo formulato un preciso problema matematico. Procediamo a formulare la soluzione a cui siamo giunti, che è il risultato dei calcoli degli elementi medi.
Ci sono solo tre soluzioni per il problema matematico formulato sull'intervallo storico tra il 500 a.C. e il 1700 d.C. Queste soluzioni sono approssimative e quindi non precise.
La prima soluzione (medievale, X-XI secolo). Questa soluzione è stata ottenuta da A. T. Fomenko, V. V. Kalashnikov e G. V. Nosovskiy, ed è stata descritta in [Metodi 3]: 2.
1a) Il 18 ottobre 960 d.C., Venere oscurò η Virgo. In questo caso la distanza calcolata è pari a 1' - 2'.
1b) Nella “versione errata” (vedi sopra) questo oscuramento ebbe luogo il 9 settembre 887 d.C. La distanza calcolata tra loro è inferiore a 1'. Tuttavia, in questo caso le condizioni di osservazione erano piuttosto povere.
1c) La “versione errata” consente un'altra soluzione, vale a dire che l'oscuramento di Venere in questione potrebbe aver avuto luogo un anno dopo, il 21 ottobre 888 d.C. In questo caso la distanza calcolata tra loro è meno di 5'.
2) Il 14 febbraio 959 d.C. Marte oscurò β Scorpio. La distanza calcolata tra loro è pari a 15'.
3) Il 25 luglio 994 d.C. Giove era a una distanza approssimativa di 15' da δ Cancer. A proposito, questa distanza è vicina alla distanza minima possibile tra la stella e il pianeta in questione sull'intero intervallo storico in studio.
4) Il 16 agosto 1009 d.C. Saturno si trovava a una distanza di 25' - 30' da γ Virgo, sotto la stella.
Qualora volessimo misurare tutte le distanze tolemaiche in anni, il massimo “intervallo di tolleranza” negli intervalli tra le osservazioni successive sarebbe pari a 4 anni per la prima soluzione. Infatti:
- L'intervallo tra gli oscuramenti di Venere e Marte corrisponde a un anno, cioè il 960 d.C. per Venere e il 959 d.C. per Marte. La distanza massima necessaria è di un anno ± 4 anni.
- L'intervallo tra gli oscuramenti di Marte e Giove corrisponde a 35 anni: il 959 d.C. per Marte e il 994 d.C. per Giove. Abbiamo bisogno di 31 o 32 ± 4 anni.
- L'intervallo tra gli oscuramenti di Giove e Saturno equivale a 15 anni: il 994 d.C. per Giove e il 1009 d.C. per Saturno. Abbiamo bisogno di 11 ± 4 anni.
La seconda soluzione (“tradizionale”, III secolo a. C.). È stata descritta, per esempio, nel libro di Robert Newton ([614], pagina 335).
- La notte del 11-12 ottobre 272 a.C. (o l'anno 271) vide Venere avvicinarsi a η Virgo. La distanza tra Venere e la stella in questione è pari a circa 1' - 3'.
- La mattina del 16 o 18 o gennaio del 272 a.C. (o l'anno 271) Marte “si avvicinò” a β Scorpio. Tuttavia, secondo Y. A. Grebenikov, l'editore scientifico dell'edizione russa del libro di R. Newton, nel mattino del 18 gennaio “al momento dell'osservazione Marte era a una distanza di circa 50' da β Scorpio, [ARO, sezione XI.4] e questa distanza difficilmente può essere considerata nelle immediate vicinanze. Tuttavia, Marte e la stella in questione erano molto vicine tra loro il 16 gennaio 271, per cui la data potrebbe essere stata scritta erroneamente o essere stata male interpretata da Tolomeo” ([614], pagina 312, commento 3). Secondo i nostri calcoli, il 18 gennaio 272 a.C., la distanza tra Marte e la stella fu pari a circa 50' -55', mentre il giorno 16 fu maggiore di 15' (più precisamente, 17' - 18'); questa soluzione è quindi dubbia.
- La mattina del 4 settembre 241 a.C., Giove “si avvicinò” a δ Cancer. Tuttavia, i calcoli dimostrano che la distanza tra Giove e la stella in questione era più grande di 25'.
- Il 1 marzo 229 a.C. Saturno era a una distanza di circa 30' da γ Virgo.
Tutte le datazioni sono state fornite secondo il calendario giuliano, con l'inizio dell'anno che cade il 1° di gennaio.
Nella soluzione “antica” gli intervalli tra gli oscuramenti sono i seguenti: gli oscuramenti di Marte e Venere ebbero luogo lo stesso anno, gli oscuramenti di Marte e Giove erano separati da un intervallo di 31 anni, mentre gli oscuramenti di Giove e Saturno si trovavano a una distanza di 12 anni l'uno dall'altro.
La terza soluzione (tardo medioevo, XV-XVI secolo). Questa soluzione è stata scoperta da A. T. Fomenko e G. V. Nosovskiy.
- Il 19 settembre 1496 d.C., Venere oscurò η Virgo. In questo caso, la distanza calcolata è inferiore di 1'.
- Il 19 gennaio 1497 d.C. Marte oscurò β Scorpio. La distanza calcolata tra loro è di circa 15'.
- Il 3 giugno 1528 d.C. Giove si avvicinò a δ Cancer. La distanza tra loro è pari a circa 25'.
- Il 5 settembre 1539 d.C. Saturno era situato circa 25' sotto γ Virgo.
La soluzione tardo medievale del XV-XVI secolo ha una tolleranza di 1 anno al massimo per le date degli intervalli tolemaici tra le osservazioni consecutive. Dal punto di vista degli intervalli temporali tra gli oscuramenti, questa soluzione è la migliore delle tre: è quella ideale. Infatti:
- L'intervallo tra gli oscuramenti di Venere e Marte equivale a soli quattro mesi (19 settembre 1496 d.C. per Venere e 19 gennaio 1497 d.C. per Marte). In altre parole, meno di un anno; si adatta perfettamente all'intervallo tolemaico richiesto.
- L'intervallo tra gli oscuramenti di Marte e Giove corrisponde a 31 anni: il 1497 d.C. per Marte e il 1528 d.C. per Giove. Secondo Tolomeo ci sono voluti 31 o 32 anni.
- L'intervallo tra gli oscuramenti di Giove e Saturno equivale a 11 anni: il 1528 d.C. per Giove e il 1539 d.C. per Saturno. Questo è il periodo esatto che è passato secondo Tolomeo: undici anni.
Come vedremo di seguito, la soluzione “antica” è visibilmente peggiore delle soluzioni medievali che abbiamo calcolato. I cronologisti che studiarono l'Almagesto non riuscirono a soddisfare le specifiche di Tolomeo. È anche ovvio che i cronologisti non evidenziarono la corrispondenza tra l'osservazione descritta da Tolomeo e i calcoli moderni, o persino le date di queste osservazioni fornite dallo stesso Tolomeo, ma piuttosto l'interpretazione ambigua dei nomi di Tolomeo per i mesi e per quelle caratteristiche astronomiche come la longitudine del sole, il momento di osservazione, la longitudine planetaria ecc... che furono calcolate dall’astronomo mediante l'uso di una teoria piuttosto imprecisa.
In ogni caso, questi dati non possono servire da base per la datazione delle osservazioni effettive. La datazione dovrebbe basarsi sulle caratteristiche di osservazione che Tolomeo cita come opposte ai calcoli, vale a dire l'anno in cui la stella era coperta dal pianeta e il fatto stesso dell'oscuramento.
La soluzione del X-XI secolo è quella che soddisfa al meglio la descrizione di Tolomeo. Facciamo notare che si trova nel mezzo del possibile intervallo di datazione che abbiamo calcolato per il catalogo stellare di Tolomeo. La soluzione tardo medievale del XV-XVI secolo d.C. è anche possibile dal punto di vista della Nuova Cronologia. Difatti, l'antica soluzione è situata a una distanza di 1800 anni da quella tardo medievale, che è il valore di uno degli spostamenti cronologici chiave inerenti alla versione scaligeriana della storia, vedere Cronologia 1. L'esistenza di diverse soluzioni, tra cui quella “antica” del III secolo a.C., è spiegata dall'esistenza di certi periodi nell'oscuramento planetario delle stelle. La configurazione piatta della Terra e dei pianeti che definisce la possibilità di osservare questi oscuramenti dalla Terra (a patto che i piani orbitali planetari siano posizionati entro un angolo soddisfacente dall'eclittica), cambia nel corso del tempo; questi cambiamenti sono conformi a una legge periodica approssimativa. Infatti, la dinamica di questa configurazione può essere descritta come il movimento di un punto lungo le curve del toro multidimensionale. Tuttavia, gli angoli tra i piani orbitali planetari e l'eclittica cambiano gradualmente con il corso del tempo. Abbiamo scoperto che può passare un intero periodo, nel lasso di tempo necessario affinché queste alterazioni “distorcano” la configurazione delle orbite planetarie.
3. La datazione degli oscuramenti planetari delle stelle descritti nell’Almagesto, con un calcolo molto più preciso.
3.1. L’algoritmo modificato.
I nostri calcoli riguardo gli oscuramenti planetari delle stelle citati nel paragrafo precedente, erano basati sulle formule astronomiche prese dal libro di G. N. Duboshin ([262]). Inoltre, mentre A.T. Fomenko, V. V. Kalashnikov e G. V. Nosovskiy stavano conducendo quei calcoli nel 1990, usarono solo gli elementi orbitali medi. Furono stimati con sufficiente precisione nel XIX-XX secolo; tuttavia, se non tenessimo conto delle aggiunte periodiche, finiremmo con avere delle posizioni planetarie piuttosto approssimative. La mancanza di queste aggiunte periodiche nei nostri calcoli degli oscuramenti planetari è chiaramente visibile dalle formule planetarie che abbiamo citato in [Metodi 3]: 2. Questi calcoli sono bastati per gli scopi che stavamo perseguendo a quel tempo. Infatti, le considerazioni puramente geometriche rendono ovvio che la soluzione approssimativa a cui siamo giunti con l'utilizzo degli elementi medi, è abbastanza stabile. Per cui, se “spostassimo un po' le date” potremmo usarla per ottenere una soluzione precisa. A quel tempo non stavamo cercando una soluzione precisa, quindi non siamo andati oltre i calcoli approssimativi (che riflettevano lo stesso abbastanza bene la situazione) per i seguenti motivi.
In primo luogo, i calcoli degli oscuramenti planetari delle stelle sono di secondaria importanza. Sono oltre lo scopo del problema principale, ovvero la datazione dei vecchi cataloghi stellari; possono essere utilizzati solo per definire le direzioni possibili per ulteriori analisi dell'Almagesto, allo scopo di datare le altre parti e non solo il catalogo stellare.
Il secondo motivo per cui a quei tempi non usammo una teoria planetaria più precisa, ma ricorremmo alle formule piuttosto approssimative ma stabili degli elementi medi, è il seguente. Prima degli anni '80 c'erano diverse versioni della teoria del calcolo planetario che davano delle risposte incoerenti per epoche lontane. E' facile da capire il perché. Tutti i tentativi di creare delle formule planetarie più precise si basano in larga misura su differenti correzioni empiriche. Queste correzioni derivano da osservazioni moderne. Ciò implica la loro utilità allo scopo di creare delle formule moderne più precise. Tuttavia, la questione che queste correzioni vadano bene solo per le epoche lontane, è tutt'altro che semplice.
Negli ultimi due anni, i metodi di calcolo usati nella teoria planetaria sono stati migliorati notevolmente. Ci sono stati numerosi gruppi di astronomi che usavano approcci diversi ed escogitavano formule che davano soluzioni molto precise anche per le epoche lontane.
Questo è ben lungi dall'essere la prova assoluta della validità di tali teorie applicate alle epoche in questione, ma è abbastanza valida. In linea generale, la situazione attuale dei calcoli per la teoria planetaria differisce da quella riflessa nel libro di G. N. Duboshin ([262]) del 1976.
Pertanto, ai giorni nostri ha senso tornare al problema di datare gli oscuramenti planetari delle stelle con l'uso di formule più precise e aggiornate, e che tengono conto delle perturbazioni periodiche. Lo abbiamo fatto nel 1997-1999 usando il software Turbo-Sky e anche un software più preciso.Per i calcoli precisi abbiamo usato la famosa applicazione PLANETUP. I suoi autori sono J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze, G. Francou e J. Laskar (Bureau des Longitudes, URA 707. 77, Avenue Denfert-Rochereau 75014, Parigi, Francia). Viene usato per calcolare le coordinate eliocentriche, i raggi vettori e le velocità istantanee degli 8 pianeti principali del Sistema Solare (PLANETUP, Fortran 77) - Astron. Astrophys, 282 e 663 (1994).
Questo software consente di determinare le condizioni di visibilità dei corpi celesti in relazione all'orizzonte locale per qualsiasi posizione sulla Terra, a seconda del tempo e del luogo di osservazione. Può quindi essere utilizzato per la verifica di quei dettagli trovati nelle descrizioni degli oscuramenti di Tolomeo, tipo il momento della giornata (mattina, alba, sera, ecc.). I nostri precedenti calcoli meno precisi non ci hanno permesso di tener conto di questi dettagli.