Глава 3
А ТЕПЕРЬ РАССКАЗЫВАЕТ АНАТОЛИЙ ФОМЕНКО.
5. РЕШЕНИЕ ПРОБЛЕМЫ ПЛАТО В КЛАССЕ СПЕКТРАЛЬНЫХ ПОВЕРХНОСТЕЙ. РАННЯЯ ЗАЩИТА ДОКТОРСКОЙ ДИССЕРТАЦИИ.
1972 год
Защитил докторскую диссертацию 29 сентября 1972 г. В ней была решена важная проблема Плато в классе спектральных поверхностей. Тема диссертации: "Решение многомерной проблемы Плато в римановых многообразиях". Перед защитой неоднократно рассказывал эти свои результаты на семинарах кафедры дифференциальной геометрии и на семинарах ведущих наших математиков на других кафедрах. В частности, на известном семинаре выдающегося математика Марка Иосифовича Вишика. Он с большим интересом отнесся к моей работе. Потом мы с ним неоднократно обсуждали разные задачи из области геометрии и дифференциальных уравнений. На рис.3.28 – мы с ним в Воронежской Зимней Математической Школе.
– мы с ним в Воронежской Зимней Математической Школе.
На момент моей защиты два математика - А.Т.Фоменко и Евгений Михайлович Никишин, рис.3.28-0 (тоже мехмат МГУ), - оказались самыми молодыми докторами наук вообще в СССР. Мне было 27 лет. Оппоненты по моей диссертации - известные математики: Михаил Михайлович Постников, Владимир Михайлович Алексеев и Дмитрий Викторович Аносов. Внешний отзыв пришел из Ленинградского отделения математического института им. В.А.Стеклова. Этот отзыв давал известнейший математик-тополог Владимир Абрамович Рохлин, рис.3.28a
(тоже мехмат МГУ), - оказались самыми молодыми докторами наук вообще в СССР. Мне было 27 лет. Оппоненты по моей диссертации - известные математики: Михаил Михайлович Постников, Владимир Михайлович Алексеев и Дмитрий Викторович Аносов. Внешний отзыв пришел из Ленинградского отделения математического института им. В.А.Стеклова. Этот отзыв давал известнейший математик-тополог Владимир Абрамович Рохлин, рис.3.28a . Несколько раз бывал у него в Ленинграде, в том числе и дома, рассказывал о своих работах.
. Несколько раз бывал у него в Ленинграде, в том числе и дома, рассказывал о своих работах.
Итак, все мои оппоненты по диссертации – выдающиеся математики. На рис.3.29 , рис.3.30
, рис.3.30 ,
рис.3.31
,
рис.3.31 ,
рис.3.32
,
рис.3.32 ,
рис.3.33
,
рис.3.33 ,
рис.3.34
,
рис.3.34 ,
рис.3.35
,
рис.3.35 ,
рис.3.36
,
рис.3.36 , рис.3.37
, рис.3.37 , представлены некоторые моменты моей докторской защиты в МГУ, на мехмате, в большой аудитории 14-08. Голосование было положительным и единогласным. Вот фрагменты из стенограммы.
, представлены некоторые моменты моей докторской защиты в МГУ, на мехмате, в большой аудитории 14-08. Голосование было положительным и единогласным. Вот фрагменты из стенограммы.
М.М.Постников. - <<Задача Плато (о заклейке данного контура минимальной поверхностью) является одной из немногих классических задач, поставленная еще в XIX веке (150 лет тому назад) и несмотря на усилия многих выдающихся математиков, не получила до сих пор удовлетворительного решения. В рассматриваемой диссертации для этой задачи получено полное и окончательное решение в классе "спектральных поверхностей". Успех, достигнутый автором, определился не только тем, что он воспользовался всем обширным аппаратом современной алгебраической топологии, а и тем, что он понял внутренние геометрические причины неуспеха других исследователей. Автору диссертации удалось открыть новый геометрический факт - вопреки очевидности, что для улавливания некоторых естественных геометрических ситуаций обычных теорий бордизмов недостаточно, и необходимы, так называемые "бордизмы по модулю". Это позволило сформулировать "задачу Плато" для любой экстраординарной (спектральной) теории гомологий и даже (ко)гомологий. Автор решает задачу в этой общей постановке...
Первая глава имеет по существу чисто алгебраически-топологический характер. Здесь автор демонстрирует блестящее владение техникой алгебраической топологии. Центральной главой диссертации остается глава II, в которой доказывается основная теорема существования, непосредственным построением минимизирующей последовательности и доказательством ее сходимости. Уже эта часть диссертации с избытком удовлетворяет всем мыслимым требованиям, которые можно разумным образом предъявить к докторской диссертации. Поэтому нет необходимости останавливаться на главе III, которая сама по себе является полноценной докторской диссертацией. При написании диссертации перед автором стояла трудная проблема. Диссертант затратил много труда, чтобы по возможности облегчить труд читателя и в литературном отношении диссертацию сделать весьма качественной. Рассматриваемая диссертация является выдающимся научным трудом, содержащим принципиально новые результаты в очень трудной классической области, имеющие окончательный характер>>.
Д.В.Аносов. - <<Предложена обобщенная постановка многомерной задачи Плато. Доказана теорема существования минимального компакта при этой обобщенной постановке задачи и его регулярности всюду. Получена оценка минимальных компактов, реализующих циклы и т.д. Полученные диссертантом результаты едва ли нуждаются в особых комментариях, так как они являются новыми и очень сильными при любой, сколько угодно классической оценке задачи. Диссертация является ценным вкладом в науку и безусловно удовлетворяет самым строгим требованиям>>.
В.М.Алексеев. - <<В диссертации решена весьма важная и интересная математическая проблема (многомерная задача Плато в классе "спектральных поверхностей"). Автором предложено обобщение классической задачи Плато, которое естественно увязывает ее с современными разделами топологии. Для этой обобщенной постановки автором получена теорема существования. Разработанные диссертантом методы и их конструкции позволяют эффективно находить решение задачи минимизации в важном классе конкретных примеров и получать информацию о дифференциально-геометрических и топологических свойствах изучаемых объектов. Рассматриваемая диссертация удовлетворяет всем требованиям, предъявляемым к диссертациям>>.
Далее выступил академик П.С.Александров. В частности он сказал:
- <<Мне кажется, что имеется довольно общеизвестная истина, что основное бедствие, которое испытывает математика и которое влияет на большинство других наук, заключается в чрезвычайном количественном, а не качественном росте разобщенных работ. И в общем это "грандиозное строительство" несколько напоминает строительство Вавилонской башни, результатом которого было то, что строители заговорили на разных языках и потеряли способность понимать друг друга, на чем это строительство, как это написано в Библии, и закончилось. Боюсь, что нечто подобное происходит сейчас в математике. Чтобы избежать этого, необходимо усилия наших исследователей направить на решение таких проблем, чтобы поводом для исследования было не желание написать какую-то работу, защитить ее и добиться того, чтобы его процитировали коллеги, а на действительно честную потребность в решении чего-то существенного, обогащающего науку...
Хочу сказать, что рассматриваемая работа (я даже не хочу называть ее диссертацией потому, что один из оппонентов уже сказал, что эта работа есть совокупность двух докторских диссертаций) - демонстрирует здесь по существу сочетание чистого интереса к науке и прекрасного вкуса в этой научной честности. Широта познания, а также интересы диссертанта сыграли весьма существенную роль в полученных результатах, потому что из того, что здесь говорилось, можно усмотреть, что тут происходит чрезвычайно увлекательная игра между геометрическими и алгебраическими, по существу, теоретико-множественными понятиями. И я думаю, что без такого владения всеми основными направлениями в современной топологии, в современной геометрии и направлениями современной алгебры, в направлении классической формы, и в направлении теоретико-множественном, - не владей автор работы всеми этими вещами, едва ли он мог бы найти пути, которые ведут к решению поставленной задачи, и едва ли он мог бы поставить эту задачу так, как ее нужно было поставить и как он ее поставил. И недаром тут было сказано, что эта теория обращена ко всей математике. Так вот, эту поглощающую все работу, автор проделал в полной мере и с большим увлечением нам доложил ее здесь...
И все мы прекрасно понимаем, что работа диссертанта - это большой шаг вперед, сделанный в науке математике, и что автор ее не только достоин степени доктора, но он достоин еще гораздо более высокого звания, звания настоящего математика, настоящего ученого и настоящего представителя своей науки. Вот то впечатление, которое я вынес от этой защиты и которым хотел поделиться с вами, членами Ученого Совета>>. (Конец цитаты).
Теперь вкратце и наглядно объясню - что такое "проблема Плато", и что, собственно говоря, мне удалось сделать. Когда бельгийский физик Жозеф Плато в XIX веке начал опыты по изучению конфигурации мыльных пленок, он вряд ли предполагал, что они послужат толчком к развитию целого научного направления, бурно развивающегося до настоящего времени и известного под названием "проблема Плато". Опыты Плато хорошо знакомы нам с детства - это выдувание мыльных пузырей или конструирование мыльных пленок, затягивающих проволочный контур. Берем гибкую тонкую проволоку, туалетное мыло и миску воды. Растворяем мыло в теплой воде, добавляем ложку глицерина. Из проволоки делаем замкнутый контур с ручкой. Опускаем его в мыльный раствор и осторожно вынимаем. На нем повисает красивая радужная мыльная пленка, ограниченная этим контуром. Замысловато изгибая контур, можно получать самые разнообразные формы пленок. Физический принцип, лежащий в основе возникновения мыльных пленок, достаточно прост: физическая система сохраняет свою конфигурацию только в том случае, когда она не может легко изменить ее, заняв положение с меньшим значением энергии. Энергия мыльной пленки пропорциональна ее площади. Поэтому жидкая пленка превращается в эластичную поверхность, стремящуюся минимизировать свою площадь, и, следовательно, минимизировать энергию натяжения, приходящуюся на единицу площади. Минимальные поверхности встречаются в живой природе и физике как поверхности раздела двух сред с одинаковым давлением, находящихся в равновесии.
Таким образом, математической моделью мыльной пленки служит гладкая (или кусочно-гладкая) поверхность минимальной площади, затягивающая данный контур, рис.3.38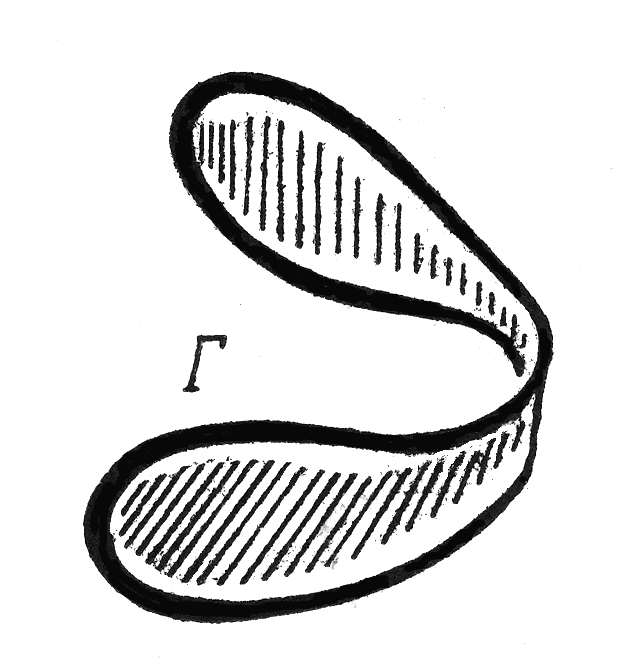 . Математики называют ее минимальной поверхностью. Такие поверхности являются математическим объектом, достаточно хорошо моделирующим физические мыльные пленки. Математическая теория минимальных поверхностей относится к так называемому вариационному исчислению - области анализа и геометрии, возникшей в XVIII веке. В наши дни для развития теории минимальных поверхностей привлекаются современные средства топологии и дифференциальной геометрии. Это богатая и сложная наука. Здесь переплетаются теории дифференциальных уравнений, групп Ли, гомологий и когомологий, бордизмов и т.д.
. Математики называют ее минимальной поверхностью. Такие поверхности являются математическим объектом, достаточно хорошо моделирующим физические мыльные пленки. Математическая теория минимальных поверхностей относится к так называемому вариационному исчислению - области анализа и геометрии, возникшей в XVIII веке. В наши дни для развития теории минимальных поверхностей привлекаются современные средства топологии и дифференциальной геометрии. Это богатая и сложная наука. Здесь переплетаются теории дифференциальных уравнений, групп Ли, гомологий и когомологий, бордизмов и т.д.
Рассмотрим сначала простой случай, когда контур не слишком сильно изогнут – а именно, когда его можно взаимно-однозначно спроектировать на выпуклый контур, лежащий в некоторой плоскости. Тогда, оказывается, существует одна и только одна минимальная поверхность, затягивающая данный контур. Если же не ограничиваться простейшими контурами, то теорема единственности перестает быть верной: на один и тот же контур иногда можно натянуть несколько совсем разных минимальных поверхностей, рис.3.39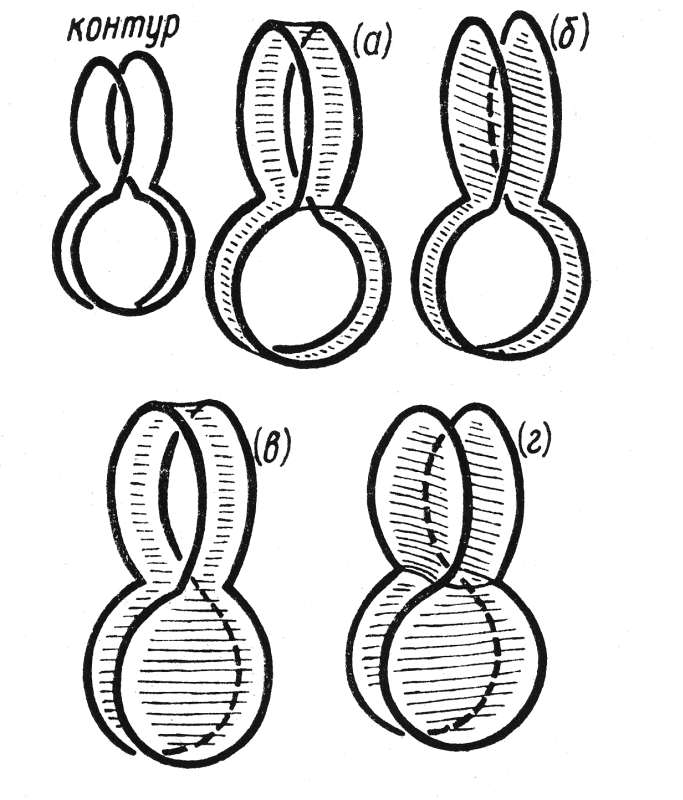 .
.
Если сильно запутать контур (например, заузлить его), то не только может нарушиться единственность пленки, но и сама ее структура может сильно усложниться. В общем случае "почти наверняка" появляются особые точки (сингулярности), то есть такие точки, в окрестности которых пленка уже не устроена, как слегка изогнутый диск, а имеет более сложную, ветвящуюся структуру, рис.3.40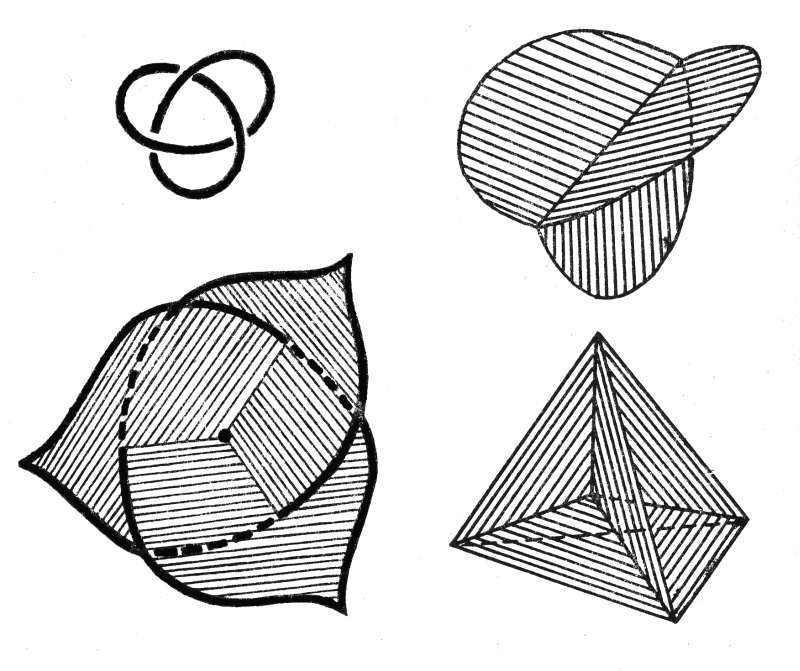 , рис.3.41
, рис.3.41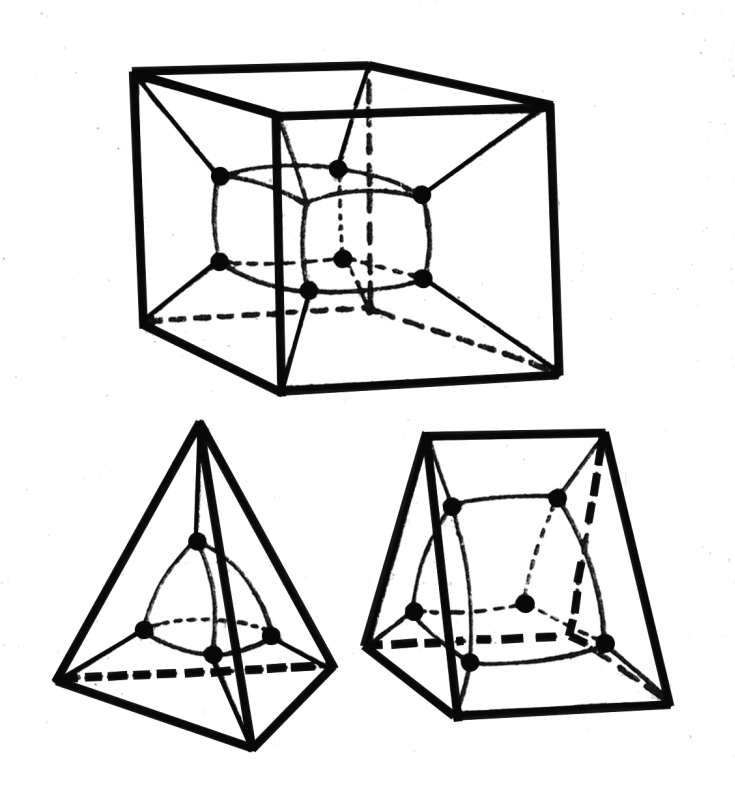 , рис.3.42
, рис.3.42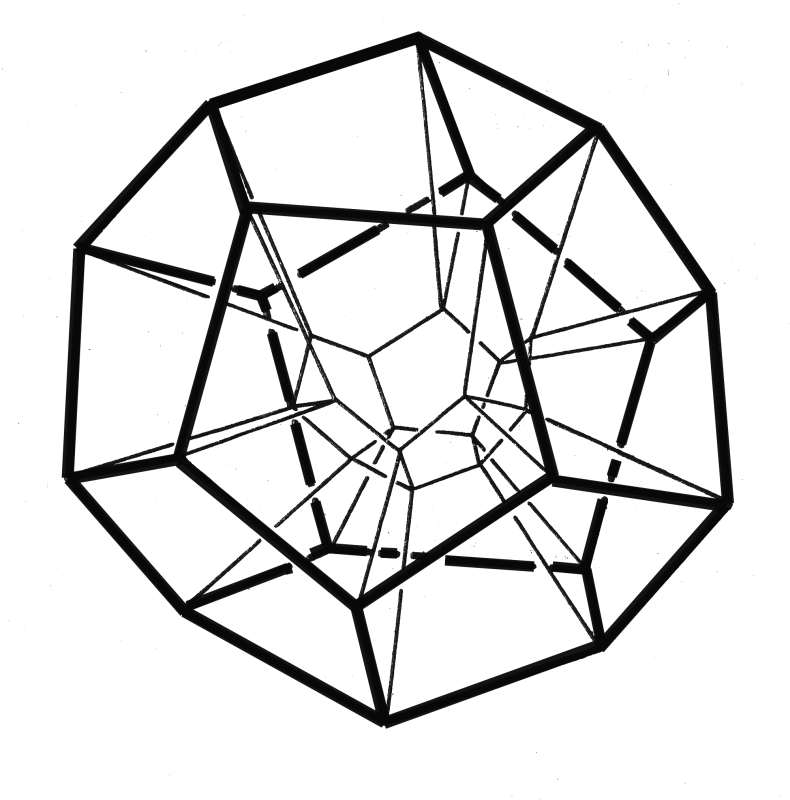 .
.
Оказывается, минимальные поверхности широко распространены в природе. Например, как наиболее экономные поверхности, формирующие скелеты некоторых живых организмов. Весьма эффектный пример особенностей минимальных поверхностей дают скелеты радиолярий, микроскопических морских животных, имеющих самые разнообразные и экзотические формы. Радиолярии состоят из небольших комочков протоплазмы, заключенных в пенообразные формы, наподобие мыльных пузырей и пленок. Минимальные поверхности, образующиеся в радиоляриях, имеют много особых точек и ребер ветвления, на которых и концентрируется основная масса жидкости, входящей в состав организма. Здесь жидкость тормозится и оседает, образуя "водяные отрезки". Концентрация жидкости вдоль ребер ветвления приводит к тому, что твердые фракции морской воды и соли оседают вдоль этих ребер и постепенно образуют твердый скелет животного. После его гибели мягкие ткани распадаются и остается твердый скелет. На рис.3.43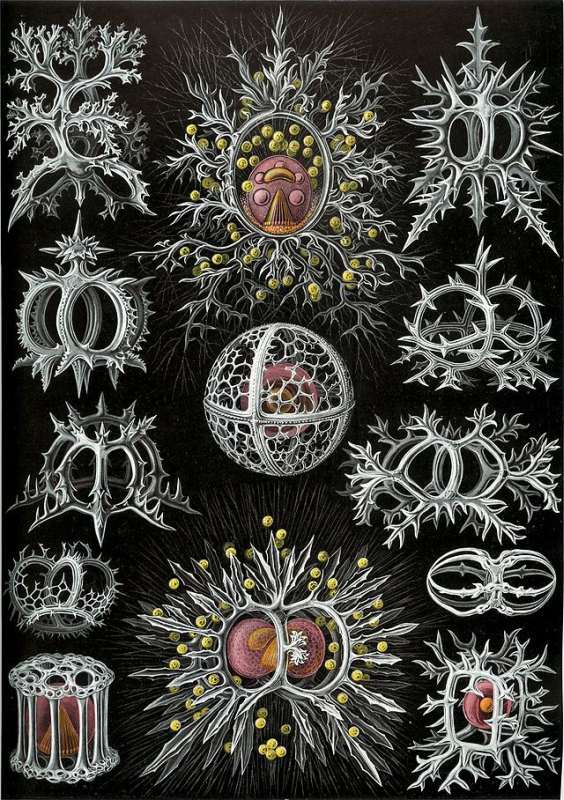 показано несколько скелетов радиолярий.
показано несколько скелетов радиолярий.
Примерами минимальных поверхностей могут служить хорошо известные мембраны - это и барабанная перепонка в нашем ухе; это мембраны, служащие границами живых клеток и т.п. В 30-е и 40-е годы XX века был достигнут большой прогресс в изучении свойств двумерных минимальных поверхностей в трехмерном пространстве. Обычно "проблема Плато" формулируется так: верно ли, что на любой замкнутый контур можно натянуть минимальную поверхность? И если "да", то - сколько таких поверхностей, и каковы их топологические свойства? С математической точки зрения это весьма непростая проблема.
Замечательные результаты в этом направлении были получены в первой половине XX века Дугласом, Радо, Курантом и др. В частности, была доказана фундаментальная теорема, утверждающая, что для любого достаточно хорошего одномерного контура (то есть, замкнутой кривой) всегда существует минимальная поверхность в трехмерном пространстве, затягивающая этот контур, причем ее площадь не превышает площади любой другой поверхности, затягивающей этот же контур.
После решения проблемы Плато для контуров в трехмерном пространстве математики перешли к "многомерной проблеме Плато". То есть вместо одномерного контура теперь рассматриваются "многомерные контуры" - замкнутые многообразия (компактные поверхности без края). Проблема звучит так: на любой ли "многомерный контур" можно натянуть минимальную поверхность (на единицу большей размерности) наименьшей возможной площади (объема)? Эта многомерная задача связана с многочисленными приложениями как в математике, так и в механике, математической физике. Многомерная проблема оказалась чрезвычайно трудной. Начиная с 60-х годов XX века в этой области произошел существенный скачок, связанный с такими именами, как: Федерер, Флеминг, Миранда, Райфенберг, Морри, Бомбьери, Джусти, Альмгрен, де Джиорджи, Саймонс, Лоусон и другие. Выяснилось, что в многомерном случае требуется сначала правильно сформулировать понятие границы и минимальной поверхности, затягивающей эту границу. Для этого был привлечен язык теории гомологий, что позволило доказать теорему существования глобально минимальной поверхности для заданного "гомологического контура" (замечательные результаты Райфенберга, Федерера и других).
Что сделал я? Мне удалось решить многомерную проблему Плато в постановке, весьма близкой к классической двумерной. А именно - в качестве "контура" рассматривается произвольное замкнутое компактное многообразие (без края), а в качестве "поверхностей" = «пленок», имеющих его своей "границей", рассматриваются компактные множества, являющиеся непрерывными образами гладких многообразий с заданным краем-границей (таких многообразий может быть много, бесконечное число).
Такие «пленки» сами могут не являться многообразиями, поскольку могут иметь сложные, «запутанные» особенности. Но эти множества «параметризованы многообразиями». Оказалось, что в классе таких компактов = "спектральных поверхностей" всегда существует глобально минимальная поверхность, затягивающая заданный "контур". На самом деле, этот мой результат является частным случаем куда более общей теории, построенной мною, в которой "спектральная проблема Плато" успешно решена в классах "параметризованных поверхностей" с заранее фиксированной границей, то есть затягивающих "контур" в смысле обобщенных (спектральных) гомологий или когомологий. Оказалось, что всегда существует многомерная минимальная "пленка", то есть имеющая наименьший объем в классе поверхностей с той же границей. Нетривиальным фактом оказалось, что такие минимальные поверхности могут состоять из «кусков» (стратов) различных размерностей, каждый из которых тоже минимален.
Доказанный мною результат оказался технически достаточно сложным. Успех был достигнут благодаря неожиданному для многих математиков новому подходу. Для решения многомерной проблемы Плато я привлек язык и технику обобщенных (спектральных) гомологий и когомологий. В частности, теорию бордизмов.
Статья Роберта Ньютона о вычислении D" опубликована в 1972 г. Newton R.R. "Astronomical evidence concerning non-gravitational forces in the Earth-Moon system". - Astrophys. Space Sci. 1972, vol.16, pp.179-200. Эта статья сыграла заметную роль в начале моих исследований хронологии, см. 1973 год.
ПУБЛИКАЦИИ ПО МАТЕМАТИКЕ:
#14 Фоменко А.Т. "Вполне геодезические модели циклов". - Труды семинара по векторному и тензорному анализу. М., изд-во МГУ, 1972, вып.16, с.14-98.
#15 Фоменко А.Т. "Многомерная задача Плато на римановых многообразиях". - Тезисы VI Всесоюзной топологической конференции. Тбилиси. Матем. Ин-т им.В.А.Стеклова, Матем. Ин-т им.А.М.Размадзе, 1972, с.120.
#16 Фоменко А.Т. "Минимальные компакты в римановых многообразиях и гипотеза Райфенберга". - Известия АН СССР. 1972, т.36, No.5, с.1049-1080.
#17 Фоменко А.Т. "Многомерная задача Плато в римановых многообразиях". - Математический Сборник. 1972, т.89, вып.3, с.475-520.
СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)
1972 год, 6 октября. Газета "Известия". Заметка "МГУ: мозаика новостей". Сообщается о молодом докторе наук в 27 лет - А.Т.Фоменко. 1972 год, 7 октября. Газета "Известия". Заметка "МГУ: только факты". Сообщение о блестящей защите А.Т.Фоменко докторской диссертации в 27 лет. В частности, сказано: <<Анатолий закончил университет всего пять лет назад. В конце 1970 года успешно защитил кандидатскую диссертацию. И вот новый успех, о котором академик Герой Социалистического Труда П.Александров сказал: - Диссертация Фоменко "Задача Плато на римановых многообразиях" - очень серьезное, большое исследование...>>. 1972 год, 17 октября. Газета "Московский Университет". Статья "Доктор наук в 27 лет" об успешной защите А.Т.Фоменко докторской диссертации. 1972 год, 23 октября. Газета "Вечерняя Москва". Статья В.Костина "Доктор точных наук" о молодом ученом МГУ А.Т.Фоменко, его лекциях и увлечениях. 1972 год, 8 декабря. Газета "Московский Комсомолец". Сообщение об успешной защите докторской диссертации А.Т.Фоменко, краткая его биография, число опубликованных работ, увлечения музыкой и живописью. Приведены две его фотографии: Фоменко у мольберта и Фоменко читает лекцию студентам МГУ.
1973 год
Мне случайно попадается статья Роберта Ньютона о загадочном скачке в поведении второй производной D" лунной элонгации, опубликованная в 1972 году, см. выше. Примерно в это же время происходит научная конференция "Место астрономии в древнем мире", организованная Британским Королевским Обществом и Британской Академией (но я пока о ней ничего не знаю). Участники конференции бурно обсуждали причину обнаруженного Ньютоном непонятного скачка D", но не пришли ни к какому определенному выводу. Начинаю работу над проблемой D", опираясь на статью Р.Ньютона. В то время я интересовался также вопросами небесной механики, посещал, как уже говорилось, семинары член-корреспондента Дмитрия Евгеньевича Охоцимского (потом академика с 1991 года) и профессора (в будущем - академика, с 1992 года) Валентина Витальевича Румянцева.
Обращаю внимание на то, что в основе вычисления Робертом Ньютоном значений параметра D" лежат даты древних затмений, взятые им из традиционных хронологических таблиц, составленных историками. И тут я вспоминаю разговоры на мехмате, что ученый-энциклопедист Н.А.Морозов, почетный академик АН СССР, как-то совсем по-иному датировал древние затмения, указывая на крупные ошибки предыдущих историков астрономии. Обращаюсь к М.М.Постникову и прошу у него тот том Морозова, где по-новому датируются старинные затмения, рис.3.44 . Получаю этот том и внимательно изучаю раздел о датировке старинных затмений. Выясняется, что многие "античные" и средневековые затмения в действительности (то есть при точном и объективном подходе) датируются астрономически куда более поздними эпохами, то есть значительно более близкими к нашему времени, чем сегодня считается.
. Получаю этот том и внимательно изучаю раздел о датировке старинных затмений. Выясняется, что многие "античные" и средневековые затмения в действительности (то есть при точном и объективном подходе) датируются астрономически куда более поздними эпохами, то есть значительно более близкими к нашему времени, чем сегодня считается.
ПУБЛИКАЦИИ ПО МАТЕМАТИКЕ:
#18 Фоменко А.Т. "Многомерная задача Плато на римановых многообразиях". - Математические Заметки. 1973, т.13, No.1, с.159-167.
#19 Фоменко А.Т. "Геометрические вариационные задачи". - Сборник "Современные проблемы математики". В серии: "Итоги науки и техники". - М., ВИНИТИ, 1973, с.39-60.
СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)
1973 год, 4 января. Чехословацкая газета "Руде Право" приводит краткую биографию Фоменко, его успехи и фотоснимок: Фоменко читает лекцию студентам МГУ. 1973 год, 19 апреля. Газета "Вечерняя Москва". Сообщение Н.Кузьмина об успешном решении А.Т.Фоменко задачи Плато, защите докторской диссертации в 27 лет и увлеченности Фоменко живописью. Приведен снимок: Анатолий Фоменко у мольберта.
6. ВСЕМИРНЫЙ МАТЕМАТИЧЕСКИЙ КОНГРЕСС 1974 ГОДА. НЕБЕСНАЯ МЕХАНИКА И ХРОНОЛОГИЯ.
1974 год
Делаю приглашенный пленарный доклад на Международном Математическом Конгрессе в Канаде, г.Ванкувер (21-29 августа). Получить приглашение сделать такой доклад на Конгрессе было всегда очень престижно. Рассказываю о своем решении спектральной проблемы Плато. Доклад вызвал большой интерес и обсуждение. В зале много народа. Получил приглашения посетить различные университеты Канады и США, чтобы подробнее рассказать о моих результатах. Некоторые из этих моих выступлений были записаны на видео для показа математикам и студентам, которые не смогли присутствовать. В частности, меня пригласил к себе в Принстон американский математик Фредерик Альмгрен, специалист в области вариационного исчисления. Мы с ним обсуждали многие вопросы теории минимальных поверхностей. На конгрессе в Ванкувере меня попросили также сделать еще один доклад, на этот раз - о достижениях других московских математиков в области алгебраической топологии. Выступил с таким дополнительным докладом, вызвавшим большой интерес у многих участников конгресса.
Занял должность старшего научного сотрудника на мехмате в мае 1974 г.
Удостоин Премии Московского Математического Общества (ММО) в 1974 г. Считается престижной премией в области математики.
В этом году мне попадается только что вышедший в свет обзор 1974 года научной конференции о проблеме D": "The place of astronomy in the ancient world". – A discussion organized jointly for the Royal Society and the British Academy. Philos. Trans. of the Royal. Soc. of London. Ser. A. 1974. Vol.276, pp.1-276. Мой интерес к работе Р.Ньютона и хронологии существенно усиливается. Учитывая детальные астрономические вычисления Н.А.Морозова, начинаю понимать, что всё дело, вероятно, в неправильных датировках старинных затмений предыдущими историками астрономии. Пересчитываю заново параметр D", пользуясь алгоритмом Р.Ньютона, но опираясь теперь на новые датировки старинных затмений, полученные Н.А.Морозовым. И совершенно неожиданно обнаруживаю, что странный разрыв в поведении D" полностью исчезает и, тем самым, на этом новом пути решается проблема загадочного скачка D". Хорошо помню, что меня это поразило. Оказывается, никакого скачка в действительности не было. Однако тут же возникает серьезное недоумение по поводу исторической хронологии. Кто же прав – история или астрономия? Специалистом в истории себя не считал, поэтому сразу обратился к ведущим историкам нашего ист-фака МГУ. Беседа с ними, в частности, с известным профессором-историком В.И.Кузищиным, показала, что вопросами хронологии современные историки не занимаются (как они сами мне сказали), то есть заученно ссылаются "на традицию". Хронологию считают вспомогательной, второстепенной дисциплиной. Мне посоветовали (В.И.Кузищин) «в это не влезать и заниматься математикой, которая у вас хорошо получается». Стало ясно, что с хронологией древности что-то серьезно не так. Начинаю изучать вопрос самостоятельно, более глубоко. На это уходит довольно много времени. Ввиду неясности картины в целом, пока что не отдаю в печать свои уже готовые математические исследования по D" (ускорению Луны). Хочу разобраться более детально.
В 1974 году обращаюсь к М.М.Постникову с просьбой сделать для меня и созванных мною нескольких заинтересовавшихся математиков (среди которых был Александр Сергеевич Мищенко) обзор основных исследований Морозова. Постников прочел нам у себя дома пять лекций по книгам Морозова. С согласия Постникова записал его лекции на магнитофон, специально купленный мною для этой цели. Потом сам надиктовал несколько (около десятка) дополнительных (часовых) кассет с моими собственными дополнениями, соображениями и постановками задач по хронологии. Давал слушать эти кассеты интересующимся. Довольно много коллег, студентов и аспирантов МГУ (отнюдь не только математики) брали потом их у меня и даже переписывали себе. Эти записи довольно широко распространились в научной среде.
Беру на время у М.М.Постникова все семь томов морозовского "Христа", анализирую их. Через несколько лет мне подарили все тома Морозова, кроме одного, шестого. Надо сказать, что книги Морозова уже давно стали антикварной редкостью. Потом мне удалось сделать для себя ксерокопию и шестого тома. Кстати, в то время сделать у нас в стране ксерокопию книги было вовсе не так просто – требовалось получить официальное разрешение.
Между прочим, первоначальное название морозовского труда «Христос» было совсем другим (и, как потом стало понятно, куда более правильным): «История человеческой культуры в естественно-научном освещении». Попутно начинаю разработку новых методов датирования событий, опирающихся на математику и статистику. Поскольку, как обнаруживается, традиционные методы археологов и историков либо допускают значительные ошибки, либо покоятся на предполагаемой заранее известной (и ошибочной) хронологии Скалигера-Петавиуса, созданной в XVI-XVII веках. А потому вовсе не являются объективными, независимыми. Нужен качественно новый подход, нужны новые методы – математические, статистические, астрономические.
ВЫСТАВКИ МОИХ РАБОТ: 1974, 23 декабря. Моя персональная выставка в Доме Книги, Москва, Калининский проспект. На заседании клуба Книголюбов. Выставлено 40 моих работ. Выставка организована изд-вом "Наука", по инициативе математиков - академика АПН СССР Алексея Ивановича Маркушевича и профессора Бориса Владимировича Шабата. 1974, 30 ноября - 1 декабря. Моя персональная выставка в ДАС'е (Дом Аспирантов и Стажеров при МГУ, 1 этаж, читальный зал). Выставлено 130 моих работ. Выставка организована аспирантским Советом МГУ и Советом ДАС'а.
ПУБЛИКАЦИИ ПО МАТЕМАТИКЕ:
#20 Фоменко А.Т. "Многомерные задачи Плато на римановых многообразиях". Часть 1. - Труды семинара по векторному и тензорному анализу. - М., изд-во МГУ, 1974, вып.17, с.3-176.
#21 Володин И.А., Кузнецов В.Е., Фоменко А.Т. "О проблеме алгоритмического распознавания стандартной трехмерной сферы". - Успехи математических наук, 1974, т.24, вып.5, с.71-168.
#22 Fomenko A.T. "Multidimensional Plateau problem on Riemannian manifolds. On the problem of the algorithmical recognizability of the standard three-dimensional sphere". - Proc. of the Intern. Congress of Math. 1974, Vancouver, v.1, pp.515-525.
#23 Новиков С.П., Фоменко А.Т. "Дифференциальная геометрия". Часть 3. (Учебное пособие). - М., изд-во МГУ, 1974.
СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)
1974 год, 19 марта. Газета "Московский Университет". Статья "Мехмат воспитывает таланты", в которой дана характеристика талантливым ученым, окончившим МГУ. В том числе и А.Фоменко. В этой же газете помещена статья "Алгебру гармонией проверить". 1974 год, 20 июля. Газета "Социалистическая индустрия". Статья Н.Медведевой "Всё вокруг математики". Об А.Т.Фоменко и его работах, с его портретом и одной работой. 1974 год, май. Передача Центрального Телевидения "Москва и москвичи". Об ученых МГУ, в том числе об А.Фоменко.
1975 год
Вместе с моим коллегой Александром Сергеевичем Мищенко сделали яркую работу в области интегрируемых гамильтоновых систем. Мы обнаружили глубокий алгебро-геометрический факт. Доказали, что уравнения движения так называемого "многомерного твердого тела" и, что еще важнее, далеко идущие естественные обобщения этих уравнений на полупростых группах и алгебрах Ли, - вполне интегрируемы по Лиувиллю. То есть допускают простое и эффективное описание интегральных траекторий (решений). Эта работа вышла в свет в следующем 1976 году. Именно в этой работе был развит новый метод, существенно обобщающий идею С.В.Манакова, и получивший потом название "метода сдвига аргумента". А обнаруженные нами коммутативные полные наборы интегралов таких гамильтоновых уравнений получили позже название "алгебры Мищенко-Фоменко". Эта наша работа с А.С.Мищенко породила целый цикл исследований интегрируемых систем на алгебрах и группах Ли. В частности, многие мои ученики внесли большой вклад в развитие этой теории. В дальнейшем наши работы развивались другими математиками, например, алгебраистом Эрнестом Борисовичем Винбергом и его учениками.
Мы обсуждали эти сюжеты также с известным алгебраистом, член-корреспондентом АН СССР, Кострикиным Алексеем Ивановичем. Скажу здесь, что у меня с ним с самого начала сложились теплые дружеские отношения.
А теперь – о хронологии. Пишу письмо Р.Ньютону с сообщением о моем решении проблемы D". Быстро получаю от него заинтересованный, но явно растерянный ответ. Он согласен с математической сутью моего исследования, но не понимает - а как же тогда быть с традиционной хронологией, которой он ранее полностью доверял. Я постарался кратко объяснить ему, насколько это возможно в рамках нескольких писем. Р.Ньютон ответил, что попытается разобраться в проблеме хронологии, хотя он далек от истории. Но наша переписка была непродолжительной и развития не получила. Потом, уже после смерти Р.Ньютона, его вдова прислала мне некролог из американской газеты с его портретом.
В начале 1975 года М.М.Постников, А.Т.Фоменко и А.С.Мищенко договорились написать критический текст, посвященный исследованию древней хронологии. В частности, мы хотели кратко изложить объемистый семитомный труд Морозова "Христос", очистить его от большого количества "воды". Было решено, что фактически книгу напишут Фоменко и Мищенко, а Постников выступит как редактор и напишет краткий раздел по истории Китая и про лингвистику. Работая на протяжении практически всего года, Фоменко и Мищенко такой текст создали. В основном эта книга была написана мною. Затем я собственноручно отпечатал ее на пишущей машинке. Всего в ней оказалось около 2000 (двух тысяч) машинописных страниц. В сентябре 1975 года машинописная рукопись была передана Постникову. При этом договорились, что никакой существенной правки в уже написанном нами тексте Постников делать не будет, лишь добавит свой материал. Постников начал редактирование и сказал, что покажет нам только окончательную версию. Мы согласились ждать.
ВЫСТАВКИ МОИХ РАБОТ: 1975, 16 ноября. Моя персональная выставка в главном здании МГУ, общежитие зоны Б, гостиная Б-4. Выставлено 97 работ. Организована студкомом физического ф-та МГУ. Организаторы: физики Виктор Васильевич Мощалков и Энно Йоон. Кстати, В.В.Мощалков потом переехал с семьей жить и работать в Бельгию, в город Leuven, в Католический университет города Лёвена. Он стал известным физиком, руководителем отдела физики низких температур, видным администратором, лауреатом самой престижной в Бельгии Премии в области науки, вручаемой самим королем.
СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ) 1975 год, 1 сентября. Газета "Московский Университет". Статья Николаевой "Молодость не препятствие". О молодых ученых, в частности, о А.Фоменко, защитившем докторскую диссертацию в 27 лет.
1976 год
Вышла из печати моя работа с А.С.Мищенко о полном интегрировании по Лиувиллю гамильтоновых систем на орбитах полупростых альгебр Ли, полученных сдвигом аргумента у инвариантов этих алгебр. Этот результат явился началом богатой алгебро-геометрической теории подобных динамических систем. Оказалось, что класс таких систем включает важные уравнения, возникающие в математической физике и теоретической механике. Мы с Мищенко сформулировали гипотезу о том, что на произвольной конечномерной алгебре Ли всегда существует "полный коммутативный набор полиномов", то есть всегда существует интегрируемая полиномиальная гамильтонова система с полным набором полиномиальных интегралов. В нашей работе эта гипотеза была доказана для широкого класса полупростых и редуктивных алгебр Ли. Затем, через несколько лет, для оставшихся алгебр Ли гипотеза была окончательно доказана С.Т.Садэтовым. В итоге появилась важная теорема Мищенко-Фоменко-Садэтова.
Разрабатываю новые эмпирико-статистические методы датирования. Начинаю создавать ГХК - глобальную хронологическую карту. Проверяю результаты Морозова, заново пересчитываю датировки некоторых старинных затмений, упомянутых в летописях. Мне начинают помогать некоторые коллеги-математики. В том числе несколько студентов и аспирантов (с других кафедр). Кстати, своих непосредственных учеников и коллег по кафедре никогда не втягивал в эту деятельность. Напротив, старался вообще не обсуждать с ними тему хронологии. Как неожиданно оказалось, тема эта очень острая. Многие коллеги из МГУ выражали большой интерес. Некоторые пугливо сторонились. Кое-кто бурно возмущался. В общем, эмоций было много.
Прошло около года после того, как мы с Мищенко вручили Постникову рукопись нашей книги. Лишь в сентябре 1976 года, после настойчивых просьб, Постников, наконец, показал нам свою редакцию нашего текста. Мы ужаснулись. "Редактирование" свелось к тому, что во главу угла был поставлен неверный тезис Морозова о "выдуманности всей древней истории". Дескать, "античность была сочинена поздними писателями из головы". Постников придал этой идее даже более радикальный характер, чем это когда-то звучало у Морозова. О математических методах в хронологии практически ничего в книге не осталось. Ничего нового сам Постников к нашему тексту фактически не добавил. Мы с большим трудом забрали у него свою истерзанную рукопись, и то лишь после резкого письма, написанного мною к его жене - Светлане Эдмундовне (Постников отказывался в тот момент со мной разговаривать). Привожу здесь это мое письмо.
"16 октября 1976 года.
Глубокоуважаемая Светлана Эдмундовна!
Информирую Вас и Михаила Михайловича, что в последние три недели среди сотрудников и аспирантов механико-математического факультета распространяется слух, в котором, с прямой ссылкой на Михаила Михайловича, говорится следующее: Михаил Михайлович Постников написал книгу по истории, а А.Т.Фоменко в настоящее время препятствует работе над ней. Должен ли я, ввиду также того обстоятельства, что на мои многочисленные просьбы допустить меня к моим собственным материалам, находящимся у Михаила Михайловича, Михаил Михайлович отвечает отказом, расценивать всю эту информацию как указание на то, что с его точки зрения все мои материалы мне уже не принадлежат?
С глубоким уважением А.Т.Фоменко".
Итак, наш машинописный текст в конце концов с трудом удалось получить обратно, однако у Постникова осталась его копия. Эту отредактированную копию потом Постников превратил в книгу, на которой поставил уже только одну свою фамилию. Сначала он поместил эту рукопись в библиотеку математического института им. В.А.Стеклова как свой отчет о научной работе. В 1977 году Постников размножил рукопись в ИНИОН - всего было сделано 20 копий на ротапринте. Потом, через несколько лет, в 2000 году, он издал ее в московском изд-ве Крафт+Леан под одной своей фамилией: М.М.Постников, "Критическое исследование хронологии древнего мира". Тома 1-3, М.: Крафт+Леан, 2000 год.
В конце 1976 года мое сотрудничество с М.М.Постниковым в области хронологии практически прекратилось на довольно длительное время. Впрочем, через несколько лет, в 1982 году Постников и я издали совместную статью, посвященную анализу древней хронологии (см. ниже). Надо сказать, что М.М.Постников всегда относился весьма ревниво к моим исследованиям по хронологии и, в первую очередь, к разработанным мною новым эмпирико-статистическим методам. Сам он на протяжении нескольких лет лишь пересказывал Морозова, не добавляя ничего нового. По-видимому, это его заметно тяготило. Отсюда и некоторое напряжение, возникшее потом в наших отношениях. Но, повторю, всегда относился к нему как к выдающемуся математику, прекрасному лектору, заслуживающему всяческого уважения.
В этом же 1976 году меня познакомили с известным историком Львом Николаевичем Гумилевым. Я его глубоко уважал. Несколько раз бывал у него дома. Последняя встреча состоялась 26 июля 1977 года (об этом - ниже). Я объяснял ему суть моих исследований по хронологии. Сначала реакция Гумилева была категорически отрицательной. Впрочем, после нескольких продолжительных наших бесед, у него возник неподдельный интерес. Тогда я предложил ему прочитать некоторые мои тексты на эту тему. Он взял их на довольно длительное время, и действительно стал читать.
Руковожу музыкальным клубом Топаз. Однако сам на концертах теперь уже появляюсь редко: масса других дел.
ВЫСТАВКИ МОИХ РАБОТ: 1976, 20-27 апреля. Участие в выставке "Изобразительное и декоративно-прикладное творчество студентов и сотрудников МГУ". Организована факультетом журналистики МГУ. Ленинские Горы. Выставлено 14 работ. 1976, 26-28 ноября. Моя персональная выставка в Доме Ученых НЦ (Научного Центра) АН СССР, в Красной Пахре (Академгородок). Выставлено 40 работ. Меня пригласил известный академик-физик Е.П.Велихов. 1976, 10-12 декабря. Моя персональная выставка в Доме Метролога. Народный университет культуры ВНИИФТРИ. г.Менделеево. Выставлено 160 работ.
ПУБЛИКАЦИИ ПО МАТЕМАТИКЕ:
#24 Мищенко А.С., Фоменко А.Т. "Интегрирование уравнений Эйлера на полупростых алгебрах Ли". - Доклады АН СССР. 1976, т.231, No.3, с.536-538.
СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)
1976 год, 25 января. Газета "Правда". Статья Ю.Марущака "Вечерами у студентов" - о клубе Топаз, организованном А.Т.Фоменко. 1976 год. Газета "Московский Университет". Заметка о выставке картин А.Фоменко.