BÖLÜM 5:
ESKİ OLAYLARIN TARİHLENMESİNDE MATEMATİKSEL İSTATİSTİK YÖNTEMLERİ
2. HÜKÜMDARLARIN HANEDANLARININ SEÇİLME VE TARİHLENME YÖNTEMİ. KÜÇÜK HANEDAN TAHRİFATLARI İLKESİ
2.1. Küçük Hanedan Tahrifatları İlkesinin Formüle Edilmesi
Küçük hanedan tahrifatları ilkesi ve ona dayalı yöntem yazar tarafından [884], [885], [888], [1129], [895],[1130]’da sunulup geliştirilmiştir.
Diyelim ki, iktidar süresi belli olan hükümdarların bilmediğimiz bir hanedanını anlatan bir tarihî metin bulundu. Bu hanedanın bilmediğimiz, yeni ve bu yüzden tarihlemeyi gerektiren bir hanedan mı, yoksa sadece anlamadığımız terimlerle betimlenmiş olan bildiğimiz hanedanlardan birisi mi olduğu sorusu ortaya çıkıyor. Örneğin, hükümdarların isimlerinin değiştirilmiş biçimde kullanılması vb. Aşağıdaki yöntemler buna cevap vermektedir [904], [908], [1137], [885], [886].
Herhangi bir devletin ya da bölgenin tarihindeki gerçek hükümdarların veya kralların k sırasını ele alalım. Kolaylık sağlamak amacıyla, bu sırayı GERÇEK HANEDAN olarak adlandıralım. Ama üyeleri hiç de akraba olmak zorunda değiller. Çoğunlukla, aynı gerçek hanedan farklı belgelerde ve farklı vakanüvisler tarafından tasvir ediliyor. Hem de farklı açıdan. Mesela hükümdarların faaliyeti, ehemmiyeti, kişisel özellikleri farklı biçimde değerlendiriliyor. Bununla beraber, tasvirleri vakanüvislerin sempati ya da antipatilerine daha az bağımlı olan “değişmez” olgular da bulunmaktadır. Örnek olarak, hükümdarların iktidar süreleri bu tarz az çok “değişmez olgulara” dâhildir. Genellikle vakanüvislerin bu sayıyı önemli ölçüde veya kasıtlı olarak uzatma nedeni olmuyor. Ancak, vakanüvisler bir hükümdarın iktidar süresini (yıllarını) hesaplarken sık sık doğal güçlüklerle karşılaşıyorlardı.
Bu doğal güçlükler şunlardır: Bilginin eksikliği, belgelerdeki tahrifat vs. Bunlar bazen, farklı vakanüvislerin vakayinamelerinde ya da tablolarında kendilerine göre aynı hükümdarın iktidar süresi olarak farklı tarihler koymasına yol açıyordu. Bu tarz ayrılıklar -bazen önemlidir- mesela H. Brugsch’un tablolarındaki [99] firavunlar için ve J. Blair’in “Kronolojik Tabloları” [76] için tipiktir. Örneğin J. Blair’in XIX. yüzyıla kadar ulaşan tablolarında, bilgileri bize ulaşan bütün ana tarihî hanedanlar, hükümdarların iktidar yıllarıyla birlikte toplanmıştır. J. Blair’in tabloları bizim için Skaliger kronolojisinin yaratıldığı döneme pek yakın olduğu için kıymetlidir. Bu nedenle, bunlar “Skaliger faaliyetinin” XIX-XX. yüzyılın tarihçileri tarafından örtülen daha belirgin izlerini taşıyor.
Böylelikle bir gerçek M hanedanını tarif eden her vakanüvis kendi yolunda, kendi yeteneklerine ve imkânlarına göre hükümdarlarının iktidar yıllarını hesaplıyor. Sonuçta bir a=(a1, a2,...,ak) sayı dizisini elde ediyor. Bu formülde ai, belki de hatalı bir şekilde, i numarası altındaki hükümdarın gerçek iktidar yıllarını göstermektedir. Hatırlatalım ki, k sayısı bu hanedandaki hükümdarların genel sayısıdır. Vakayinameden çıkarılan bu sayı sırasını kolaylık sağlamak amacıyla VAKAYİNAME HANEDANI olarak adlandırıyoruz. Bunu Rk Öklid uzayında a vektörüyle göstermek uygundur.
Aynı M hanedanını tasvir eden bir başka vakanüvis aynı hükümdarlara biraz farklı iktidar yılları yazabilir. Sonuçta bir başka b2,...,bk) hanedanı ortaya çıkar. Böylece farklı vakayinamelerde tasvir edilen aynı gerçek M hanedanı farklı a ve b hanedanları sıfatıyla gösterilebilir. Bu durumda, ortaya çıkan çarpıtmaların ne kadar büyük olduğu sorusu doğar.
Burada, hatalar ve iktidar sürelerini net olarak tespit etmeyi engelleyen nesnel güçlükler büyük önem taşımaktadır. Hataların belli başlı çeşitlerini aşağıda anlatacağız.
Kolaylık sağlamak amacıyla KÜÇÜK TAHRİFAT İLKESİ olarak adlandıracağımız modeli veya varsayımı formüle edelim.
İKTİDAR YILLARININ KÜÇÜK TAFRİFAT İLKESİ. İki a ve b vakayiname hanedanı birbirinden biraz farklı ise aynı M hanedanını anlatıyor demektir, yani bunlar hanedanın tasvirinin farklı vakayinamelerdeki iki seçeneğidir. Bu durumda, vakayiname hanedanlarını BAĞIMLI olarak adlandıralım. Tersine, iki a ve b vakayiname hanedanı iki farklı gerçek M ve N hanedanını betimliyorsa birbirinden “önemli ölçüde” farklıdır. Bu durumda bunları BAĞIMSIZ olarak adlandıralım. Geriye kalan hanedan çiftlerini YANSIZ olarak adlandıralım.
Bir başka ifadeyle, bu varsayımsal modele göre, FARKLI VAKANÜVİSLER VAKAYİNAMELERİNİ YAZARKEN AYNI GERÇEK HANEDENI “BİRAZ” TAHRİF ETMİŞLERDİ. Herhalde ortaya çıkan farklılıklar, “ortalama olarak” açıkça bağımsız gerçek hanedanlar arasındaki farklılıklara göre daha küçüktü anlaşılan.
Yukarıda formüle edilen varsayım veya model deneysel denetim gerektiriyor. Haklılığı ortaya çıktığı takdirde, eski vakanüvislerin faaliyetini niteleyen önemli ve hiç de açık olmayan bir niteliği keşfetmiş olacağız: AYNI GERÇEK HANEDAN TASVİR EDİLİRKEN ORTAYA ÇIKAN VAKAYİNAME HANEDANLARI, GERÇEKTEN FARKLI İKİ HANEDAN BİRBİRİNDEN NE KADAR FARKLIYSA, BİRBİRİNDEN VE PROTOTİPİNDEN DAHA AZ FARKLIDIR.
Her a ve b vakayiname çifti için hesaplanan doğal sayısal c(a,b) katsayısı bulunmakta mıdır? Ayrıca bu katsayı bağımsız vakayinameler için “küçük” olmalı ve bağımlı vakayinameler için aksine “büyük” olmalı. Başka bir deyişle, böyle bir katsayı bağımlı ve bağımsız vakayinameleri seçip ayrım yapmalı. Bu katsayıyı bulduk.
İki a ve b hanedanının yakınlığını değerlendirmek için yukarıda betimlenen SRKO = p(Х,Y)’e benzer sayısal c(a,b) katsayısının kullanılabileceği ortaya çıkıyor. Bu c(a,b) katsayısının da olasılık anlamı var. Önce c(a,b) katsayısını bulmaya ilişkin kaba fikri anlatalım. Vakayiname hanedanını, yatay eksende hükümdarların numaralarının ve düşey eksende iktidar yıllarının konduğu grafik olarak göstermek kullanışlıdır. Diyoruz ki, q hanedanının grafiğinin a hanedanının grafiğine göre farkı, b hanedanının grafiğinin a hanedanının grafiğine göre farkından daha çok olduğu takdirde, q hanedanı a hanedanına en az b hanedanı kadar “benzer”. Bkz. aşağıya ve [904], [1137], [885], [886],[884].
b hanedanına göre a hanedanına daha çok benzeyen hanedanların bütün hanedanlar arasında oluşturduğu pay с(a,b) olarak kabul edilir. Bir başka deyişle, şu oran bulunur:
| en az b kadar a’ya “benzer” hanedanların miktarı --------------------------------------------------------------------------------. |
| vakayinamelerde tasvir edilen hanedanların genel sayısı |
Hükümdarların iktidar süreleri vakanüvisler tarafından hatalı tespit edilebilir. Fiilen vakayinamelerden yalnızca yaklaşık değerleri alıyoruz. Bu hatalara yol açan olası mekanizmaları matematiksel olarak tarif etmek mümkündür. Bunun dışında vakanüvislerin iki hatasını daha dikkate aldık: İki bitişik hükümdarın yerlerinin değiştirilmesi ve iki bitişik hükümdarın yerine bunların toplam iktidar süreleriyle bir hükümdarın konması.
c(a,b) katsayısını, kolaylık sağlamak amacıyla, HRKO, yani a ve b hanedanlarının rastlantısal kesişme olasılığı olarak adlandırabiliriz.
2.2. İstatistiksel Model
Şimdi c(a,b) katsayısının biçimsel açıklamasını verelim. k uzunluğundaki bütün gerçek hanedanların kümesini D olarak işaretleyelim. Fiilen D kümesi olarak bilgileri korunmuş vakayinamelerde bize ulaşan tarihî hanedanları almak zorunda kalacağız. Aşağıda sayılan çok sayıdaki farklı kronolojik kaynağa dayanarak, bütün bu hanedanların neredeyse tam listesini derledik. Bu kaynaklar temelinde, Skaliger kronolojisine göre M.Ö. 4000 senesinden M.S. 1900 senesine kadar Avrupa, Akdeniz bölgesi, Orta Doğu, Mısır ve Asya’da hüküm süren 15 ardışık hükümdardan ibaret olan bütün grupların listesini oluşturduk.
Her vakayiname hanedanı k boyutlu Rk Öklid uzayında vektör olarak gösterilebilir. Bizim somut deneyimizde k=15 olarak saptadık. Aynı zamanda iki hanedanın üyesi olan kralların, yani gerçek hükümdarların miktarı k/2 sayısını, yani bütün hanedanın üyelerinin yarısını aşmıyorsa, iki hanedanın önemli oranda farklı olduğunu kabul edeceğiz. İki rastgele alınmış gerçek hanedan kesişebilir, üyeleri aynı olabilir, çünkü her zaman farklı bir hükümdarı rastgele “bu hanedanın başlangıcı” olarak ilan edebiliriz. Bağımlı ve bağımsız hanedanların yanı sıra ortak krallarının, yani gerçek hükümdarlarının miktarı k/2 sayısını aşan ama bağımlı olmayan “ara”, “yansız” hanedan çiftleri de vardır. Eğer incelenen hanedanların genel miktarı büyük ise, ara, yansız hanedan çiftlerinin miktarının nispeten küçük olduğu ortadadır. Bu yüzden, dikkatimiz öncelikle bağımlı ve bağımsız hanedan çiftlerinin üzerinde olmalıdır.
Yukarıda formüle edilen küçük tahrifatlar ilkesi, vakanüvislerin fiilen “ortalama olarak” önemli olmayan hatalar yapmış olmalarına rağmen, gerçek sayısal verileri önemli oranda çarpıtmamış oldukları anlamına geliyor.
Vakanüvislerin eski hükümdarların iktidar sürelerini hesaplamada en sık yaptıkları yanlışlıkları ele alalım. Çok sayıda somut tarihî metni ele alırken, bu tarz üç çeşit yanlışlık saptadık. Bu yanlışlıkların, en sık olarak, hükümdarların iktidar sürelerinin çarpıtılmasına yol açtığı anlaşıldı.
Birinci yanlışlık. İki bitişik hükümdarın yerlerinin değiştirilmesi veya karıştırılması.
İkinci yanlışlık. İki hükümdarın yerine iktidar süresi bu iki hükümdarın toplam iktidar yıllarına eşit olan tek bir hükümdarın konması.
Üçüncü yanlışlık. Hükümdarların kendi iktidar sürelerinin hesaplanmasındaki yanlışlık. Bu süre ne kadar uzunsa vakanüvis onu hesaplarken genellikle o kadar büyük hata yapıyordu.
Bu üç çeşit yanlışlık betimlenip matematiksel olarak modellenebilir. Birinci ve ikinci yanlışlıklarla başlayalım. D kümesindeki herhangi bir p=(p1,p2,...,pk) hanedanını ele alalım. q vektörünün her qi koordinatı p vektörünün koordinatlarından aşağıdaki iki işlemin biri aracılığıyla elde ediliyorsa, q=(q1,q2,...,qk) vektörünü p vektörünün (hanedanının) SANAL VARYASYONU olarak adlandırıp q=vir(p) olarak işaretleyelim.
(1) Ya qi = pi (yani koordinat değişmez) ya da pi, pi-1 ile veya pi+1 ile, yani p
vektörünün bitişik koordinatlarından birisi ile yer değiştirir.
(2) Ya qi = pi ya da qi, pi + pi+1 katsayısı ile uyuşuyor.
Bu şekildeki her q vektörünün (hanedanının) birinci ve ikinci yanlışlıkların etkisiyle
“çoğalmış” gerçek p hanedanından çıkmış olan vakayiname hanedanı olarak algılanabilir olduğu açıktır. Bir başka deyişle, D listesinden her gerçek p=(p1,p2,...,pk) hanedanını alıp ona (1) ve (2) “tedirginliğini” uyguluyoruz. Yani ya bitişik pi ve pi+1 sayılarının yerlerini değiştiriyoruz ya da bir pi sayısının yerine pi + pi+1 veya pi-1 + pi toplamını geçiriyoruz. Her i sayısı için yukarıda sayılan işlemleri birer kere uyguluyoruz, yani aynı i noktasındaki “uzun yinelemeleri” ele almıyoruz. Sonuçta bir p hanedanından belirli bir sayıda {q=vir(p)} sanal hanedanları oluşuyor. Bu sanal hanedanların miktarını hesaplamak kolaydır.
Böylelikle D kümesindeki her “nokta” “çoğalıp” kendisinin çevresini oluşturan “sanal noktaların” belli bir miktarını, “civar bulutunu”, “küresel yığınağını” doğuruyor, res.5.16
. Ortaya çıkan sanal hanedanların bazılarına somut bir vakayinamede rastlayabiliriz (bu durumda bunlar vakayiname hanedanları olacak), bazıları ise “teorik olarak olası”, yani sanal kalmaktadır.
Bütün gerçek p hanedanlarından çıkıp D hanedan listemizi oluşturan bütün sanal hanedanları birleştirerek bir vir(D) kümesini, yani D hanedanlarının çıkış kümesini “kucaklayan bulutu” elde ediyoruz.
Böylece her gerçek M hanedanı için onu betimleyen vakayinamelerin kümesi, vir(M) “küresel yığınağı” olarak gösterilebilir. Şimdi iki gerçek M ve N hanedanını ele alalım. Formüle ettiğimiz küçük tahrifatlar ilkesi doğru ise, iki açıkça bağımsız, farklı gerçek hanedana uygun olan vir(M) ve vir(N) küresel yığınağı Rk uzayında kesişmiyor. Yani bunlar birbirinden yeterince uzak olmalı, res.5.17
.
Şimdi diyelim ki, a ve b, vir(D) kümesinden iki hanedan, örneğin iki vakayiname hanedanı, res.5.18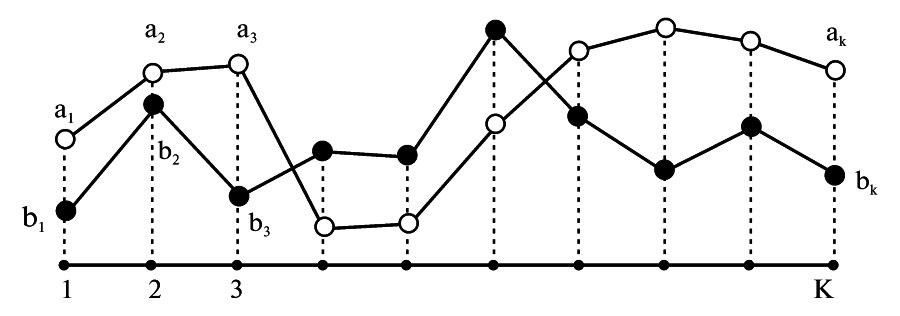
. İki hanedan arasındaki yakınlığın belli bir nicel ölçüsünü uygulamak, yani “arasındaki mesafeyi ölçmek”, birbirinden ne kadar uzak olduğunu değerlendirmek istiyoruz. En basit yol şudur. İki hanedanı Rk uzayında vektörler olarak kabul edip arasındaki Öklid uzaklığını alabiliriz, yani karesi
(a1 - b1)2 + ... + (ak - bk)2
biçiminde olan r(a,b) sayısını hesaplayabiliriz.
Ancak somut vakayiname hanedanlarıyla yapılan nicel deneyler gösteriyor ki, bu mesafe bağımsız ve bağımlı vakayinameleri birbirinden güvenilir şekilde ayırmayı mümkün kılmıyor. Başka bir ifadeyle, açıkça bağımlı hanedanlar arasındaki bu tarz mesafelerin ve açıkça bağımsız hanedanlar arasındaki mesafelerin bazı durumlarda birbiriyle karşılaştırılabilir olduğu görülüyor. Bunların bazen aynı “büyüklük sırasına” sahip olduğu ortaya çıkıyor.
Üstelik iki hanedanın, daha kesin olarak bunların iktidar grafiklerinin “benzerliği” veya “benzemezliğini” ilk bakışta tespit etmek mümkün değil. İki grafiğin görsel benzerliği hiçbir şey anlatmayabilir. Gerçekte hiçbir bağımlılık olmadığı halde, iktidar grafikleri “gayet benzer” çıkan açıkça bağımsız hanedan örnekleri verebiliriz. Görülüyor ki, görsel yakınlık bu mesele çerçevesinde kolayca yanıltıcı olabilir. “Benzer”, “benzemez” gibi kararsız subjektif düşünceleri ortadan kaldıran güvenilir bir nicel değerlendirme gerekiyor.
Yani amacımız, bütün sanal hanedanlar üzerinde bağımlı hanedanları bağımsız hanedanlardan güvenle ayırmayı veya açıkça bağımlı hanedanlar arasındaki “mesafenin” “küçük” ve açıkça bağımsız hanedanlar arasındaki “mesafenin” “büyük” olmasını mümkün kılacak doğal bir yakınlık ölçüsü bulunup bulunmadığını ortaya koymaktır. Üstelik bu “küçük” ve “büyük” değerlerin birbirinden epeyce, yani bir ya da birkaç büyüklük sırasıyla ayrılmış şekilde farklı olması gerekiyor.
Böyle bir yakınlık ölçüsünün, yani “hanedanlar arasındaki mesafe”nin gerçekte varolduğu görülüyor. Şimdi, bu c(a,b) katsayısının tasvirine geçelim.
R15 uzayında D hanedanlarının belli bir kümesini kurduk. Vakanüvislerin en sık yaptığı iki çeşit yanlışlık modellendi. D kümesindeki her hanedan (1) ve (2) yanlışlığından geçirildi. Bu durumda, D’nin her noktası bir dizi noktaya çoğalınca küme de arttı. Elde edilen kümeyi vir(D) olarak işaretledik. vir(D)’nin yaklaşık 15X1011 noktadan ibaret olduğu görüldü.
“a hanedan vektörünü” Rk’da vir(D) kümesi üzerinden geçen rastlantısal vektör olarak kabul edelim. Bu durumda, vir(D) kümesi üzerinde z olasılıklar yoğunluğu fonksiyonunu kurabiliriz. Bunun için, bütün R15 uzayı yeterince küçük boyutlu standart küplere, vir(D) kümesinin hiçbir noktası bir küpün sınırına düşmeyecek şekilde bölündü. x küpün iç noktası ise, o halde:
| z(x) = | vir(D) kümesinin küpe düşen noktalarının miktarı |
| vir(D) kümesindeki noktaların genel miktarı |
Açıktır ki, bir küpün sınırında bulunan bir x noktası için z(x)=0 sayılabilir. z(x) fonksiyonu vir(D) kümesinden çok sayıda hanedanın bulunduğu bölgede maksimuma ulaşır ve vir(D) kümesinin noktalarının olmadığı bölgede sıfıra düşer, res.5.19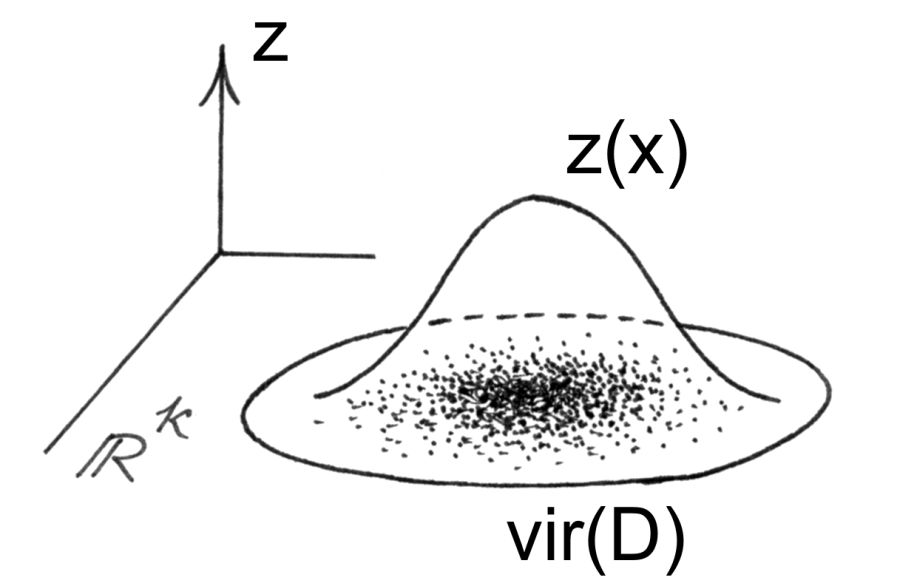
. Böylelikle, z(x) fonksiyonunun grafiği sanal vir(D) hanedanlarının kümesinin Rk uzayında tam olarak nasıl dağıldığını görsel olarak gösteriyor. Bir başka ifadeyle, bu kümenin hangi yerlerde “yoğun”
ve “gür”; hangi yerlerde seyrek olduğunu gösteriyor.
Şimdi şu iki hanedanı ele alalım.
a=(a1,...ak) ve b=(b1,...,bk)
Bunların ne kadar uzak ya da ne kadar yakın olduğunu değerlendirmek istiyoruz.
Merkezi a noktasında bulunan, köşegeninin yarısı a-b vektörü olan k boyutlu P'(a,b) paralelyüzünü oluşturalım, res.5.20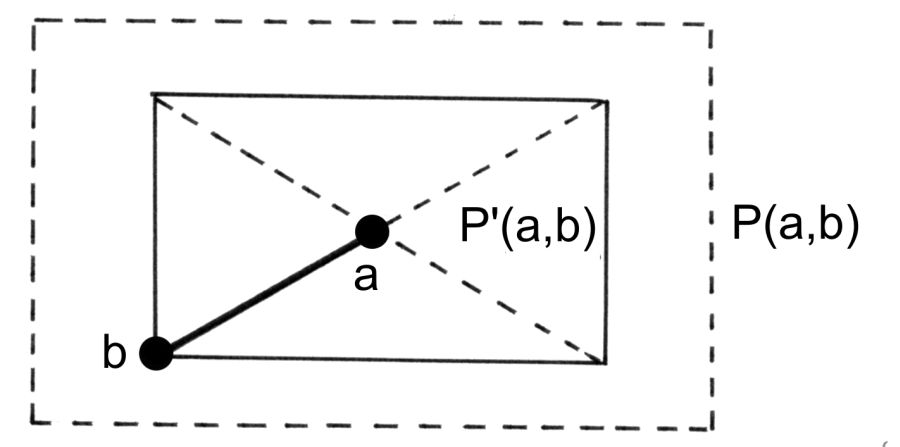
. P'(a,b) paralelyüzünü i koordinat eksenine yansıtırsak [ai - |ai - bi|, ai + |ai - bi|] uçlu dilimi elde edeceğiz.
c'(a,b) Hazırlık katsayısı olarak şu sayıyı alacağız:
| c'(a,b) = | P'(a,b)’e düşen vir(D) kümesinin noktalarının miktarı ------------------------------------------------------------------------- |
| vir(D) kümesindeki noktaların genel miktarı |
Açıktır ki, c'(a,b) sayısı P'(a,b) paralelyüzü üzerinde z(x) yoğunluk fonksiyonunun
integralidir.
Bu c'(a,b) hazırlık katsayısının anlamı açıktır. P'(a,b) paralelyüzüne düşen hanedanlarının, yani vir(D)’nin vektörlerinin, en az b kadar a hanedanına “benzer” olduğunu söylemek doğaldır. Gerçekte de böyle hanedanların her birisi a hanedanına, b hanedanının a hanedanına uzak olduğu kadar, uzak değildir. Buna göre, a ve b hanedanlarının yakınlık ölçüsü olarak, vir(D) kümesinde en az b kadar a hanedanına benzer hanedanların sayısını alıyoruz.
Ancak bu c'(a,b) katsayısı henüz yeteri kadar tatmin edici değildir, çünkü vakanüvüslerin hükümdarların iktidar yıllarını hatalı olarak saptadığını, hem de bu hatanın iktidar yılları ne kadar uzunsa genellikle o kadar büyük olduğunu hiç hesaba katmıyor. Başka bir deyişle, vakanüvislerin yukarıda betimlediğimiz üçüncü yanlışlığını dikkate almamız gerekiyor.
Üçüncü yanlışlığın modellenmesine geçelim. Diyelim ki T iktidar süresidir. Açıktır ki, iktidar süresi “bütün hükümdarların kümesi üzerinde” saptanmış rastlantısal bir değer olarak algılanabilir. T senedir hüküm süren hükümdarların miktarını g(T) olarak gösterelim. Bu kitabın yazarı, J. Blair’in “Kronolojik Tabloları”nda bulunan veriler üzerinde, g(T) frakanslarının histogramını (kaydedilen rastlantısal ölçünün dağılım yoğunluğunu) [884] yapıtında hesaplamıştır. Diyelim ki, h(T)=1/g(T). Burada h(T) vakanüvislerin hatalarının fonksiyonudur. Rastlantısal değer -yani iktidar süresi - T değerini ne kadar az olasılıkla üstleniyorsa, T uzunluğunun hesaplanmasında h(T) yanlışlığı o kadar büyüktür. Başka bir deyişle, hükümdarların küçük, “kısa” iktidar süreleri vakanüvisler tarafından daha iyi hesaplanıyor. Burada vakanüvis çok yanılmıyor. Aksine, hükümdarların seyrek rastlanan uzun iktidar sürelerini ise çok hatalı hesaplıyor. İktidar süresi ne kadar uzunsa, olası hata o kadar büyük oluyor.
Rastlantısal değerin (iktidar süresinin) kaydedilen olasılıklar yoğunluğunun h(T) yanlışlıklar fonksiyonu deneysel olarak çıkarılmıştır, [884], s.115. T tamsayısal ekseninin [0,100] dilimini aynı uzunluğa sahip on dilime bölelim. Bunlar [0,9], [10,19], [20,29], [30,39], ... [90,99]. Öyle görünüyor ki,
T, 0 ila 19 arasında dalgalanıyorsa, h(T)=2,
T, 20 ila 29 arasında dalgalanıyorsa, h(T)=3,
T, 30 ila 99 arasında dalgalanıyorsa, h(T)=5([T/10]-1).
Burada [s] olarak s sayısının tam kısmı gösterilmiştir, res.5.21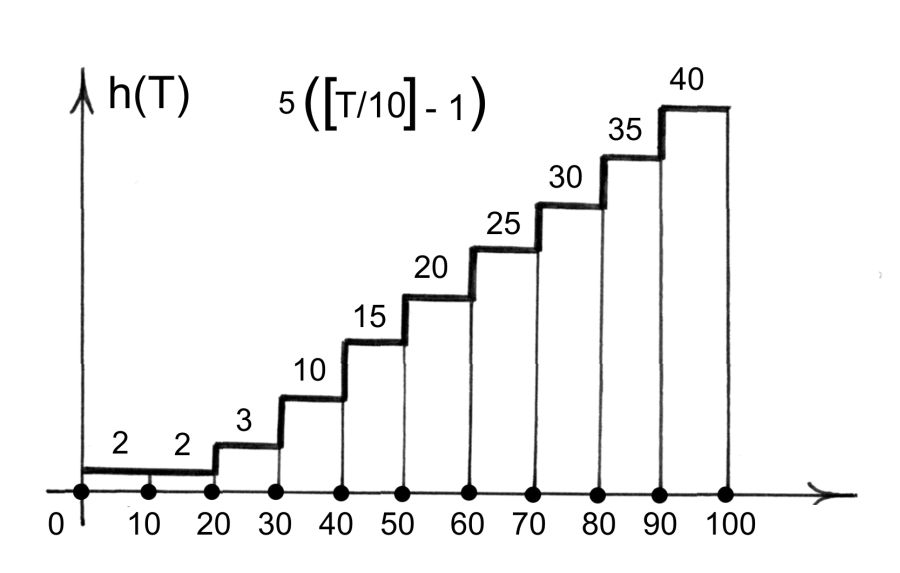
.
Şimdi, vakanüvislerin a noktasının “çevresinin” kurulmasında yaptıkları hataları hesaba katalım. Bunun için P'(a,b) paralelyüzünü merkezi yine a noktası olan, koordinat eksenindeki ortogonal izdüşümü
[ai - |ai - bi| - h(ai), ai + |ai - bi| + h(ai)].
uçlu dilimler olan daha büyük P(a,b) parelelyüzüne kadar genişletelim.
P'(a,b) paralelyüzünün tümüyle P(a,b) paralelyüzünün içinde yer aldığı ortadadır, res.5.20. Bu büyük paralelyüzün köşegeninin yarısı, a-b+h(a)vektörüdür. h(a) ise şudur:
h(a)=(h(a1),...,h(ak))
Bunu vakanüvislerin yanlışlıklarının vektörü olarak adlandırabiliriz.
Böylelikle vakanüvislerin hükümdarların iktidar yıllarının hesaplanmasında yaptıkları üç ana yanlışlığı modellemiş olduk. a ve b hanedanlarının birbirine yakınlığını ve uzaklığını ölçen kesin c(a,b) katsayısı olarak şu sayıyı vereceğiz:
| c(a,b)= | P(a,b)’ye düşen vir(D) kümesinin noktalarının miktarı ------------------------------------------------------------------------ |
| vir(D) kümesindeki noktaların genel miktarı |
c(a,b) sayısının P(a,b) paralelyüzü üzerinde z(x) yoğunluk fonksiyonunun integrali olduğu açıktır. Res.2.22’de
c(a,b) sayısı, tabanı P(a,b) parallelyüzü olan ve yukarıdan z fonksiyonunun grafiği ile sınırlı prizma hacmi olarak gösteriliyor. İstenirse, c(a,b) sayısı, h(a) yanlışlığı göz önünde bulundurularak, z yoğunluk fonksiyonu ile Rk uzayında dağılan rastlantısal “hanedan vektörünün” a noktasına, a ve b noktaları arasındaki “mesafeyi” aşmayan uzaklıkta bulunması olasılığı olarak yorumlanabilir. Bir başka ifadeyle, z yoğunluk fonksiyonu ile dağılan rastlantısal “hanedan vektörü”, “yarıçapı” a-b+h(a) olan a noktasının P(a,b) çevresine düşmüştür.
Yukarıda kaydedildiği gibi, a ve b hanedanlarının c(a,b) katsayısının hesaplanmasındaki rolü aynı değildir. A hanedanı P(a,b) paralelyüzünün merkezinde bulunurken b hanedanı köşegenini belirledi. Elbette önceki p(X,Y) katsayısına örnekseme yoluyla, a ve b hanedanlarına birbiriyle “eşit hak” sağlamak mümkündü. Yani a ve b hanedanlarının yerlerini değiştirip c(a,b) katsayısını hesapladıktan sonra c(a,b) ve c(b,a) sayılarının aritmetik ortalamasını çıkarmak mümkündür. Biz bunu iki sebeple yapmadık. Birincisi, somut deneylerin gösterdiği gibi, c(a,b) katsayısının 1/2 (с(a,b)+c(b,a)) katsayısının yerine geçmesi elde edilmiş sonuçları fiilen değiştirmiyor. İkincisi, a ve b hanedanları bazı durumlarda gerçekten eşit olmayabilir, yani onlardan birisi orijinal, diğeri ise yalnız bunun çifti, hayalet yansıması olabilir. Bu durumda, paralelyüzün merkezine orijinallik iddiası olan a hanedanını yerleştirip b “hayalet yansımasını” a hanedanının “tedirginliği” olarak kabul etmek doğaldır. c(a,b) ile c(b,a) arasında ortaya çıkan farklılıklar büyük değildir ve henüz yapmadığımız sonraki daha ince araştırmalarda kullanılmak üzere faydalı malzeme olabilir.
2.3. Modelin Ve Yürütülen Hesaplama Deneyinin Netleştirilmesi
Yukarıda formüle edilen küçük tahrifatlar ilkesi c(a,b) katsayısı üzerinde denetlenmiştir.
1) Denetleme için J. Blair’in Skaliger versiyonu çerçevesinde güya M.Ö. 4000 senesinden M.S. 1800 senesine kadar Avrupa, Akdeniz bölgesi, Orta Doğu, Mısır ve Asya’nın tarihinden hemen hemen bütün kronolojik verileri içeren kronolojik tablolarını [76] kullandık. Daha sonra bu verilere hem Orta Çağ’a ait hem de çağdaş diğer kaynak ve monografilerden aldığımız hükümdarların isimlerini ve onların iktidar yıllarını içeren listeleri ekledik. Kitaplar şunlar idi: C. Bemont, G. Monod [64], E. Bickerman [72], H. Brugsch [99], A.A. Vasilyev [120], F. Gregorovius [195], [196], J. Assad [240], C. Diehl [247], Kohlrausch [415], S.G. Lozinskiy [492], B. Niese [579], V.S. Sergeyev [766], [767], Chronologie Egiptienne [1069], F.K. Ginzel [1155], L. Ideler [1205], L`art de verifier les dates faites historiques [1236], T. Mommsen [1275], Isaac Newton [1298], D. Petavius [1337], I. Scaliger [1387].
2) Daha önce kaydettiğimiz gibi, hanedan sözcüğü ile, unvanlarını ve akraba bağlantılarını dikkate almadan, ülkenin fiili hükümdarlarının sırasını kastediyoruz. Bundan sonra onları kısaca hükümdar olarak adlandıracağız.
3) Ortak hükümdarlar bulunduğu için, bazen onları sıraya sokmakla ilgili olarak sıkıntılar ortaya çıkıyor. En basit kararı aldık: Bunları iktidar yıllarının ortasına göre sıralamak.
4) Belirli bir devletin bütün tarihi boyunca bütün hükümdarlarının sürelerini yansıtan sayı dizisini (dizinin uzunluğu sınırlı değil) HANEDAN AKIMI olarak adlandıracağız. Şu ya da bu hükümdarın çıkarılmasıyla oluşan altdizileri HANEDAN ŞERİDİ olarak adlandıracağız. Her “şerit” monoton olmalı, yani iktidar yıllarının ortalarının monoton şekilde artması lazım. Bunun dışında hanedan şeridinin tam olması, yani atlamasız ve kesiksiz olarak bu akımda yer alan bütün tarihî dönemleri kaplaması lazım. İktidar sürelerinin kaplanmasına meydan bırakılıyor.
5) Gerçek durumlarda, anlaşılabilir sebepler yüzünden, yukarıda kaydedilen gereklilikler belli ölçüde bozulabilir. Örneğin vakanüvisin anlatımından bir sene ya da hükümdarsız dönemin birkaç senesi kaybolabilir. Bu yüzden, küçük boşlukları kabul etmeye mecburuz. Yalnızca uzunluğu bir seneyi aşmayan boşluklara yer verdik. Ayrıca, hanedan akımlarının ve şeritlerinin analizi yapılırken, gerçek tablonun vakanüvislerin yaptıkları (1), (2), (3) yanlışlıkları yüzünden çarpıtılması olasılığını sürekli dikkate almak zorundayız.
6) Net formel tablonun bozulmasının bir sebebi daha vardır. O da, hükümdarın iktidarının süresinin başlangıcını kesin olarak saptamanın zaman zaman zor olmasıdır. Örneğin, başlangıç olarak neyi saymak lazım, hükümdarın fiilen iktidara geldiği ânı mı, tahta
çıktığı ânı mı? II. Friedrich’in hükümdarlığının başlangıcı olarak farklı kaynaklarda farklı veriler bulunmaktadır: 1196, 1212, 1215, 1220 seneleri. Aynı zamanda, hükümdarlığın sonları ile ilgili olarak genellikle hiç sıkıntı olmuyor. Böylece hükümdarın “ikiye ayrılması”, hatta üç alternatifli olarak ele alınması zorunluluğuna varıyoruz. Neyse ki, daha çok sayıdaki alternatifler son derece seyrektir. Bütün bu seçenekler ortak hanedan akımına katılırdı. Bu sırada, araştırmalarda yer almak üzere ayrılan hiçbir hanedan şeridinin hükümdarın aynı iktidar yıllarının iki farklı seçeneğini içermemesi gerekliydi.
7) Skaliger versiyonu çerçevesinde topladığımız kronolojik veriler temelinde, yukarıda sayılan bütün coğrafi bölgeler için 15 uzunluğundaki bütün vakayiname hanedanlarının tam D listesi oluşturulmuştur. Yani art arda gelen 15 hükümdardan ibaret olan bütün hanedanların listesi oluşturulmuştur. Bunun yanında, her hükümdar birkaç onbeş hükümdarlı hanedana girebilir, yani hanedanlar “çakışabilir”. İstatistiksel deneyden geçirilen ana hanedan akımları şunlardır: Roma piskoposları ve papaları, Bizans patrikleri, sarazenler, Yahudi baş kâhinleri, Yunan Baktriyalılar, Ravenne ekşarjları, Mısır firavun hanedanları, Orta Çağ Mısır hanedanları, Bizans hanedanları, Roma İmparatorluğu’nun hanedanları, İspanya, Rusya, Fransa, İtalya, Osmanlı=Ottoman İmparatorluğu, İskoçya, Lacedaemon, Almanya, İsveç, Danimarka, İsrail, Yahudiya, Babil, Suriye, Portekiz, Parfiya, Bosporus İmparatorluğu, Makedonya, Polonya, İngiltere’nin hanedanları.
8) Vakayiname hanedanlarının D listesine (1), (2) “tedirginlikleri” uygulandıktan sonra anlaşıldı ki, yaklaşık 15x1011 sanal hanedan elde ediliyor. Yani, vir(D) kümesinde yaklaşık 15x1011 nokta oluşuyor.
2.4. Deneyin Sonucu: c(a,b) Katsayısı Bağımlı Ve Bağımsız Hanedanlar Arasında Net Bir Ayrım Yapıyor
1977-1979 senelerinde M. Zamaletdinov ve P. Puçkov ile birlikte yaptığımız hesaplama deneyi küçük tahrifat ilkesini doğrulamıştır. Yani, açıkça bağımlı a ve b vakayiname hanedanları için HRKO = c(a,b) katsayısının 10-8 sayısını aşmayıp 10-12 ile 10-10 arasında dalgalandığı anlaşılmıştır. Olasılık yorumu altında, iki bağımlı vakayiname hanedanının incelenen yakınlığı rastlantısal bir olay olarak kabul edilirse, bunun olasılığının az olması, yüz milyarda bir ihtimal gerçekleştiği için, olayın son derece seyrek olması demektir.
Belli olmuştur ki, a ve b hanedanı iki açıkça farklı gerçek hanedanı betimliyorsa, HRKO = c(a,b) katsayısı “çok daha büyüktür”. Daha doğrusu, 10-3 sayısından az değildir ya da “büyüktür”. p(X,Y) katsayısı örneğindeki gibi, burada da HRKO = c(a,b) katsayısının mutlak değerleri değil, “bağımlı zon” ile “bağımsız zon” arasındaki birkaç büyüklük sırasını içeren fark önemlidir, bkz. res.5.23
.
Böylelikle, HRKO katsayısı yardımıyla, açıkça bağımlı ve açıkça bağımsız vakayiname hanedanları arasındaki esaslı farklılığı keşfetmeyi başardık.
2.5. Hükümdar Hanedanlarının Tarihlenmesi Yöntemi Ve Hayalet Hanedan Çiftlerinin Bulunması Yöntemi
Böylece c(a,b) katsayısı yardımıyla bağımlı ve bağımsız hanedan çiftleri gayet güvenilir bir şekilde seçilebilir. Önemli deneysel olgu şudur ki, vakanüvisler “fazla” yanılmıyorlar. Onların yanlışlıkları bağımsız hanedanları ayıran değerden çok daha küçüktür.
Bu, yürütülen deney çerçevesinde, bağımlı vakayiname hanedanlarının seçilmesi ve bilinmeyen hanedanların tarihlenmesi için yeni bir yöntem sunmayı mümkün kılıyor. Yukarıdaki maddenin örneksemesi yoluyla, bilinmeyen d hanedanı için c(a,d) katsayısını hesaplıyoruz. Burada a bilinen tarihlenmiş hanedanlardır. Farz edelim ki, c(a,d) katsayısı küçük olan, yani 10-8 sayısını aşmayan a hanedanını keşfettik. Bu bize a ve d hanedanlarının 1-с(a,d) olasılık ile bağımlı olduğunu iddia etme hakkı veriyor. Yani a ve d hanedanları olasılıkla tarihlerini bilmiş olduğumuz bir gerçek M hanedanına uygun. Böylece a vakayiname hanedanını tarihliyoruz.
Bu yöntemler tarihleri bilinmekte olan Orta Çağ hanedanları üzerinde denetlenmiştir. Yöntemlerin etkinliği tümüyle doğrulanmıştır [904], [908].
Aynı yöntemler “Skaliger tarih ders kitabında” hayalet çiftleri bulmayı mümkün kılıyor. Yani c(a,b) katsayısı 10-8 sayısını aşmayan a ve b vakayiname hanedanları bulacaksak, önümüzde aynı gerçek M hanedanının iki sureti, iki versiyonu bulunduğunu varsayabiliriz. Bu hanedanın, vakayinamelerin sayfalarında çoğalıp “Skaliger ders kitabının” farklı bölümlerine yerleştirildiğini varsaymak doğaldır.
Tekrar vurgulayalım ki, hanedanların “benzerliğine” ya da tersine “benzemezliğine”
atıfta bulunan herhangi bir sonuç ya da varsayım bizim yaptıklarımıza benzer geniş hesaplama deneylerine dayalı olduğu takdirde makul sayılabilir. Aksi takdirde, tartışılmaya layık olmayan bulanık öznel fikirler ön plana çıkıyor.
