CAPITOLO 1
Alcune informazioni necessarie sull’astronomia e la storia dell’astronomia
1. L’eclittica. L’equatore. La precessione.
Prendiamo in considerazione il moto della Terra lungo la sua orbita solare. Di solito si pensa che non sia la Terra stessa a ruotare intorno al Sole, ma piuttosto il centro di massa (centro di gravità) del sistema Terra - Luna, il cosiddetto baricentro. Rispetto alla distanza tra la Terra e il Sole, il baricentro è relativamente vicino al centro della Terra. Le condizioni del presente lavoro ci consentono di considerare il moto orbitale del baricentro attorno al Sole, come identico al moto orbitale della Terra stessa.
Le perturbazioni gravitazionali provocate dai pianeti causano la costante rotazione del piano orbitale del baricentro. Questa rotazione contiene un certo composto sinusoidale primario con altissima periodicità. È integrato da alcune fluttuazioni variabili minori, che ignoreremo. Questo piano orbitale rotante della Terra viene chiamato piano dell’eclittica.
A volte il termine “eclittica” è usato per riferirsi alla circonferenza nella quale il piano dell’eclittica attraversa la sfera immaginaria delle stelle immobili. Supponiamo che il centro di questa sfera coincida con il centro della Terra che si trova sul piano dell’eclittica. Nella Figura. 1.1 viene indicato con il punto O. Non possiamo ignorare il moto della Terra in relazione alle stelle distanti e considerarlo il centro immobile della sfera stellare. I nostri ulteriori riferimenti agli oggetti celesti come il Sole, le stelle ecc., implicano l'identificazione di detto oggetto con il punto della sua proiezione sopra la sfera delle stelle immobili.
L'eclittica ruota nel tempo, ecco perché è nota come “eclittica mobile”. Per far riferimento alla posizione dell'eclittica mobile in un determinato punto temporale, introduciamo il concetto di eclittica istantanea per un determinato anno o epoca. La concezione e le proprietà dello spin vector istantaneo riguardano la disciplina della meccanica celeste. Le successive eclittiche istantanee fissate in epoche diverse, a volte vengono indicate come le eclittiche fisse di dette epoche. Per esempio, è conveniente far riferimento all'eclittica fissa del 1 gennaio 1900. La posizione dell'eclittica mobile per ogni dato momento può essere specificata in relazione a un'eclittica fissa scelta casualmente.
In meccanica celeste la Terra viene considerata un corpo perfettamente solido. È risaputo che un corpo solido possiede il cosiddetto ellissoide di inerzia, che viene rigidamente definito dai suoi tre semiassi. La rotazione di un corpo solido è caratterizzata dal valore e dall'atteggiamento spaziale del vettore di rotazione ω. Il vettore ω viene talvolta indicato come l'asse istantaneo di rotazione. I semiassi dell'ellissoide di inerzia sono ortogonali e possono quindi essere usati come un sistema di coordinate ortogonali. Pertanto, il vettore ω può essere definito dalle proiezioni di x, y e z sopra gli assi di inerzia. I momenti di inerzia del corpo rispetto a questi assi sono rispettivamente indicati con A, B e C. La rotazione del corpo solido è descritta nelle equazioni dinamiche di Eulero-Poisson:
Aẋ + (C – B)yz = MA
Bẏ + (A – C)xz = MB
Cż + (B – A)xy = MC
Nella parte a destra delle equazioni ci sono le proiezioni del vettore M, note come la coppia esterna in relazione con il centro di massa sugli stessi assi. Il momento M deriva dall'effetto della gravità solare e lunare sulla figura ellissoidale della Terra. La Terra viene generalmente considerata un ellissoide biassiale piuttosto che triassiale, in altre parole un ellissoide di rivoluzione.
La posizione del vettore M in relazione agli assi dell'inerzia cambia rapidamente e questi cambiamenti sono di natura piuttosto complessa; tuttavia, l'applicazione delle teorie moderne del moto lunare e tellurico rende possibile calcolarne l'evoluzione in ogni momento nel tempo con sufficiente precisione. Questo ci consente di risolvere l'equazione di Eulero-Poisson, ossia calcolare l'evoluzione del vettore ω.
Le Tavole del Moto della Terra sui suoi Assi e Attorno al Sole ([1295]) compilate dall'eminente astronomo americano Simon Newcomb, vengono utilizzate per tenere conto di tutte le irregolarità inerenti al moto della Terra.
Lo studio dei casi (le configurazioni dei corpi solidi) in cui le equazioni di Eulero-Poisson possono essere risolte con sufficiente precisione, comprende un'area importante dell'odierna meccanica teorica, della fisica e della geometria.
Prendiamo in considerazione il vettore ω della rotazione istantanea della Terra. Definisce l'asse di rotazione, ovvero l'asse istantaneo di rotazione. I punti in cui attraversa la superficie terrestre sono conosciuti come i poli istantanei della Terra, mentre quelli in cui attraversa la sfera celeste, o sfera delle stelle immobili, sono noti come i poli celesti (nord e sud). Consideriamo il piano ortogonale dell'asse istantaneo di rotazione terrestre che attraversa il centro di massa della Terra. La sua intersezione con la superficie terrestre è conosciuta come l'equatore istantaneo di rotazione della Terra, mentre l'intersezione con la sfera celeste viene indicata come l'effettivo equatore celeste o equinoziale.
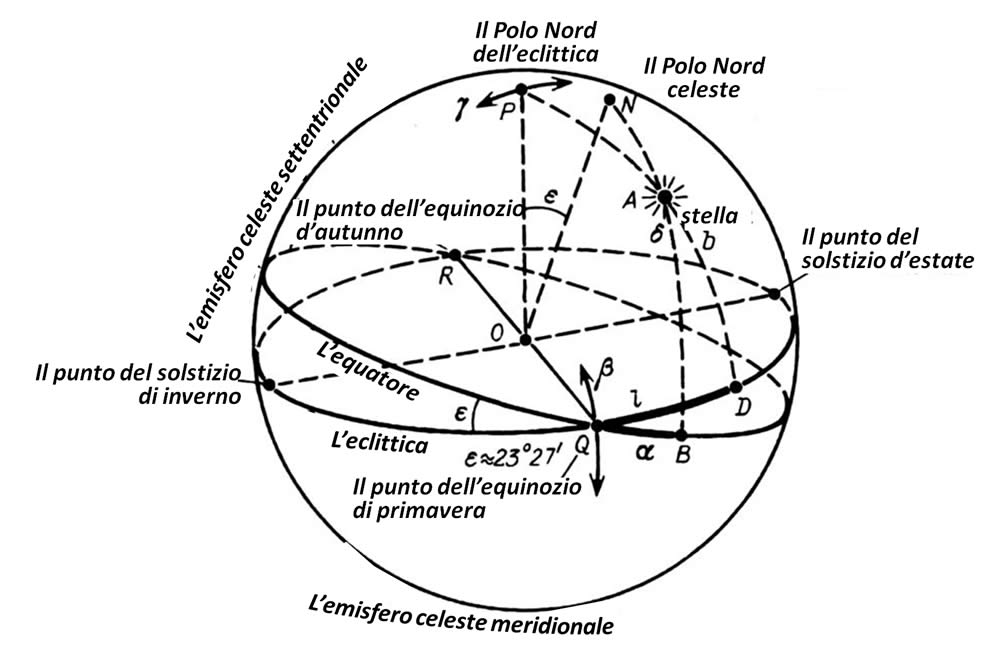
La Figura 1.1 raffigura la sfera celeste. Il suo centro è contrassegnato da OP che sta per Polo Nord dell'eclittica, e da N che è il polo celeste. L'eclittica e l'equatore hanno due punti di intersezione che sono noti come i punti dell'equinozio primaverile e autunnale (indicati rispettivamente nella Figura 1.1 con Q e R). L'illustrazione dimostra anche le alterazioni delle coordinate della stella in relazione ai due sistemi di coordinate della sfera celeste: quello equatoriale e quello dell'eclittica.
Consideriamo ora un sistema di coordinate che non ruota insieme alla Terra, ma che invece si basa sull'eclittica. Il nuovo sistema di coordinate non deve essere ortogonale. Per questi sistemi di coordinate vengono normalmente utilizzati i seguenti assi:
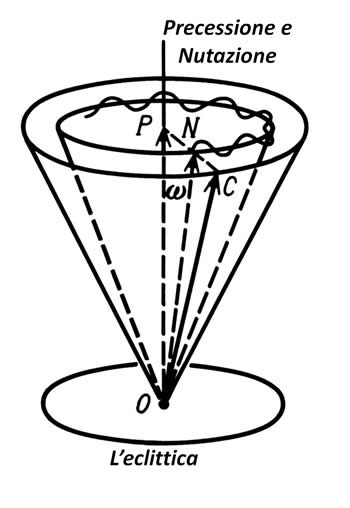
Figura 1.2.
La precessione e la nutazione.
- La normale al piano dell’eclittica;
- l'asse di intersezione dell'eclittica e dei piani equatoriali, o asse equinoziale;
- l’asse C dell’inerzia.
Le proiezioni della velocità angolare istantanea del vettore ω su questi tre assi, sono indicate con ψ,·θ e ϕ. Abbiamo così ampliato la velocità di rotazione terrestre in tre componenti. Qual è il loro significato geometrico? Il valore di ψ è noto come la percentuale di precessione della Terra. Questo componente definisce il moto circolare conico dell'asse C di precessione, ovvero il terzo asse di inerzia, intorno alla normale OP, come mostrato nella Figura 1.2. Il vettore ω = ON segue questa rotazione conica. Vogliamo sottolineare la vicinanza dei vettori ω e OC. Con un calcolo approssimativo possiamo assumere che il vettore ω coincida con l'asse OC.
A causa della precessione, dell'asse equinoziale, o dell'intersezione dell'eclittica e dell'equatore, ruota all'interno del piano eclittico. In una certa misura, la rotazione di θ influisce sull'inclinazione dell'asse OC verso l'eclittica. Infine, il valore di ϕ definisce la velocità della rotazione terrestre attorno all'asse OC. In meccanica teorica il valore di ϕ è noto come la velocità propria di rotazione. È molto superiore alle velocità angolari di ψ e θ. Dal punto di vista della meccanica teorica, questa circostanza riflette il fatto che la rotazione stabile di un corpo solido si manifesta attorno all'asse che sembra essere quello più vicino all'asse del momento massimo di inerzia, ovvero l'asse più corto dell'ellissoide di inerzia. Ricordiamo ai lettori che, in qualche modo, la Terra si appiattisce ai poli.
Pertanto, ω = ψ + θ + ϕ (+ sta per la sommatoria dei vettori). Ogni velocità (ψ, θ e ϕ) contiene un singolo componente costante (o quasi costante) come pure molti altri piccoli periodici comunemente chiamati nutazioni. Se li trascurassimo, rimarremmo con il seguente modello di rotazione terrestre.
- Il componente di velocità costante ψ è chiamato precessione longitudinale. Sposta l'asse OC lungo il cono circolare con la velocità annuale approssimativa di 50" (vedi la Figura. 1.2). L'asse equinoziale si sposta in senso orario lungo l'eclittica, visto dal lato del suo polo nord. Il vettore della precessione è diretto al Polo Sud dell'eclittica.
- A partire da oggi il componente θ di velocità costante è di circa 0,5" all'anno.
- Il componente di velocità costante ϕ è il valore medio della velocità del moto proprio della Terra con la periodicità di un giorno in senso antiorario attorno all'asse AC (visto dal Polo Nord della Terra).
Facciamo notare che l'asse OP, che è la normale verso il piano dell'eclittica, appartiene allo stesso piano del vettore ω, che rappresenta la velocità dell'angolo istantaneo della Terra e l'asse OC, ossia il terzo asse di inerzia. Questo piano ruota attorno all'asse OP a causa della precessione.
I componenti della nutazione inerenti alle velocità (ψ, θ e ϕ) distorcono il modello sopra. Per cui, il vettore ω non segue una traiettoria conica ideale, ma una ondulata e piuttosto irregolare che si avvicina alla forma di un cono. La traiettoria del punto di fine del vettore, nella Figura 1.2 è disegnata come una linea ondulata.
Le due circonferenze che appartengono alla sfera celeste (l'equatore e l'eclittica) si intersecano nell'angolo ε = + 23° 27', in due punti: Q e R, vedi Figura 1.1. Nel corso del suo viaggio annuale lungo l'eclittica, il Sole attraversa due volte l'equatore in questi due punti. Il punto Q, che è dove il Sole entra nell'Emisfero Settentrionale, è il punto dell'equinozio di primavera. Si tratta del punto in cui le durate rispettive del giorno e della notte si equivalgono su tutta la Terra. Il punto R corrisponde all'equinozio di autunno (vedi Figura 1.1).
L'eclittica mobile è in costante rotazione. Perciò,il punto dell’equinozio di primavera si sposta costantemente lungo l'equatore, muovendosi contemporaneamente anche lungo l'eclittica. La velocità alla quale il punto equinoziale viaggia lungo l'eclittica è la precessione longitudinale effettiva. Lo spostamento dei punti equinoziali produce l'effetto di precessione dell'equinozio (vedi Figura 1.1).
2. Le coordinate dell’equatore e dell’eclittica
Per registrare le osservazioni dei corpi celesti, occorre un adeguato sistema di coordinate che consenta di fissare le posizioni rispettive dei corpi celesti. Esistono diversi sistemi di coordinate. Le prime fra tutte sono le coordinate equatoriali, che possono essere definite come segue.
Nella Figura 1.1 possiamo vedere che il Polo Nord è indicato con N, mentre l'equatore celeste contiene l'arco QB. Possiamo stimare che il piano dell'equatore celeste coincide con il piano dell'equatore terrestre, dato che il centro della Terra corrisponde al punto O, che rappresenta il centro della sfera celeste. Il punto Q è il punto dell'equinozio primaverile. Mettiamo che il punto A rappresenti una stella immobile a caso. Prendiamo in considerazione il meridiano NB che attraversa il Polo Nord e la stella A. Il punto B è l'intersezione del meridiano con il piano equatoriale. L'arco QB = α corrisponde alla longitudine equatoriale della stella A. Questa longitudine è anche conosciuta come “ascensione diretta”. La direzione dell'arco è opposta al moto di Q, che è il punto dell'equinozio di primavera. Pertanto, le ascensioni dirette delle stelle raggiungono valori maggiori nel corso del tempo a causa della precessione.
L'arco del meridiano AB = δ corrisponde alla latitudine equatoriale della stella A, che viene anche indicata come la declinazione della stella A. Se volessimo ignorare le fluttuazioni dell'eclittica, le declinazioni delle stelle situate nell'Emisfero Settentrionale diminuirebbero con il tempo a causa del moto dell'equinozio primaverile al punto Q. Le declinazioni delle stelle nell'Emisfero Meridionale con il tempo crescerebbero lentamente.
Il moto quotidiano della Terra non altera le declinazioni delle stelle. Le ascensioni dirette cambiano in modo uniforme e vengono influenzati dalla velocità di rotazione della Terra. La coordinata dell'eclittica è persino piuttosto popolare ed è stata ampiamente utilizzata negli antichi cataloghi stellari.
Consideriamo il meridiano celeste che attraversa il polo eclittico P e la stella A (vedi la Figura 1.1). Attraversa il piano eclittico nel punto D. Nella Figura 1.1 l'arco QD corrisponde alla longitudine dell'eclittica l, mentre l'arco AD rappresenta la latitudine dell'eclittica b. La precessione fa crescere l'arco QD di circa un grado ogni 70 anni, che si traduce nella crescita uniforme delle longitudini dell'eclittica.
Se ignorassimo le fluttuazioni dell'eclittica, potremmo considerare stabili le latitudini b dell'eclittica come prima approssimazione. Questo è proprio il motivo che ha reso così popolari le coordinate dell'eclittica presso gli astronomi medievali. Il vantaggio delle coordinate eclittiche su quelle equatoriali è che il valore di b è costante, mentre il valore di l cresce con il corso di tempo a causa della precessione. Le alterazioni delle coordinate equatoriali causate dalla precessione sono conformi a formule molto più complesse che spiegano la curva ortogonale dell'eclittica che la collega all'equatore.
È proprio per questo motivo che gli astronomi medievali provarono a compilare i loro cataloghi utilizzando le coordinate dell'eclittica, nonostante quelle equatoriali siano più facili da calcolare con le osservazioni, poiché tali calcoli non prevedono la definizione del piano eclittico. La posizione dell'eclittica dipende dal movimento della Terra attorno al Sole e per essere calcolata richiede l'uso di metodi sofisticati che, a loro volta, portano a ulteriori errori sistematici nelle coordinate di tutte le stelle. La scoperta del fatto che nel corso del tempo l'eclittica fluttua, ha portato a usare nei cataloghi le coordinate stellari equatoriali al posto del sistema eclittico. Questo sistema è ancora usato: il “vantaggio” del sistema eclittico appartiene al passato.
3. Il metodo di misura delle coordinate eclittiche ed equatoriali
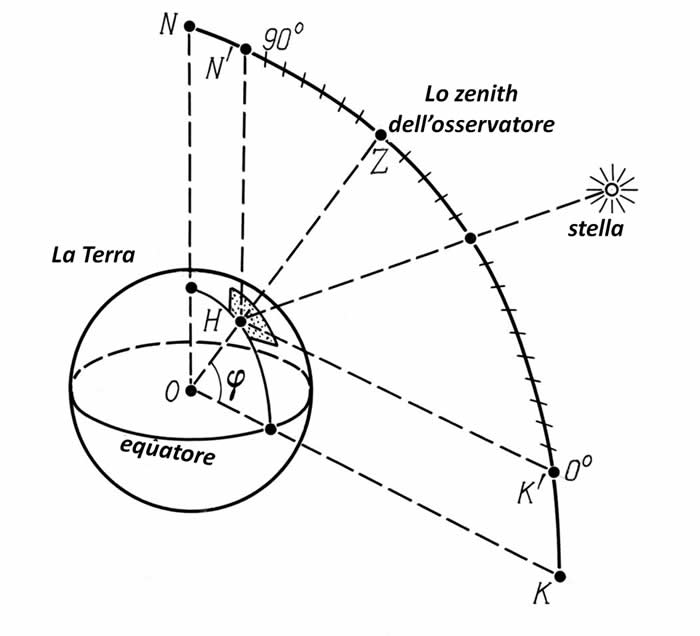
Figura 1.3.
. Il principio di misurazione delle coordinate stellari.
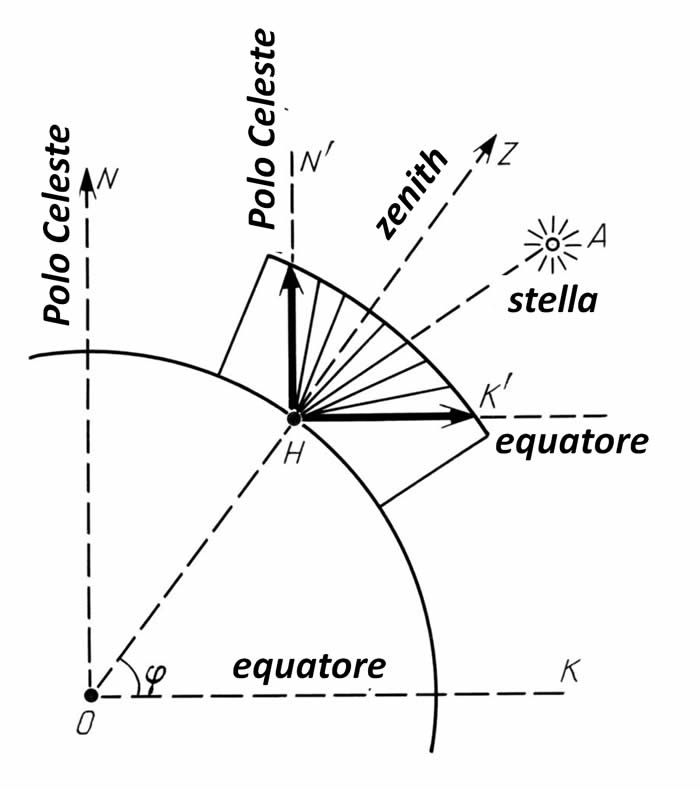
Figura 1.4.
La misura delle coordinate di una stella che passa per un meridiano.
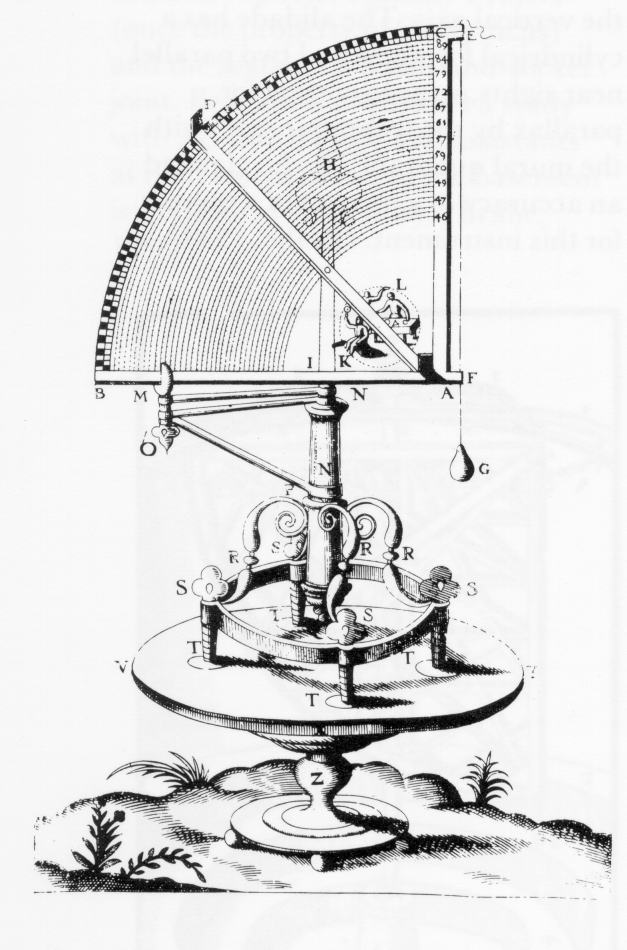
Prendiamo brevemente in considerazione una serie di metodi reali utilizzati per la stima delle coordinate equatoriale ed eclittiche. Descriviamo l'idea geometrica certa che utilizza dispositivi di misura semplici come il sestante, il quadrante e la sfera armillare.
Supponiamo che l'osservatore H si trovi nel punto ϕ sulla superficie della Terra (vedi le Figure 1.3 e 1.4). È piuttosto facile definire la linea HN' che è orientata al Polo Nord celeste e la linea parallela ON. In seguito dobbiamo definire il meridiano che attraversa il punto H e montare una parete verticale sulla superficie terrestre che percorrerà questo meridiano, vedi le Figure 1.3 e 1.4. Segnando con HN' la direzione del polo celeste sulla parete, possiamo anche indicare l'equatore con HK', che è parallelo a OK, dopo aver ricavato l'angolo ![]() dalla direzione HN'. L'angolo retto N'HK' può essere diviso in gradi, fornendoci così lo strumento astronomico per le misurazioni angolari, la parte del cerchio diviso posizionata verticalmente.
dalla direzione HN'. L'angolo retto N'HK' può essere diviso in gradi, fornendoci così lo strumento astronomico per le misurazioni angolari, la parte del cerchio diviso posizionata verticalmente.
Anche gli strumenti moderni si basano su questo strumento; può essere utilizzato per misurare le declinazioni delle stelle o le loro latitudini equatoriali, come pure per segnare i momenti in cui le stelle attraversano un dato meridiano, la cosiddetta verticale.
Una serie di misurazioni consecutive indipendenti rende possibile stimare, con precisione sufficientemente alta, il piano equatoriale per la latitudine dell'osservazione. Allo stesso tempo, come è ovvio da quanto detto sulla meccanica celeste elementare, con la misurazione delle longitudini si devono fissare i momenti in cui le stelle attraversano il meridiano. Per fare questo occorre un cronometro sufficientemente preciso o un dispositivo ausiliario che fornisca misurazioni veloci delle distanze longitudinali tra la stella che ci interessa e un meridiano fisso. Ad ogni modo, le misurazioni longitudinali sono un'operazione sostanzialmente più delicata. Pertanto dovremo aspettarci che le misurazioni delle ascensioni dirette condotte dagli astronomi medievali siano più grossolane che quelle delle declinazioni.
Al fine di misurare le coordinate eclittiche delle stesse, l'osservatore H deve prima valutare la posizione celeste dell'eclittica. Questa operazione è abbastanza sofisticata e prevede una buona comprensione degli elementi primari del moto solare e tellurico. Gli antichi metodi di misurazione dell'angolo di declinazione tra l'eclittica e l'equatore, come pure la posizione dell'asse equinoziale con l'aiuto della sfera armillare o astrolabio, sono descritti in [614] e in moltissime altre fonti. Va notato che per misurare le coordinate eclittiche di una serie di stelle c'è bisogno di un qualche tipo di dispositivo di cronometraggio, al fine di compensare la rotazione giornaliera della Terra e mantenere l'orientamento nel punto costante dell'equinozio.
L'ovvia complessità di questo compito portò a quanto segue: per calcolare effettivamente le coordinate dell'eclittica, gli astronomi potevano usare sia la formula di rotazione della sfera celeste, che i globi celesti con le griglie delle coordinate equatoriali ed eclittiche. La conoscenza delle coordinate equatoriali consentiva di calcolare le equivalenti coordinate eclittiche. Ovviamente, c'erano degli inevitabili errori derivanti dalla mancanza di sufficiente precisione nella stima delle posizioni comparative dell'eclittica e dell'equatore, come pure la posizione dell'asse equinoziale.
Questa discussione molto concisa sui metodi utilizzati per la misurazione delle coordinate eclittiche, ci consente di dire che molto probabilmente gli astronomi medievali utilizzavano il seguente algoritmo:
- Calcolavano le coordinate equatoriali e le misure latitudinali erano più precise rispetto alle longitudinali.
- In seguito stimavano la posizione dell'eclittica e l'asse equinoziale in relazione all'equatore.
- Infine dovevano convertire le coordinate equatoriali nelle equivalenti eclittiche con l'aiuto di strumenti speciali di misurazione o formule trigonometriche (oppure, in alternativa, mediante l'uso di un globo celeste dotato di una griglia a doppia coordinata).
Inoltre, dal momento che tutti gli antichi strumenti di misurazione venivano inevitabilmente installati sulla superficie terrestre, l'algoritmo sopracitato è l'unico vero metodo di calcolo delle coordinate stellari dell'eclittica. Dal momento che gli strumenti di misura installati sulla superficie della Terra partecipano alla rotazione quotidiana del pianeta, gli strumenti in questione sono inevitabilmente legati al sistema delle coordinate equatoriali.
L'applicazione dei nostri metodi statistici ai dati forniti dal catalogo dell'Almagesto ha confermato l'utilizzo dell'algoritmo di cui sopra, come dimostreremo di seguito.
4. La moderna sfera celeste
Per poter datare un vecchio catalogo stellare tramite i valori numerici delle coordinate stellari ivi contenute, dobbiamo essere in grado di calcolare le posizioni delle stelle sulla sfera celeste per i vari punti temporali del passato. Le informazioni che utilizziamo come riferimento sono le descrizioni esistenti della sfera celeste nel suo stato odierno. Gli unici dati importanti sono le coordinate stellari, come pure la loro magnitudine e il valore del moto proprio.
Anticipando, possiamo far notare che il metodo di datazione che suggeriamo è applicabile solo se le rispettive posizioni delle stelle cambiano con il corso del tempo. La rotazione dell'intera sfera celeste risultante dalla transizione verso un altro sistema di coordinate, non può essere utilizzata per scopi indipendenti di datazione. Ne parleremo più dettagliatamente di seguito.
Parliamo delle caratteristiche delle stelle a cui faremo riferimento nella nostra ricerca.
In un catalogo moderno la magnitudine della stella è il numero che rappresenta la sua luminosità. Più basso è il valore, più luminosa è la stella. C'è una vecchia tradizione che indica detti valori nei cataloghi stellari. L'Almagesto contiene i valori di magnitudine di tutte le stelle elencate. Le stelle più luminose vengono indicate come stelle di prima magnitudine, quelle meno luminose corrispondono alla seconda magnitudine e così via. I cataloghi moderni usano la stessa scala per riferirsi alla luminosità di una data stella. Tuttavia, le magnitudini stellari possono anche essere espresse con delle frazioni. Per esempio, Arturo, che nell'Almagesto possiede una magnitudine pari a 1, nel moderno The Bright Star Catalogue ([1197]) è apri a 0.24. Anche Sirio nell'Almagesto è una stella di magnitudine 1, mentre nel catalogo moderno è pari a -1.6. Per cui Sirio è più luminosa di Arturo, sebbene Tolomeo credesse che fossero equamente splendenti.
La questione potrebbe essere che, nell'antichità, la luminosità (o magnitudine) di una stella veniva stimata dall'osservatore in modo molto approssimativo. Oggi la magnitudine stellare viene stimata con il metodo fotometrico. Il confronto tra le magnitudini stellari contenute nell'Almagesto con i loro precisi valori moderni, che è stato indicato nell'opera di Peters e Knobel ([1339]), dimostra che la discrepanza di solito non supera 1 o 2 unità di misura.
Nei nostri calcoli sulle posizioni effettive delle stelle nel passato, ci siamo riferiti principalmente al The Bright Star Catalogue ([1197]), che contiene le caratteristiche di circa 9000 stelle e arriva fino all'ottava magnitudine stellare. Ricordiamo ai lettori che a occhio nudo è possibile vedere solo le stelle di magnitudine 6 o 7. Secondo le affermazioni di Tolomeo, il catalogo stellare dell'Almagesto contiene tutte le stelle della parte visibile del cielo che arrivano fino alla sesta magnitudine.
Tolomeo stava esagerando: ci sono più stelle di magnitudine 6 e meno nella parte visibile del cielo che nel catalogo dell'Almagesto. Questo è uno dei motivi per cui i tentativi di identificare le stelle dell'Almagesto con le posizioni stellari calcolate “al contrario” conducono solo a delle ambiguità (per maggiori dettagli vedere il Capitolo 2). D'altra parte, sarebbe naturale supporre che tutte le stelle che furono effettivamente osservate da Tolomeo o dai suoi predecessori esistano ancora e possano essere trovate anche in un catalogo moderno ([1197]).
J. Bayer, prominente astronomo del XVII secolo, suggerì un nuovo sistema di riferimento per le stelle di una costellazione. Suggerì di usare le lettere dell'alfabeto greco al posto di descrivere verbalmente al posizione di una determinata stella in una costellazione. La stella più luminosa della costellazione veniva indicata dalla lettera α, la seconda più luminosa dalla lettera β, e così via. Successivamente, Flamsteed (1646-1720) inventò una numerazione speciale per le stelle di una costellazione; più specificamente, la stella più occidentale della costellazione fu indicizzata con 1, quella a est con 2, e così via. I numeri di Flamsteed e le lettere di Bayer vengono spesso combinate insieme per riferirsi a una stella (32α Leonis e così via). A parte questo, alcune stelle hanno dei nomi individuali. Queste stelle “dotate di nome” sono relativamente rare. I nomi individuali venivano assegnati solo alle stelle che avevano un significato speciale nell'astronomia antica. Per esempio, 32α Leonis si chiama Regolo.
Abbiamo usato le seguenti caratteristiche stellari dal catalogo moderno ([1197]):
- L'ascensione diretta di una stella nell'epoca del 1900, che veniva scritta in basso con α1900, era espressa in ore, minuti e secondi.
- La declinazione di una stella della stessa epoca veniva trascritta con δ1900 ed era misurata in gradi, minuti d'arco e secondi.
- La magnitudine della stella.
- La frequenza del moto proprio di una determinata stella. La frequenza del moto proprio è composta da due elementi: il primo è il tasso di fluttuazione della declinazione della stella, mentre il secondo è il tasso di alterazione della sua ascensione diretta. Tuttavia, la griglia delle coordinate longitudinali e latitudinali posta su una sfera, non è uniforme. Le distanze tra i meridiani adiacenti diminuiscono più ci si avvicina ai poli; perciò, la componente della velocità stellare dell'ascensione diretta ci offre un'idea sbagliata della velocità effettiva, ovvero la velocità “visibile” della stella sulla sfera celeste nella direzione del parallelo. Pertanto, alcuni moderni cataloghi stellari riportano la riduzione all'equatore della velocità stellare dell'ascensione diretta. Ciò significa che il valore viene moltiplicato per il coseno di declinazione, che rende possibile interpretarlo come la lunghezza locale euclidea della proiezione del vettore di velocità stellare sull'equatore (il parallelo). Ciò consente di confrontare le prime componenti della velocità stellare a prescindere dalla loro vicinanza al polo. Se in questo modo le velocità non si riducono, per il confronto servono dei calcoli aggiuntivi.
Tra i cataloghi che abbiamo usato, in BS4 ([1197]) e BS5 (fonte online) le velocità all'equatore si sono ridotte, mentre non è così per i cataloghi FK4 ([1144]) e FK5 (fonte online). Anche se suona abbastanza strano, questo fatto non è sempre menzionato nelle descrizioni dei cataloghi astronomici. La forma delle velocità dell'ascensione diretta devono essere stimate dai loro valori numerici effettivi.
I valori delle frequenze del moto proprio di una stella sono piuttosto piccoli. Normalmente non superano 1" all'anno. Più sono veloci le stelle visibili ad occhio nudo, come ο2 Eri, μ Cas, più la frequenza si sposta verso i 4" all'anno.
Le traiettorie del moto stellare per gli intervalli di tempo che ci interessano (2-3 mila anni) possono essere considerate diritte, il che significa che ciascuna delle coordinate stellari sulla sfera celeste cambia in modo uniforme. Questa approssimazione è valida solo per le aree che si trovano a una certa distanza dal polo, ovviamente abbastanza distanti.
Il sistema standard delle coordinate per la sfera celeste che viene indicato negli odierni cataloghi stellari, si basa abitualmente sulle coordinate equatoriali per le epoche del 1900, 1950 e 2000 d.C. Per l'inizio del 1900 d.C. abbiamo scelto il sistema delle coordinate equatoriali. Gli ulteriori calcoli e conversioni del sistema delle coordinatele per una data epoca t, si sono basati su questo sistema.
Innanzitutto, per poter datare il catalogo dell'Almagesto avremo bisogno delle coordinate delle stelle con frequenze alte di moto proprio. Naturalmente, prenderemo in considerazione solo le stelle veloci che si ritiene siano state elencate nell'Almagesto.
Ci siamo astenuti dal discutere il problema se le stelle dell'Almagesto siano state identificate correttamente o meno. Lo considereremo nei dettagli più avanti. Per poter risolvere il problema dell'identificazione, dobbiamo sapere se nei cataloghi antichi una determinata stella aveva un nome individuale. Le informazioni sui nomi medievali delle stelle sono stati presi dai cataloghi BS4 ([1197]) e BS5 (fonte online).
Per poter datare il catalogo dell'Almagesto attraverso le frequenza del moto proprio, avremo bisogno delle seguenti due liste di stelle dai cataloghi moderni. Dovremo semplicemente includerne la descrizione; le liste effettive sono disponibili in Appendice 1.
Faremo riferimento alla prima lista come l'elenco delle stelle “veloci”. Nella prima fase della compilazione di detta lista abbiamo selezionato tutte le stelle la cui velocità da una delle coordinate sia almeno maggiore di 0,1" all'anno. Questa lista è stata successivamente ridotta alle stelle che contengono una lettera greca di Bayer o il numero di Flamsteed dentro il loro nome. Pertanto, abbiamo rifiutato tutte le stelle che a priori erano inutili per la datazione dell'Almagesto. La questione è che quasi tutte le stelle identificate dagli astronomi come una stella dell'Almagesto, ha un indice nel sistema di Bayer, in quello di Flamsteed o in entrambi; inoltre, se una stella dell'Almagesto è stata identificata come estranea a quegli indici, questa identificazione è sempre piuttosto ambigua ([1339]). Il motivo è abbastanza chiaro. I cataloghi di Bayer e Flamsteed erano già stati compilati nell'epoca delle prime osservazioni telescopiche, ovvero il XVII-XVIII secolo. Se una determinata stella veniva omessa da quei cataloghi, era perché era troppo debole o troppo difficile da distinguere dagli oggetti celesti che si trovavano nelle sue immediate vicinanze.
Potrebbero esserci altre complicazioni dello stesso stile; pertanto, difficilmente si può presumere che una stella di questo tipo possa essere identificata in modo veritiero come una stella dell'Almagesto e che la sua posizione venne misurata con sufficiente precisione dagli astronomi “antichi”.
La selezione di cui sopra ci ha dato una lista di stelle “veloci” e visibili ad occhio nudo, che possono essere trovate nei moderni cataloghi stellari ed essere identificate come stelle dell'Almagesto. E' piuttosto ovvio che la veridicità di tali identificazioni richiede uno studio separato. Considereremo questo problema più avanti.
La nostra lista delle stelle “veloci” e visibili ad occhio nudo, la potete trovare nella Tabella P1.1 dell'Appendice 1.
La seconda lista di stelle è l'elenco delle stelle che hanno un nome. È contenuta nelle Tabelle P1.2 e P1.3. Nella Tabella P1.2 le stelle sono disposte per nome, mentre nella Tabella P1.3 tramite i rispettivi numeri del The Bright Star Catalogue ([1197]). Questo elenco contiene tutte le stelle che hanno un nome individuale secondo BS4 ([1197]), o che avevano quei nomi già nel passato (Arturo, Aldebaran, Sirio, ecc...).
Le liste delle stelle veloci e di quelle con nome si intersecano: una stessa stella può avere sia una frequenza di moto proprio visibile che un nome individuale. Queste stelle sono le più utili per la datazione dell'Almagesto.
5. Il calcolo “inverso” della posizione degli oggetti sulla sfera celeste. La formula di Newcomb-Kinoshita
5.1. Le formule necessarie.
Avendo a nostra disposizione le coordinate moderne e la frequenza di moto proprio delle stelle, possiamo compilare un catalogo stellare sufficientemente preciso per qualsiasi epoca del passato. Con “sufficientemente preciso” intendiamo una precisione che corrisponda alle moderne teorie astronomiche, che è più che sufficiente per i nostri scopi. Tale precisione può essere considerata assoluta in confronto a quella dei vecchi cataloghi.
Abbiamo dovuto eseguire parecchie volte dei calcoli retroattivi sulla posizione della stella nelle diverse epoche. Prima abbiamo calcolato le posizioni delle stelle sulla sfera celeste per l'anno t nelle coordinate α1900 e δ1900, e poi le abbiamo convertite nelle coordinate eclittiche lt e bt per l'epoca t.
Riportiamo le formule necessarie che consentono la conversione delle coordinate αs e δs nelle coordinate ls0 e bs0 per tutte le epoche s e s0. Queste formule tengono conto della precessione e del moto proprio della stella. Dette formule, così come la Figura 1.5 che le illustra, sono state tratte da [1222]. Si basano sulla teoria di Newcomb come modificata da Kinoshita. L'effettiva procedura di conversione delle coordinate viene descritta nella sezione successiva (5.2). In queste formule i momenti temporali s0 e s sono stati conteggiati all'indietro dall'epoca del 2000 d.C usando i secoli giuliani; inoltre θ = s0 - s. Vedi Figura 1.5.
φ(s, s0) |
= 174°52’27,66” + 3289,80023”s0 + 0,576264”s02 - (870,63478” + 0,554988”s0) θ + 0,024578”θ2; |
(1.5.1) |
κ(s, s0) |
= (47,0036” + 0,06639”s0+ 0,000569”s02)θ + (-0,03320” + 0,000569”s0)θ2 + 0,000050”θ3; |
(1.5.2) |
ε0(s, s0) |
= 23°26’21,47” – 46,81559”s0 - 0,000412”s02 + 0,00183”s03 |
(1.5.3) |
ε1(s, s0) |
= ε0(s, s0) + (0,05130” – 0,009203”s0)θ2 – 0,007734” θ3; |
|
ε(s, s0) |
= ε0(s, s0) +(-46,8156” – 0,00082”s00 + 0,005489”s02)θ + (-0,00041” + 0,005490”s0)θ2 + 0,001830”θ3; |
|
ψ(s, s0) |
= (5038,7802” + 0,49254”s0 – 0,000039”s02)θ + (-1,05331” – 0,001513”s0)θ2 – 0,001530”θ3; |
|
χ(s, s0) |
= (10,5567” – 1,88692”s0 – 0,000144”s02)θ + (-2,38191” – 0,001554”s0)θ2 – 0,001661”θ3; |
|
Ψ(s, s0) |
= (5029,0946” + 2,22280”s0 + 0,000264”s02)θ + (1,13157” + 0,000212”s0)θ2 + 0,000102”θ3; |
(1.5.4) |
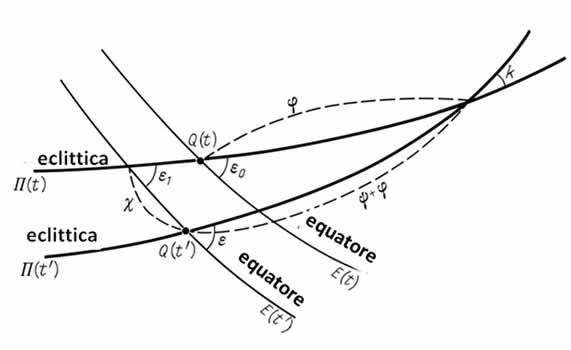
Figura 1.5.
I valori ausiliari per ricalcolare le coordinate stellari tramite il sistema delle coordinate
equatoriali sulla sfera celeste,
corrispondenti all'epoca t' del sistema delle coordinate eclittiche.
Tuttavia, vi facciamo notare che le discrepanze tra i corollari realizzati secondo la teoria effettiva di Newcomb e le sue modifiche apportate da Kinoshita ([1222]) che abbiamo usato, non hanno alcuna conseguenza per quanto riguarda i nostri scopi. Per ogni momento t dell'intervallo storico in esame (tra il 600 a.C. e il 1900 d.C.), le discrepanze tra le coordinate dell'eclittica di una stella calcolata secondo la teoria di Newcomb e quelle ottenute usando la sua versione modificata ([1222]), sono trascurabilmente piccole rispetto agli errori dell'Almagesto. Abbiamo usato [1222], poiché fornisce le formule per la compensazione della precessione in un formato conveniente per i calcoli fatti al computer.
5.2. L'algoritmo per calcolare le posizioni passate delle stelle
Vi forniamo una descrizione dettagliata dell'algoritmo utilizzato per il calcolo del catalogo stellare K(t), che riflette con sufficiente precisione le condizioni della sfera celeste per l'anno t, secondo la teoria di Newcomb. In questo caso, t è un'epoca scelta casualmente dall'intervallo storico in esame (vale a dire quello tra il 600 a.C. e il 1900 d.C.). L'epoca t è stata calcolata a ritroso nel passato dall'epoca del 1900 in anni giuliani; in altre parole, t = 1 corrisponde all'epoca del 1800, t = 10 all'epoca del 900 d.C., t = 18 al 100 d.C., ecc... La discrepanza di alcuni giorni che risulta dalle differenze tra il calendario giuliano e quello gregoriano, e che porta alla situazione in cui l'epoca del 100 d.C., ad esempio, non coincide con l'epoca del 1 gennaio 100 d.C., non è di nessuna importanza.
Il catalogo calcolato K(t) ci servirà per il confronto con il vecchio catalogo in studio (tipo l'Almagesto) con diversi valori di t. Qui t rappresenterà la presunta datazione casuale di un vecchio catalogo. Pertanto, i cataloghi calcolati K(t) dovranno essere iscritti nelle coordinate eclittiche per l'epoca t. Come abbiamo sottolineato, tutti i vecchi cataloghi conosciuti sono stati compilati usando le coordinate eclittiche, sia l'Almagesto di Tolomeo che i cataloghi di Al-Sufi, Ulugbek, Copernico, Tycho Brahe ecc...
Supponiamo che le moderne coordinate equatoriali di un catalogo stellare (tipo [1197]) siano α0 =α01900, δ0 = δ01900. Queste coordinate riflettono la posizione della stella in questione per il 1900 d.C. nel sistema sferico delle coordinate, il cui equatore corrisponde all'equatore terrestre del 1900 d.C. L'equatore viene definito dal piano che è ortogonale all'asse di rotazione della Terra. Ricordiamo ai lettori che la posizione di questo piano cambia nel corso del tempo. Dovremo calcolare le coordinate lt, bt, ossia le coordinate sferiche il cui equatore coincide con l'eclittica, cioè il piano di rotazione della Terra attorno al Sole per l'epoca t. Per questo scopo dovremo fare ciò che segue.
Passaggio 1. Dobbiamo calcolare le coordinate stellari α0(t), δ0(t) per il momento temporale t nel sistema delle coordinate equatoriali per il 1900 d.C. Tenete presente che la posizione delle stelle sulla sfera celeste cambia nel corso del tempo in relazione a qualsiasi sistema fisso di coordinate. I calcoli richiesti per la posizione della stella si basano sulla frequenza del moto proprio vα, vδ della stella per ciascuna delle coordinate α1900, δ1900 (vedi Tabella 4.1, colonne 5 e 6). Per le frequenze non ridotte di moto proprio abbiamo escogitato quanto segue:
α0(t) = α01900(t) = α0 - vαsub>·t,
δ0(t) = δ01900(t) = δ0 - vδsub>·t.
In effetti, possiamo considerare che le frequenze del moto proprio di ogni stella tramite le coordinate α1900, δ1900 sono costanti. Nelle formule citate sopra il segno meno deriva dalla natura retroattiva dei calcoli; i simboli della frequenza di velocità vα, vδ corrispondono al flusso normale del tempo.
Prima di poter usare effettivamente questa formula, dobbiamo convertire tutti i valori originali in un unico sistema di misurazione. Ad esempio, possiamo misurare α0(t) e δ0(t) in radianti e le velocità vα, vδ - in (rad ÷ anno) 10-2.
Passaggio 2. Dobbiamo spostarci dalle coordinate α1900, δ1900 alle coordinate l1900, b1900. Dovremo trovare le coordinate l0(t), b0(t) della nostra stella per il momento t nelle coordinate sferiche basate sull'eclittica per l'epoca del 1900 d.C. Ecco cosa viene fuori:
sin b0(t) = |
-sin α0(t) cos δ0(t) sin ε0 + sin δ0(t) cos ε0 |
|
tan l0(t) = |
sin α0(t) cos δ0(t) sin ε0 + sin δ0(t) cos ε0, cos α0(t) cos δ0(t) |
(1.5.5) |
ε0 = |
23°27’8,26”. |
|
Queste formule consentono l'inequivocabile ricostruzione dei valori di β0(t) e α0(t), dato che –90° <b0(t) <90° e |l0(t) - α0(t)| τ90°. Il valore di ε0 corrisponde all'angolo della declinazione tra l'eclittica del 1900 d.C. e l'equatore del 1900 d.C. Ricordiamo ai lettori la formula di 1.5.3, dove occorre lasciare che s0 = –1 per effettuare la transizione tra il 2000 d.C. e il 1900 d.C.
Figura 1.6.
La sequenza dei passaggi che abbiamo utilizzato per i calcoli inversi
delle posizioni stellari e delle loro coordinate nel passato.
Passaggio 3. Dobbiamo spostarci dalle coordinate l1900, b1900 alle coordinate ausiliarie l1 e b1, che sono anche legate all'eclittica del 1900. Tuttavia, hanno un diverso punto di riferimento longitudinale, che coincide con l'intersezione dell'eclittica del 1900 d.C. e quello dell'epoca t, o Π1900 e Π(t). Questa transizione è conforme alle seguenti formule:
l1(t) = l0(t) – φ,
b1(t) = b0(t)
φ = 173°57’38,436” + 870,0798”t + 0,024578”t2. (1.5.6)
Se ipotizzassimo che s0 = -1 e θ = -t, l'arco ϕ tra il punto di equinozio di primavera del 1900 sull'eclittica Π1900e l'intersezione di Π1900e Π(t) sarebbe conforme alla formula (1.5.1). Quindi l'eclittica Π(s0) nella Figura 1.5 corrisponde all'eclittica Π1900. L'eclittica Π(s) nella Figura 1.5 rappresenta l'eclittica dell'epoca t che ci interessa. In effetti, il tempo t viene contato a ritroso in secoli dal 1900 d.C., mentre la rimanenza di θ = s - s0 viene contata in avanti dall'epoca s0, anche questa in secoli. Dato che abbiamo concordato che s0 = –1, che corrisponde al 1900 d.C. (2000 - 100 = 1900), dobbiamo scegliere θ = –t per fare in modo che l'epoca s = s0 + θ corrisponda all'epoca t sotto esame nella nostra formula (1.5.1).
Passaggio 4. Successivamente dovremo effettuare la transizione dalle coordinate l1, b1 alle coordinate l2 b2. Sono le coordinate sferiche legate all'eclittica Π(t), dovute solo alla scelta del punto di riferimento longitudinale. Nelle coordinate l2, b2 questo punto corrisponde all'intersezione dell'eclittica Π1900 e Π(t). La formula della transizione da l1, b1 a l2, b2 corrisponde alle formula (1.5.5). Al posto di ε0 dovremo prendere l'angolo ε1 tra l'eclittica Π(t) e Π1900:
ε1 = - 47,0706”t – 0,033769”t2– 0,000050”t3.
Questa espressione è derivata dalla formula (1.5.2) dove s = –1 e θ = –t.
Passaggio 5. Infine, dovremo effettuare la transizione dalle coordinate l2, b2 alle coordinate eclittiche lt, bt. Questa transizione è conforme alla seguente formula:
lt = l2 + φ + Ψ, bt = b2,
dove ϕ è definito in (1.5.6) e Ψ è definito dalla formula (1.5.4) con s0 = –1 e θ = –t, per cui
Ψ = –5026.872"t + 1.1314"t2 + 0.0001"t3.
La sequenza dei passaggi 1-5 descritti sopra è illustrata nella Figura 1.6.
Concludiamo sottolineando che tutti i calcoli necessari per la datazione di un determinato catalogo stellare possono essere eseguiti senza tenere conto della teoria di Newcomb-Kinoshita. Parleremo di questo punto più dettagliatamente in seguito. La teoria di Newcomb-Kinoshita viene usato solo per ottenere informazioni aggiuntive riguardante gli errori nella stima del piano dell'eclittica fatta dall'autore del catalogo. Il valore di queste discrepanze è il fattore ausiliario che conferma la correttezza dei nostri corollari. Vedere i Capitoli 6 e 7.
6. L'Astrometria. Gli antichi strumenti del XV-XVII secolo per le misurazioni astronomiche
Nella sezione 3 abbiamo trattato la concezione generale dei dispositivi di misurazione angolare utilizzati in astronomia, che sono importanti per noi poiché ci consentono di stimare con sufficiente precisione la posizione della linea equatoriale sulla sfera celeste.
Supponiamo che la linea visiva dell'osservatore sia diretto lungo la semiretta HK', che si muove lungo la linea dell'equinoziale nella sua rotazione quotidiana, senza qualsiasi tergiversazione. L'atteggiamento della mezza linea HK' dipenderà naturalmente dalla latitudine geografica. Possiamo definire il piano HLM, un quadrante ortogonale parallelo al piano equatoriale, che attraversa la sfera celeste proprio lungo l'equinoziale, vedere la Figura. 1.7. In quel punto della superficie tellurica è quindi possibile costruire un dispositivo fisso, orientato dal meridiano nord-sud, che ci consenta di contrassegnare visivamente l'equatore sulla sfera celeste. Per esempio, che ci permetta delle stime precise delle latitudini stellari equatoriali, durante il loro attraversamento del piano verticale del quadrante. Come abbiamo già sottolineato, la misurazione delle latitudini equatoriali non era di sicuro un compito complicato per un astronomo professionista del XIV-XVI secolo. C'era solamente bisogno della precisione e del tempo sufficiente per eseguire le osservazioni. In particolare, ci si dovrebbe aspettare che un attento osservatore non faccia gravi errori sistematici nella stima delle declinazioni stellari per un determinato anno.
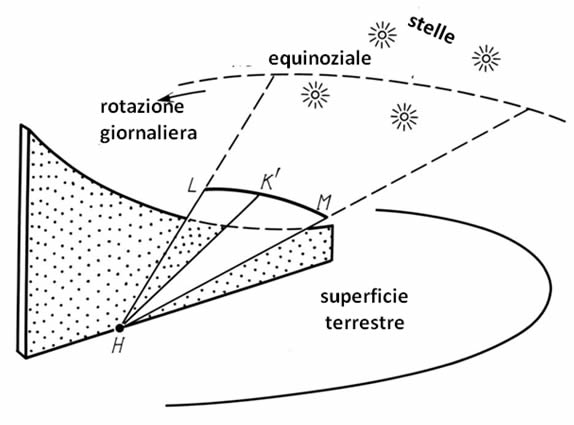
Figura 1.7.
. La misurazione della latitudine delle stelle.

Figura 1.8.
Il circolo meridiano
Ora vediamo in che modo l'idea generale sopra descritta fu implementata in veri e propri strumenti medievali.
Il primo strumento è il circolo meridiano, il cosiddetto strumento dei passaggi descritto da Tolomeo (vedi Figura 1.8). Lo strumento assomiglia a un anello metallico piatto avente un raggio a caso, installato su un supporto affidabile verticalmente al piano del meridiano locale. Lo strumento è graduato (in 360 gradi, per esempio). All'interno dell'anello più grande è posto un altro anello di diametro inferiore; può ruotare liberamente, rimanendo sullo stesso piano dell'anello più grande (Figura 1.8). Ci sono due piccole piastre metalliche con dei puntatori collegati ai due punti opposti dell'anello interno (contrassegnate con P nella Figura 1.8); i puntatori indicano i gradi che si trovano sull'anello esterno. Lo strumento è installato sul piano del meridiano locale con l'aiuto di un livello e della linea meridiana la cui direzione viene definita dall'ombra di un palo verticale a mezzogiorno. Quindi il segno zero sull'anello esterno dello strumento è sincronizzato con lo zenit locale.
È possibile utilizzare lo strumento sopra descritto per misurare l'altezza del sole a una determinata latitudine. A mezzogiorno si deve girare rapidamente l'anello interno fino a quando l'ombra della prima piastra P copre completamente la seconda piastra P. In questo caso, la posizione dei puntatori sulle piastre ci dirà l'altezza del Sole con l'aiuto dei gradi segnati sull'anello esterno. Occorre sottolineare che le indicazioni dello strumento devono essere lette dopo aver fissato le piastre nella giusta posizione. Questo ci dice l'altezza del Sole già dopo mezzogiorno. Inoltre, il circolo meridiano può misurare l'angolo tra l'eclittica e l'equatore.
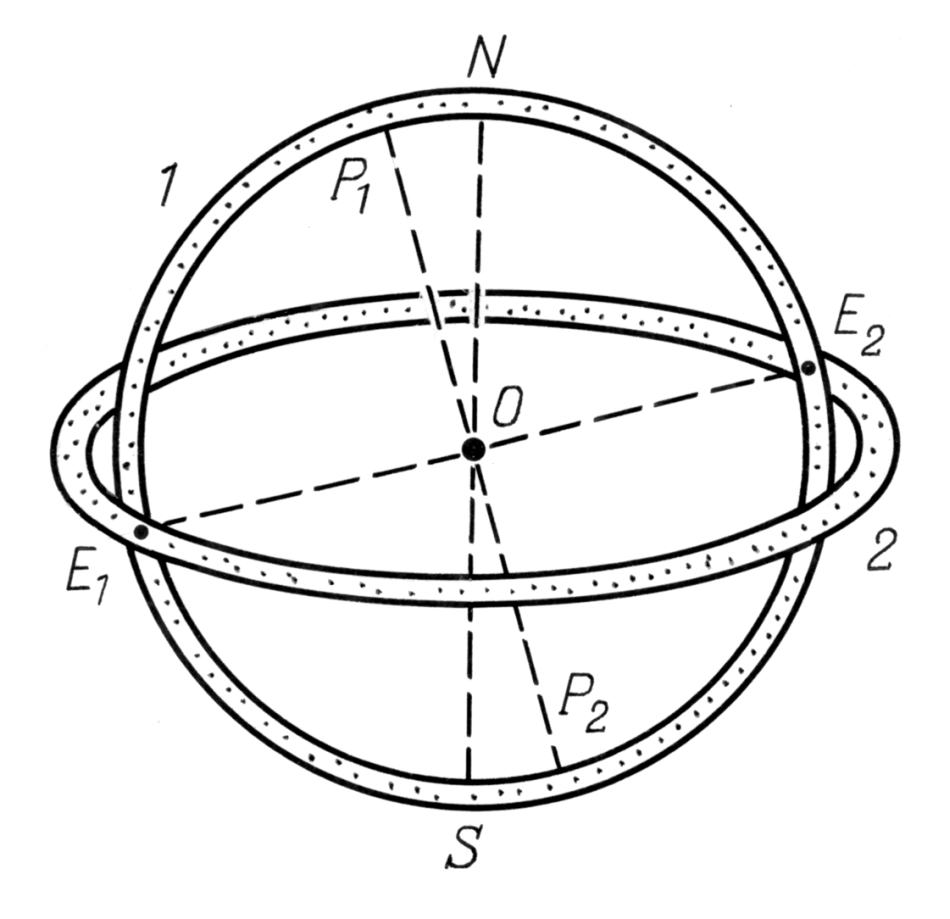
Figura 1.9.
Lo schema dell’astrolabon (armilla).

Figura 1.10.
Lo schema della sfera armillare.
Il secondo strumento descritto da Tolomeo è l'astrolabon, che ai nostri giorni viene spesso chiamato “astrolabio”. Quest'ultimo termine è di origine medievale. Secondo la storia dell'astronomia di Scaligero, il significato del termine “astrolabon” è cambiato nel corso del tempo. Ci viene detto che “nell'antichità profonda”, ovvero intorno all'inizio della nuova era, il termine “astrolabon” era usato per riferirsi allo strumento che descriveremo tra poco. Tolomeo ne usò uno. Tuttavia, nel Medioevo lo strumento in questione era già conosciuto come sfera armillare, o “armilla”. Alcuni astronomi moderni sono dell'opinione che nell'Almagesto Tolomeo descriva la sfera armillare o l'astrolabon, non il vero astrolabio (vedi [395], per esempio). Secondo il famoso astronomo Robert Newton, “è probabile che intorno alla fine del Medioevo il termine “astrolabio” si riferisse al dispositivo utilizzato per misurare l'altezza di un corpo celeste sopra l'orizzonte. Per quanto riguarda il dispositivo che andremo a descrivere [in conformità con le indicazioni di Tolomeo - autore], a quel tempo era meglio conosciuto come sfera armillare, che è il lontano antenato delle moderne strutture portanti dei telescopi” ([614], pagina 151).
Al fine di evitare confusione con i termini, descriveremo i due strumenti separatamente: l'astrolabon di Tolomeo e l'astrolabio, ossia lo strumento medievale il cui nome è praticamente identico a quello dell'astrolabon di Tolomeo. Gli elementi principali dell'astrolabon (armilla) sono mostrati nella Figura 1.9. Nella Figura 1.10 possiamo vedere lo schema principale della sfera armillare. La Figura 1.11 e 1.11a ci mostrano “la sfera armillare medievale, che secondo gli storici è del tipo di quella di Tolomeo. Il suo diametro è pari a 1,17 metri. Questo strumento fu prodotto quando l'epoca di Tolomeo venne già considerata antica; apparteneva a Tycho Brahe, il famoso astronomo del XVI secolo” ([1029],pagina 13). L'implicazione è che gli strumenti astronomici rimasero gli stessi per millecinquecento anni. Come possiamo vedere, gli strumenti del “antico” Tolomeo del II secolo d.C. e quelli dello scienziato del XVI secolo Tycho Brahe, erano quasi identici, come se fossero stati realizzati nella stessa bottega medievale. Un antico disegno della grande sfera armillare di Tycho Brahe può essere visto nella Figura 1.12.
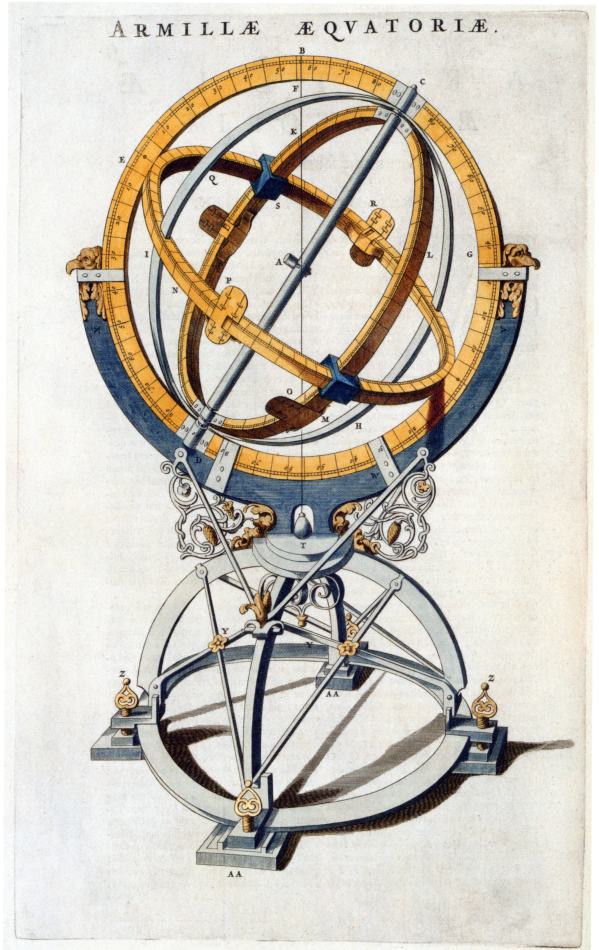
Figura 1.11.
La sfera armillare realizzata nel XVI secolo;
apparteneva a Tycho Brahe (1598).
È quasi indistinguibile dallo strumento utilizzato
dal "antico" Tolomeo nel II secolo d.C.
Con tutta probabilità questi strumenti
risalgono alla stessa epoca,
il XV-XVII secolo.
Tratta da [1029], pagina 13.

Figura 1.12.
“La grande sfera armillare di Tycho Brahe
per misurare le distanze angolari tra i luminari”
(da Mechanics Rejuvenated by Astronomy,
un'opera di Tycho Brahe. Windsbeck, 1598.
Tratta da [926], pagina 62.
Ora dobbiamo descrivere ai lettori l'uso corretto di questo strumento, come pure menzionare i principi astronomici della sua costruzione. L'elemento principale della sfera armillare comprende due anelli metallici, perpendicolari tra loro e rigidamente uniti nei punti E1 ed E2. D'ora in poi indicheremo gli anelli come il “primo” e il “secondo” (vedi la Figura 1.9). Il primo anello ruota attorno all'asse NS, che è parallela all'asse della rotazione tellurica. Il centro di entrambi gli anelli è il punto O; P1P2 è la perpendicolare al piano del secondo anello.
Ora descriveremo come si usa l'armilla per misurare l'angolo tra l'eclittica e l'equatore. Il momento più appropriato per queste misurazioni cade durante il giorno del solstizio di estate o di inverno. Il punto corrispondente sull'orbita terrestre è segnato nella Figura 1.13 con O'. Non importa se corrisponde al solstizio d'estate o d'inverno. Prendiamo in considerazione il piano che attraversa il vettore radiale CO', dove C è il Sole e l'asse terrestre viene indicato con NO'. Poiché O' è il punto del solstizio, questo piano sarà ortogonale al piano dell'eclittica, in quanto attraversa la superficie terrestre lungo il meridiano, vedi la Figura 1.13.
Supponiamo che l'armilla sia stata installata da qualche parte lungo questo meridiano. Lo strumento può essere posizionato in qualsiasi punto della superficie della Terra, ma le misurazioni devono iniziare a mezzogiorno, ovvero quando lo strumento si trova sul meridiano che interseca detto piano con la superficie terrestre. Supponiamo che l'osservatore conosca la direzione dell'asse terrestre per questa parte della Terra; perciò l'asse NO dell'armilla deve essere orientato in questa direzione e parallelo all'asse NO', vedi la Figura 1.13. Quindi, ruotando il primo anello metallico attorno all'asse NS dell'armilla, lo installeremo sul piano del meridiano e accadrà quando l'ombra del bordo esterno dell'anello coprirà esattamente la parte interna dell'anello. Infine, dopo aver fissato il piano del primo anello, dobbiamo fare in modo che il secondo sia ortogonale al primo, in modo che la sua parte interna sia coperta dall'ombra proiettata dalla sua parte esterna. La Figura 1.13 dimostra che, a seguito di queste manipolazioni, il secondo anello finisce esattamente nel piano dell'eclittica (più precisamente sarà parallelo al piano dell'eclittica). Dal momento che abbiamo fissato entrambi gli anelli nella necessaria posizione, la dovremo fissare la perpendicolare P1P2 al secondo anello, segnando così la coppia dei punti polari P1 e P2 sul primo anello. Pertanto, saremo in grado di misurare l'angolo P1ON con sufficiente precisione; ovviamente sarà uguale all'angolo tra l'eclittica e l'equatore.
Abbiamo descritto il metodo che presumibilmente usavano gli antichi astronomi. Nonostante la semplicità geometrica dell'idea, si possono vedere chiaramente le numerose complicazioni che introducono vari errori nel valore numerico dell'angolo misurato. In particolare, l'osservatore dovrà conoscere i seguenti parametri:
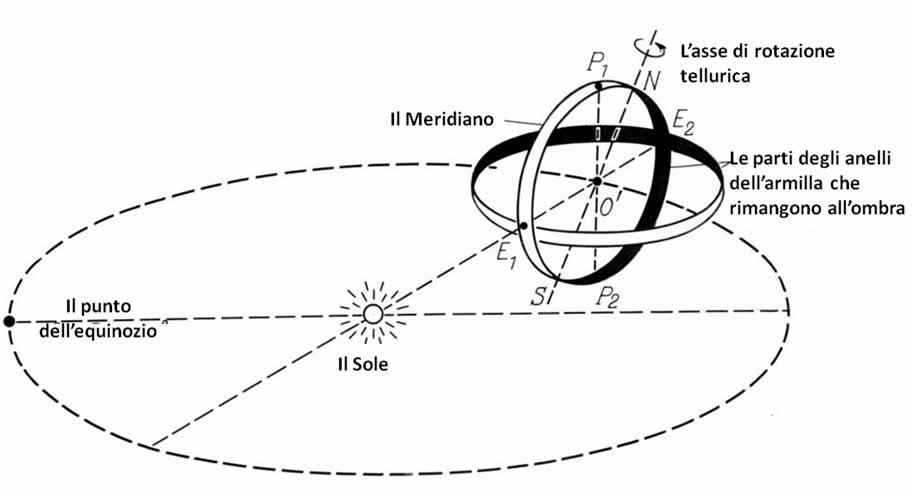
Figura 1.13.
Lo schema di utilizzo dell'armilla per la misurazione dell'angolo tra l'equatore e l'eclittica.
- la direzione dell'asse ON, che è parallela all'asse della Terra;
- il giorno del solstizio;
- il mezzogiorno in questo punto della superficie terrestre.
R. Newton fece la seguente osservazione giustificata: “Il principale difetto di questo strumento è che bisogna essere abbastanza veloci quando lo si utilizza, poiché la rotazione della Terra ha un effetto negativo sulla precisione del dispositivo” ([614], pagina 150). In effetti, nella Figura 1.13 possiamo vedere che la rotazione terrestre inizia a far girare lo strumento attorno all'asse O'N, invalidando le considerazioni di cui sopra.
Per essere precisi, i punti O (il centro dell'armilla) e O' (il centro della Terra), come da Figura. 1.13, sono differenti. La distanza tra i due è pari al raggio della Terra. Tuttavia, questa discrepanza è trascurabilmente piccola per i calcoli di cui sopra. Pertanto, possiamo supporre che O = O' per quanto riguarda le misurazione mostrate nella Figura 1.13.
Torniamo alla misurazione delle coordinate dell'eclittica con l'aiuto dell'armilla.
Dopo aver installato correttamente il dispositivo come descritto sopra, lo si deve sintonizzare per un breve periodo sul sistema delle coordinate dell'eclittica, vale a dire che il piano del secondo anello E1E2 deve essere parallelo al piano dell'eclittica. I punti E1 ed E2 devono corrispondere ai punti del solstizio. Si presume che entrambi gli anelli siano graduati. Pertanto, possiamo definire inequivocabilmente i punti R1 e R2 sul secondo anello, che dovranno corrispondere agli equinozi. Devono dividere gli archi E1 ed E2 in due metà. I punti R1 e R2 sono stati omessi dalla Figura 1.13 per non riempire troppo l'illustrazione. Quindi, quello che c'è sul secondo anello è una scala con un punto di riferimento iniziale fisso (per esempio R1, che è il punto dell'equinozio di primavera). Possiamo così misurare le lunghezze e le latitudini eclittiche dei punti sulla sfera celeste che rappresentano le stelle.
Tuttavia, ribadiamo che la rotazione giornaliera della Terra fa scattare rapidamente la precisione dello strumento. Pertanto, è necessario avere un cronometro preciso per poter compensare la rotazione della Terra e sintonizzare lo strumento. Ecco come sono costruiti i moderni strumenti di misurazione: la rotazione della Terra viene compensata da un sistema di tracciamento automatico.
Per facilitare le misurazioni delle coordinate eclittiche degli oggetti celesti, di solito viene aggiunto un terzo anello alla sfera armillare, uno in grado di ruotare. A sua volta, l'asse della rotazione può scorrere lungo il secondo anello che è posizionato sul piano dell'eclittica. Omettiamo i dettagli poiché sono di scarsa importanza per noi.
Consideriamo ora il terzo strumento, ossia il quadrante (vedi le Figure 1.14, 1.14a e 1.14b). Questo strumento si basa sul circolo meridiano ed ha un puntatore al centro che è perpendicolare al piano del circolo.
L'ombra del puntatore cade sulla parte inferiore (settentrionale) del circolo meridiano e può spostarsi all'interno di un quarto della circonferenza. Pertanto, al fine di misurare l'altezza del sole è sufficiente graduare un quarto dell'anello. Il quadrante è quindi un sorta di piastra con il quarto graduato del circolo installato sul piano del meridiano. L'altezza del sole sopra l'orizzonte a mezzogiorno viene indicata dall'ombra del puntatore che cade sulla scala graduata.

Figura 1.14.
Lo schema del quadrante.

Figura 1.14a.
Quadrante medievale. Preso da [1036: 1], pag. 96.
Nella Figura 1.15 possiamo vedere un quadrante astronomico preso da un libro medievale del 1542 di Oronzio Fineo ([1029],pagina 19).
La Figura 1.16 ci mostra il piccolo quadrante con un raggio di 39 centimetri, che apparteneva a Tycho Brahe ([1029], pagina 26).
La Figura 1.16a ci mostra l'instrumentum parallaticum di Tycho Brahe, ([1036: 1], pagina 90).
Nella Figura 1.17 possiamo vedere il sestante di Tycho Brahe con un raggio di 1,55 metri, mentre nella Figura 1.18 c'è un altro sestante di Tycho Brahe della stessa dimensione ([1029], pagina 26).
Nella Figura 1.19 vediamo l'astronomo Hevelius ritratto mentre esegue delle misurazioni con l'aiuto di un sestante ([1029], pagina 67).

Figura 1.15.
. Il quadrante astronomico tratto
da un libro medievale di Fineo.
Preso da [1029], pagina 19.

Figura 1.19.
L'astronomo Hevelius mentre, assistito dalla moglie,
sta usando un grande sestante per eseguire
delle osservazioni.
Antica incisione risalente al 1673.
Presa da [1029], pagina 67.
Il quarto strumento è l'astrolabio (vedi la Figura 1.20). L'astrolabio medievale è una piastra tonda metallica avente un diametro di circa 50 centimetri, con un anello graduato montato rigidamente su uno dei suoi bordi. Al centro dell'anello si trova è una plancia mobile con visori montata sull'asse perpendicolare al centro del cerchio. Lo strumento può essere sospeso verticalmente; c'è un anello speciale sul bordo della piastra, che serve proprio a questo scopo. Il piano del cerchio sospeso in verticale può essere diretto verso un corpo celeste, come pure la plancia mobile rotante. E' così che veniva misurata l'altezza del corpo sopra l'orizzonte. A parte questo, dopo aver misurato l'altezza del Sole a mezzogiorno, si poteva anche misurare la latitudine di osservazione. La precisione di questa misurazione era piuttosto bassa a causa della natura primitiva del metodo utilizzato. Si ritiene che lo strumento in questione potesse misurare la latitudine del punto di osservazione con la precisione di diversi gradi d'arco ([614]).
Nella Figura 1.21 possiamo vedere un vecchio astrolabio del 1532 (Georg Hartmann, Norimberga). Si vede la parte anteriore e quella posteriore dell'astrolabio.
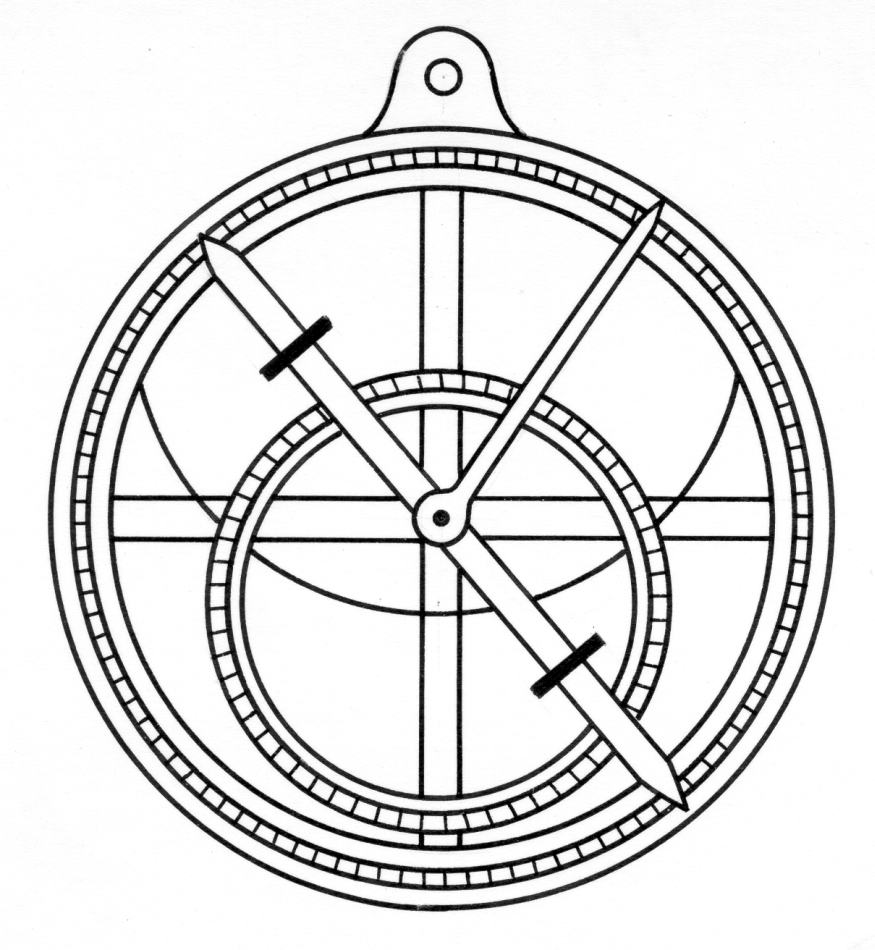
Figura 1.20.
Lo schema dell’astrolabio.

Figura 1.21.
L'astrolabio di Georg Hartmann di Norimberga
. Possiamo vedere sia il lato di fronte che il retro dello strumento.
Tratto da [1029], pagina 15.

Figura 1.21a.
Astrolabio persiano del XVIII secolo.
Museo Whipple di Storia della Scienza.
Tratto da Internet, Wikipedia.

Figura 1.21b.
L'astrolabio universale.
L'Aia, il maestro F. Fibich.
La metà del XVII secolo.
La foto è stata scattata
da A. T. Fomenko
nel 2013 alla mostra
“La Russia e Olanda”,
Museo Statale di Storia.

Figura 1.21c.
. L'astrolabio sferico. Oxford,
Museo di Storia della Scienza.
Tratto da Internet, Wikipedia.

Figura 1.22.
Lo strumento medievale noto come turketum (lo strumento turco).
Venne progettato per stimare i diversi tipi di coordinate degli oggetti celesti.
Fu anche utilizzato nella teoria planetaria tolemaica (Werner, 1533).
Tratto da [1029], pagina 18.
Nella Figura 1.22 presentiamo una vecchia immagine del famoso strumento astronomico medievale noto come “lo strumento turco”, o “torquetum”. Gli esperti in storia della scienza ci dicono quanto segue: “Il “torquetum” (o turketum), il cui nome può essere tradotto con “lo strumento turco”, era caratteristico dell'astronomia europea medievale e incarnava sia l'eredità intellettuale di Tolomeo che la tradizione islamica ... Il torquetum veniva usato per misurare tutti e tre i tipi di coordinate astronomiche e le conversioni tra diversi tipi di coordinate che furono stipulate dalla teoria planetari di Tolomeo” ([1029], pagina 17). Lo strumento mostrato nella Figura 1.22 apparteneva a Pietro Apiano (1497-1552). Ci viene quindi detto che i turchi medievali “riportarono in vita” la teoria tolemaica delle misurazioni e la fabbricazione degli strumenti necessari dopo molti anni di oblio, vale a dire millecinquecento anni dopo “l'antico” Tolomeo.
Stiamo iniziando a renderci conto che il turketum ottomano medievale era contemporaneo degli strumenti tolemaici. Questi strumenti furono realizzati nel XV-XVII secolo.
7. La misurazione del tempo e i relativi strumenti usati nelle osservazioni astronomiche medievali
Come abbiamo sottolineato in precedenza, al fine di condurre delle precise osservazioni astronomiche, gli astronomi antichi avevano bisogno di un cronometro con una lancetta dei minuti o qualcosa del genere. A tal riguardo sarebbe opportuno ricordare la storia della misurazione del tempo durante il Medioevo, in modo da poter confrontare la precisione dei dispositivi medievali con la precisione relativa delle coordinate incluse nei cataloghi stellari medievali, in particolare con il catalogo dell'Almagesto.
In linea di massima, va detto che il concetto di tempo era piuttosto idiosincratico nel medioevo. L’analisi dei documenti antichi dimostra che questo concetto differiva molto da quello moderno. In particolare, prima dell’invenzione dell’orologio il tempo veniva spesso considerato “antropomorfo”, più specificamente il suo carattere e la sua velocità dipendevano dalla natura degli eventi. Come già riportato in Cronologia 1, “prima del XIII-XIV secolo i dispositivi per la misurazione del tempo erano una rarità e un lusso. A volte non li avevano neppure gli scienziati. L’inglese Valcherius ... si rammaricava del fatto che la precisione delle sue osservazioni sull’eclissi lunare del 1091 fu compromessa dall’assenza di un cronometro” ([1461], pagina 68). Gli strumenti di bassa precisione per la misurazione del tempo furono introdotti nel Medioevo: “i tipici dispositivi per la misurazione del tempo in Europa medievale erano le meridiane ... le clessidre di sabbia e quelle ad acqua. Tuttavia, le meridiane erano utili solo durante le giornate di sole e le clessidre ad acqua rimasero una rarità” ([217], pagina 94).
Nella Figura 1.23 possiamo vedere gli anelli astronomici del XVII-XVIII secolo che venivano usati per raccontare il tempo in particolare attraverso il sole. Il metodo del loro utilizzo è mostrato in un vecchio disegno che riproduciamo nella Figura 1.24. Nella Figura 1.25 possiamo vedere delle vecchie clessidre.

Figura 1.23.
Lo strumento del XVII-XVIII secolo
che tra le altre cose fu utilizzato
per misurare il tempo solare.
Preso da [1029], pagina 21.

Figura 1.24.
Gli anelli astronomici di Gemma Frisius.
“Uno strumento equatoriale portatile che poteva essere utilizzato a qualsiasi latitudine...
per il cronometraggio del sole,
come pure per molte altre osservazioni astronomiche approssimative
(Apiano, 1539). Preso da [1029], pagina 21.

Figura 1.25.
Diversi tipi di clessidre antiche. Museo del Louvre, Parigi.
Tratta da Internet, Wikipedia.
La clessidra è stata anche esposta al Whipple Museum,
il museo di storia della scienza di Cambridge, [1029], p.31.
La produzione in serie delle clessidre ad acqua avvenne nel XIII-XIV secolo. Furono usate da Tycho Brahe (1546-1601). Le usava per misurare la velocità dei pianeti ([954], pagina 36). Nel Medioevo “la clessidra ad acqua era un dispositivo molto popolare, nonostante la sua bassa precisione. Per renderle più precise, i costruttori dovevano tener conto del fatto che l'acqua non lasciava il recipiente a velocità costante, ma dipendeva dalla pressione, vale a dire che maggiore è il livello dell'acqua nel recipiente, maggiore è la pressione. I costruttori delle clessidre ad acqua migliorarono un po' la costruzione rendendola più complessa, in modo che l'orologio non rallentasse mentre la cima del recipiente si svuotava ...Tuttavia, le clessidre ad acqua avevano una tolleranza di circa 10-20 minuti al giorno; nemmeno i migliori scienziati dell'epoca riuscirono a pensare a un modo per renderle sostanzialmente più precise” ([288], pagine 32-33).
Alla fine del IX secolo, per misurare il tempo furono ampiamente usate le candele. Per esempio, il re Alfredo d'Inghilterra durante i suoi viaggi prendeva delle candele di diversa lunghezza e ordinava di accenderle una dopo l'altra ([217], pagina 94). Questo metodo di cronometraggio era ancora usato nel XIII-XIV secolo durante il regno di Carlo V e di altri monarchi dell'epoca. Le candele usate per misurare il tempo erano conosciute come “orologio di fuoco”.
Molti paesi conservarono questo metodo di misurazione per molto tempo. “I giapponesi, ad esempio, fino a 200 anni fa usavano dei dispositivi di cronometraggio costituiti da vari bastoncini di incenso appoggiati l'uno contro l'altro. Si poteva, per così dire, “annusare” l'ora dal loro aroma. Anche gli “orologi di fuoco” usati dagli europei erano delle candele con dei segni speciali” ([954], pagina 37). Possiamo vedere che tutti questi “antichi” metodi di cronometraggio furono usati relativamente di recente; bisogna pensare che non vennero inventati molto tempo fa.
Gli “orologi di fuoco” furono usati per molto tempo anche in Cina. Con delle speciali polveri di legno creavano una pasta che poi la arrotolavano a forma di bastoncini, spirali e via dicendo. Occasionalmente, in determinati punti di quei bastoncini venivano legate delle sfere di metallo. Quando il bastone bruciava, la cenere cadeva in un vaso ed emetteva un suono. “La precisione degli “orologi di fuoco” lasciava molto a desiderare; a parte la difficoltà di creare bastoncini e candele perfettamente uniformi, la velocità della loro combustione dipendeva sempre dalle condizioni atmosferiche (vento, aria fredda, ecc.)” ([288],pagine 30-31).
La clessidra a sabbia era un altro dispositivo di cronometraggio molto popolare nel Medioevo. “La precisione della clessidra dipende dalla stabilità del flusso di sabbia. Per rendere la clessidra più precisa, è necessario usare una sabbia morbida, secca e più uniforme possibile, in modo che non formi grumi all'interno del recipiente. Gli artigiani medievali del XIII secolo riuscirono in questa impresa dopo aver fatto bollire una miscela di sabbia e polvere di marmo con vino e succo di limone; poi la scremavano, la facevano asciugare e quindi ripetevano il processo nove volte. Nonostante tutti questi accorgimenti, la clessidra è rimasta uno strumento di cronometraggio di bassa precisione” ([288], pagina 30). Nel XII secolo, i sovrani secolari di Mons che volevano iniziare un processo in un determinato momento, dovevano consultarsi con le autorità ecclesiastiche circa il momento della giornata” ([1037], pagine 117-118).
Oggi si ritiene che la prima menzione riguardo a un cronometro meccanico risalga alla fine del VI secolo d.C. ([797]). Quindi i dispositivi scomparvero per molto tempo per poi riaffiorare già durante il Rinascimento. Secondo gli esperti in storia della scienza, “il primo orologio meccanico venne realizzato da artigiani italiani ingegnosi e curiosi nel XIII secolo” ([954], pagina 38). Il principio della loro costruzione è abbastanza semplice: una corda con un peso alla sua estremità viene avvolta a un albero orizzontale. Il peso fa svolgere la corda, la quale fa ruotare l'albero. Se dovessimo attaccare una lancetta all'albero, quella ci direbbe l'ora. Nonostante la semplicità del principio, la difficoltà nella sua realizzazione pratica consistette nello stabilizzare la frequenza di rotazione dell'albero. Questo scopo venne raggiunto mediante l'utilizzo di numerose ruote che trasferivano la rotazione dell'albero alla lancetta e di regolatori ingegnosi di ogni tipo, installati per aumentare o diminuire uniformemente la velocità di rotazione dell'albero. “Gli orologi meccanici erano delle costruzioni di dimensioni formidabili. Gli enormi meccanismi degli orologi venivano installati sulle torri delle cattedrali e dei palazzi” ([954], pagina 38). “Il volano di un orologio di Tycho Brahe aveva 1200 tacche e un diametro di 91 centimetri” ([288], pagina 35). “Le ruote di alcuni orologi pesavano centinaia di chili. A causa del grande peso e del sostanziale attrito delle loro parti, gli orologi meccanici a ruote richiedevano una costante lubrificazione e manutenzione. Il tasso di tolleranza giornaliero di quegli orologi era pari a diversi minuti” ([288], pagina 35).
“Fu solo nel XV secolo che la molla sostituì l'albero e la corda nei meccanismi degli orologi. Il peso degli orologi si ridusse drasticamente. Gli artigiani dei primi del XVI secolo erano dei maestri nel costruire orologi mobili a molla che pesavano 3 o 4 chili. Erano gli antenati piuttosto pesanti del moderno orologio meccanico” ([954], pagina 39).
L'invenzione dell'orologio con la dei minuti deve essere stata seguita dalla compilazione di un catalogo stellare longitudinale più o meno preciso. Qual è il significato della lancetta dei minuti? La questione è che la sfera celeste e tutti gli oggetti che si vedono sopra ruotano alla velocità di un grado ogni 4 minuti; pertanto, una stella percorre 15 gradi d'arco al minuto. I cataloghi stellari contengono le coordinate delle stelle indicate per gradi d'arco; quindi per ottenere una tolleranza di precisione del catalogo pari a circa 15 gradi d'arco, bisogna essere in grado di tracciare l'intervallo di un minuto su un dispositivo per la misurazione del tempo. Una tolleranza di circa 10 minuti (come ad esempio nell'Almagesto) ha bisogno della capacità di misurare intervalli di tempo affidabili di 40 secondi. Maggiore è la precisione di un catalogo, maggiore deve essere la precisione dei dispositivi di cronometraggio. Ovviamente, gli osservatori potrebbero usare la loro intuizione per misurare dei brevi intervalli di tempo (un minuto e anche meno), ma ciò significherebbe avere degli errori soggettivi nel catalogo.
Per cui, gli astronomi antichi che affermavano che i loro cataloghi avevano una tolleranza di 10', dovevano per forza avere a loro disposizione un cronometro con la lancetta dei minuti o qualche cosa di simile. Tuttavia, Tolomeo, il quale fornisce la descrizione dettagliata di tutti gli strumenti necessari per misurare le coordinate stellari (la sfera armillare, ecc...) non menziona mai alcun cronometro e si astiene del tutto dal discutere il problema del cronometraggio e la sua relazione diretta con le osservazioni della sfera celeste, che è in costante movimento.
Come vedremo tra poco, l'ipotesi che i cronometri dotati di lancetta dei minuti possano essere esistiti nel II secolo d.C., contraddice le informazioni di Scaligero sulla storia dei dispositivi di cronometraggio.
Inoltre, quanto sopra implica che se dovessimo scoprire davvero una sorta di catalogo la cui tolleranza di precisione equivale a 10 gradi d'arco, come ha dichiarato l'autore dell'Almagesto, e questa tolleranza fosse verificata da uno studio statistico, avremmo un'ottima ragione per supporre che il compilatore del catalogo abbia utilizzato un orologio con la lancetta dei minuti o un suo equivalente.
Secondo la storia della misurazione del tempo, la lancetta delle ore fu introdotta nel meccanismo di una clessidra ad acqua nel XIII secolo d.C. ([544], Volume 4, pagina 267) o persino più tardi. I dispositivi di cronometraggio in questione non avevano il pendolo, per cui erano di bassa precisione. Fu solo nel XIV secolo d.C. che in alcune città dell'Europa medievale apparvero le prime torri con orologio meccanico (Milano nel 1306 e Padova nel 1344). Fu riferito che vennero costruite da un certo Dondi Horologiu. Gli orologi dotati di molle mosse da un peso furono introdotti solo nel XV secolo. Walther fu il primo ad usarli per le osservazioni astronomiche; venne seguito da molti altri compreso Tycho Brahe ([544], Volume 4, pagine 267-268).

Figura 1.26.
Il primo cronometro creato da John Harrison nel 1735.
L'altezza dello strumento è di 408 millimetri.
Presa da [1029], pagina 140.
Secondo la storia della scienza, “inizialmente, molti orologi meccanici avevano solo la lancetta delle ore. Nella metà del XVI secolo fu introdotta la lancetta dei minuti, mentre l'invenzione della lancetta dei secondi ebbe luogo 200 anni dopo” ([954], pagina 39). L'invenzione della lancetta dei minuti dell'orologio meccanico viene solitamente datata al 1550 d.C. ([288], pagina 36). Si ritiene che il primo cronometro fu costruito nel XVIII (1785, da parte di John Harrison). Harrison visse intorno al 1683-1776 ([1029], pagina 139). Il cronometro di Harrison è uno strumento abbastanza complesso; lo potete vedere nella Figura 1.26.
Il moderno orologio meccanico, incluso il pendolo, fu inventato da Huygens nel 1657 ([797]). Nel 1561 fu costruito l'osservatorio di Kassel; si trattò di una costruzione unica, poiché fu la prima ad incarnare il principio del tetto rotante (dispositivo utilizzato nella maggior parte degli osservatori moderni). Dopo la morte di Regiomontano e Walther, Guglielmo IV langravio d'Assia-Kassel (1532-1592), il creatore di detto osservatorio, condusse moltissime osservazioni delle stelle immobili (vedi il Capitolo 11 più avanti). In generale, “lo scopo principale dell'osservatorio di Kassel fu la compilazione di un catalogo stellare ... L'innovazione più notevole fu l'orologio utilizzato per il cronometraggio e le misurazioni che coinvolsero il moto della sfera celeste. La costruzione di un orologio la cui precisione era adatta a tal fine, deve la sua corretta implementazione al genio meccanico di Bürgi [1522-1632 - autore], in particolare alla sua scoperta che l'orologio poteva essere regolato dal pendolo; a quanto pare non tentò nemmeno di far diventare pubblica questa invenzione, per cui il pendolo venne reinventato prima che tutti potessero riconoscerlo [in riferimento alla scoperta di Galileo e Huygens - autore]. Nel 1586 furono annotate con la massima cura le posizioni di 121 stelle, ma il catalogo completo, che doveva contenere più di 1000 stelle, non venne mai finito” ([65], pagina 118).
L'attività di Tycho Brahe, che operò nella stessa epoca, ben presto superò completamente tutte le imprese dell'osservatorio di Kassel. È abbastanza curioso che gli scienziati dell'osservatorio di Kassel avessero già usato la compensazione della rifrazione per contrastare gli errori introdotti nell'atmosfera dalla rifrazione della luce solare ([65], pagina 118).
Fu solo al tempo di Huygens che l'orologio divenne parte integrante di molti strumenti astronomici: “Una delle invenzioni di Huygens rivoluzionò completamente l'arte delle osservazioni astronomiche precise. Huygens attaccò un pendolo all'orologio messo in moto dai pesi, in modo tale che l'orologio mantenesse il pendolo in movimento, che a sua volta regolava il movimento dell'orologio.
È probabile che, verso la fine della sua vita, Galileo abbia pensato di unire il pendolo e il meccanismo dell'orologio, ma non abbiamo le prove che sia mai riuscito a dare vita a questa idea.
Questa invenzione ci ha dato l'opportunità di fare delle osservazioni precise; notando il divario tra due stelle che attraversano il meridiano, conoscendo la velocità del moto della sfera celeste si può dedurre che il loro angolo di distanza verso ovest o est.
Picard fu il primo ad apprezzare l'importanza di questa invenzione per l'astronomia, introducendo un corretto strumento di cronometraggio nell'Osservatorio di Parigi di recente costruzione” ([65], pagina 177).