CAPITOLO 5
L’analisi degli errori sistematici dei cataloghi stellari
4. La variazione dei parametri γstat(t) e φstat(t) nel corso del tempo.
Prima abbiamo ipotizzato che il momento t è fisso. Consideriamo ora in che modo lo scorrere del tempo influenzi il comportamento dei valori calcolati γstat e φstat.
Questo comportamento può essere determinato dalle formule riportate nel paragrafo precedente. Queste formule contengono i valori Li(t) e Bi(t) che definiscono la dipendenza temporale di γstat e φstat. I cambiamenti delle longitudini (Li(t)) e delle latitudini (Bi(t)) nel corso del tempo sono stati studiati abbastanza bene, vedere il Capitolo 1. I rispettivi calcoli erano di natura abbastanza complessa e hanno richiesto l'uso del computer per un calcolo quantitativo della stima della dipendenza temporale di γstat(t) e φstat(t), vedere il Capitolo 6 dove analizzeremo semplicemente il comportamento qualitativo all'interno di queste funzioni.
Prendiamo in considerazione ancora una volta la sfera celeste, ipotizzando per semplicità che tutte le stelle là sopra siano immobili, tornando così alle concezioni di Tolomeo, anche se solo per semplificare l'argomentazione e i calcoli. Possiamo benissimo farlo poiché la percentuale delle stelle con velocità notevole di moto proprio (quelle che si muovono di diversi gradi d'arco nel corso dell'intervallo temporale di 2500 anni preso in esame) è relativamente basso. Quelle stelle influiscono difficilmente sul calcolo dei parametri γstat(t) e φstat(t) di cui ci stiamo occupando ora.
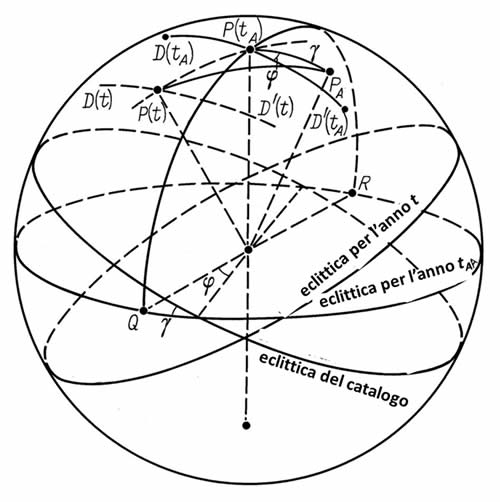
Nella Figura 5.4 si può vedere sia la sfera celeste che l'eclittica effettiva per la compilazione del catalogo nell'epoca tA. Sarebbe opportuno confrontare le Figure 5.1 e 5.4. Nell'epoca tA che a noi resta sconosciuta, il polo dell'eclittica P(tA) occupava una certa posizione sulla sfera celeste. Ovviamente, il compilatore del catalogo non fu idealmente preciso nell'indicazione dell'eclittica sulla sfera celeste. Pertanto il polo PA della sua “eclittica del catalogo” assunse una posizione diversa da quella di P(tA).
Disegniamo l'arco di un grande cerchio che collegherà il polo P(tA) con i rispettivi punti Q e R dell'equinozio primaverile e autunnale. Inoltre, disegneremo l'arco del grande cerchio D(tA)D'(tA) che passerà attraverso P(tA) e attraverserà l'arco di recente costruzione QP(tA)R nell'angolo retto del punto P(tA). Se conoscessimo la data tA, il metodo dei minimi quadrati descritto nel paragrafo 3 ci darebbe l'opportunità di trovare i parametri γ e φ che definiscono la disposizione in comune dell'eclittica per l'epoca tA e l'eclittica del catalogo. La Figura 5.4 dimostra che proprio questi angoli definiscono anche la disposizione reciproca dei poli P(tA) e PA sulla sfera celeste, vale a dire che il valore di γ è uguale alla lunghezza dell'arco P(tA)PA nei valori dell'arco, mentre l'angolo φ è pari all'angolo PAP(tA)D'(tA). Come abbiamo sottolineato nel Capitolo 1, la posizione celeste dell'eclittica si altera nel corso del tempo. Si tratta della manifestazione dell'effetto di fluttuazione dell'eclittica. Perciò, il polo dell'eclittica per il momento t che differisce da tA, dovrà essere situato nel punto P(t) che differirà anch'esso da P(tA).
Nella Figura 5.4 la traiettoria del polo dell'eclittica sulla sfera celeste è indicata con una linea tratteggiata, quella che attraversa i punti P(t) e P(tA). Pertanto, per poter abbinare l'eclittica dell'epoca t al catalogo dell'eclittica, si devono sovrapporre l'uno sull'altro i poli PA e P(t). La lunghezza dell'arco P(t)PA è pari al valore di γstat(t), mentre la posizione dell'asse di rotazione dell'eclittica che fornisce la sovrapposizione può essere parametrizzata dall'angolo PAP(t)D'(t) dove l'arco D(t)D'(t) è “parallelo” all'arco D(tA)D'(tA).
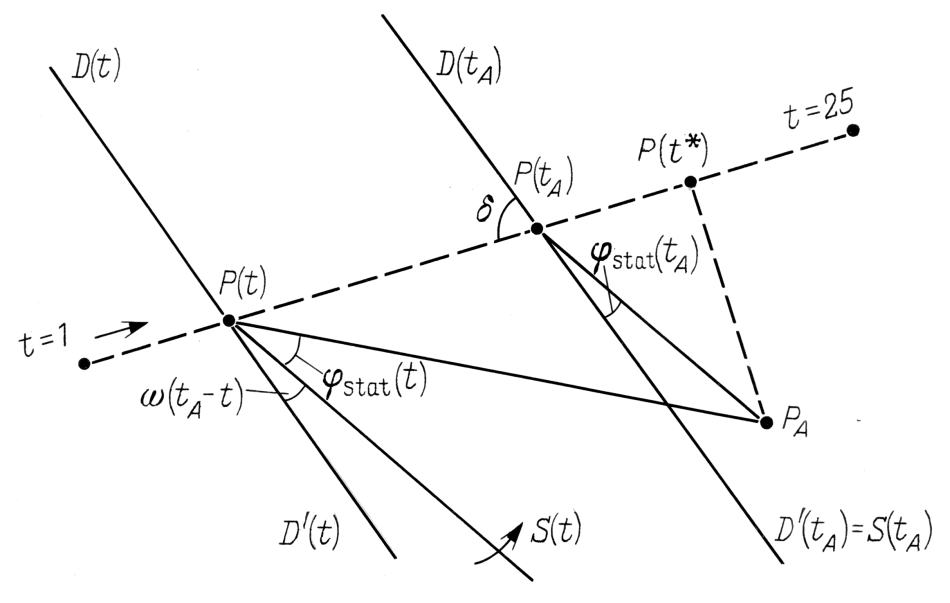
Per poter meglio comprendere il comportamento quantitativo delle funzioni γstat(t) e φstat(t), usiamo un disegno bidimensionale che raffigura solo gli spostamenti dei poli dell'eclittica. E' consentito poiché si sa a priori che i valori dei loro spostamenti rientrano nello spazio di un grado. Dobbiamo quindi fare una copia bidimensionale della parte polare della Figura 5.4: vedi la Figura 5.5.
Come appare evidente dalla Figura 5.5, il polo effettivo dell'eclittico si sposta nel corso del tempo a causa delle fluttuazioni dell'eclittica. Per l'intervallo in esame il valore di questo spostamento equivale a soli 25' di media, per cui possiamo disegnarlo come una linea retta (vedi la linea tratteggiata nella Figura 5.5). Il moto del polo dell'eclittica lungo questa linea può essere considerato uniforme con un grado abbastanza alto di precisione. Quindi, la distanza tra i poli P(t) e P(tA), ad esempio, dovrà essere uguale a υ(tA - t), dove v è la velocità di moto del polo dell'eclittica. Questa velocità si avvicina a 0,01' all'anno. Come abbiamo detto in precedenza, nell'epoca di osservazione tA il compilatore del catalogo ha commesso un errore nella stima del piano dell'eclittica, che ha provocato lo spostamento del polo dell'eclittica del catalogo nel punto PA, che differisce da P(tA). Ciò dovrebbe risultare nella perpendicolare tra PA e la traiettoria del moto del polo dell'eclittica la attraversa nel punto t* > tA. Come nel caso della Figura 5.5, questo errore del compilatore aggiungerà ovviamente un'età extra all'eclittica del catalogo, vale a dire che la farà corrispondere meglio all'eclittica dell'anno t*. Avviene il contrario se questa perpendicolare attraversa la traiettoria nel punto t* < tA; in questo caso l'errore dell'autore renderebbe il catalogo “più recente”. Per dare ai lettori un'impressione delle vero valore delle correlazioni, indicheremo che nell'Almagesto la distanza tra i poli dell'eclittica P(0) per il 1900 d.C. e P(19) per l'inizio dell'era dopo Cristo, equivale approssimativamente a 20', un valore che si avvicina a quello dell'errore γstat(tA).
In precedenza abbiamo menzionato che il valore γstat(tA) era pari alla lunghezza del segmento P(tA)PA, mentre φstat(tA) era uguale all'angolo PAP(tA)D'(tA). Analogamente, γstat(t) - P(t)PA. La linea orizzontale superiore si riferisce alla lunghezza del segmento. Tuttavia, l'angolo PAP(t)D'(t) non è uguale a φstat(t), in quanto nel momento t l'asse dell'equinozio di primavera si sposterà per il valore di ω(tA - t).
Qui ω rappresenta la velocità angolare annuale della precessione che approssimativamente è pari a 50", vedere il Capitolo 1. Questo spostamento corrisponde al valore dell'angolo D'(t)P(t)S(t) nella Figura 5.5. Pertanto, φstat(t) è uguale all'angolo PAP(t)S(t), dove l'angolo D'(t)P(t)S(t) = ω(tA - t).
Per evitare le indicazioni molto ingombranti, presumiamo che
| _______ | ________ | _______ |
| x(t) = P(t)P(tA), | y = P(tA)P(t*), | z = PAP(t*), |
| ψ(t) = ∠ PAP(t)D'(t), | δ = ∠ D(tA)P(tA)P(t). |
Il valore di γstat(tA) può essere descritto come l'errore di stima dell'eclittica; nell'Almagesto ha un ordine di 20'. L'angolo δ non dipende da t ed è pari all'angolo tra la direzione del moto del polo dell'eclittica e la linea D(tA)D'(tA) stimato sopra. È ovvio che
z = γstat(tA) sin(δ – φstat(tA)),
y = γstat(tA) cos(δ – φstat(tA)).
Poiché x(t) = v(tA- t), dalla Figura 5.5 abbiamo

Ovviamente, il valore minimo di questa funzione viene raggiunto con t = t*. Se stessimo studiando il caso di |t - tA| << |tA - t*|, la funzione di γstat(t) si comporterebbe quasi come se fosse lineare:
γstat(t) ≈ γstat(tA) + υcos(δ - φstat(tA)) (tA - t)
La funzione φstat(t) è anche comoda per trovare:
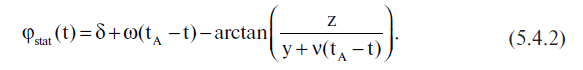
Di nuovo, se |t - tA| << |tA - t*|, si potrebbe usare l'approssimazione lineare:
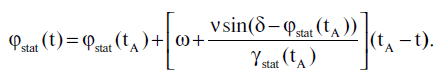
Naturalmente, le formule a cui arriviamo possono darci solo un'idea generale del carattere delle funzioni γstat(t) e φstat(t). Nella Figura 5.6 possiamo vedere una rappresentazione approssimativa di queste funzioni, ottenuta dalle formule 5.4.1 e 5.4.2. È ovvio che la loro forma effettiva dipende dal tasso di errore riguardo l'accuratezza del compilatore del catalogo, ovvero i valori di γstat(tA) e φstat(tA). Le formule 5.4.1 e 5.4.2 definiscono anche la natura della dipendenza βstat(t), vedere la formula 5.2.1.
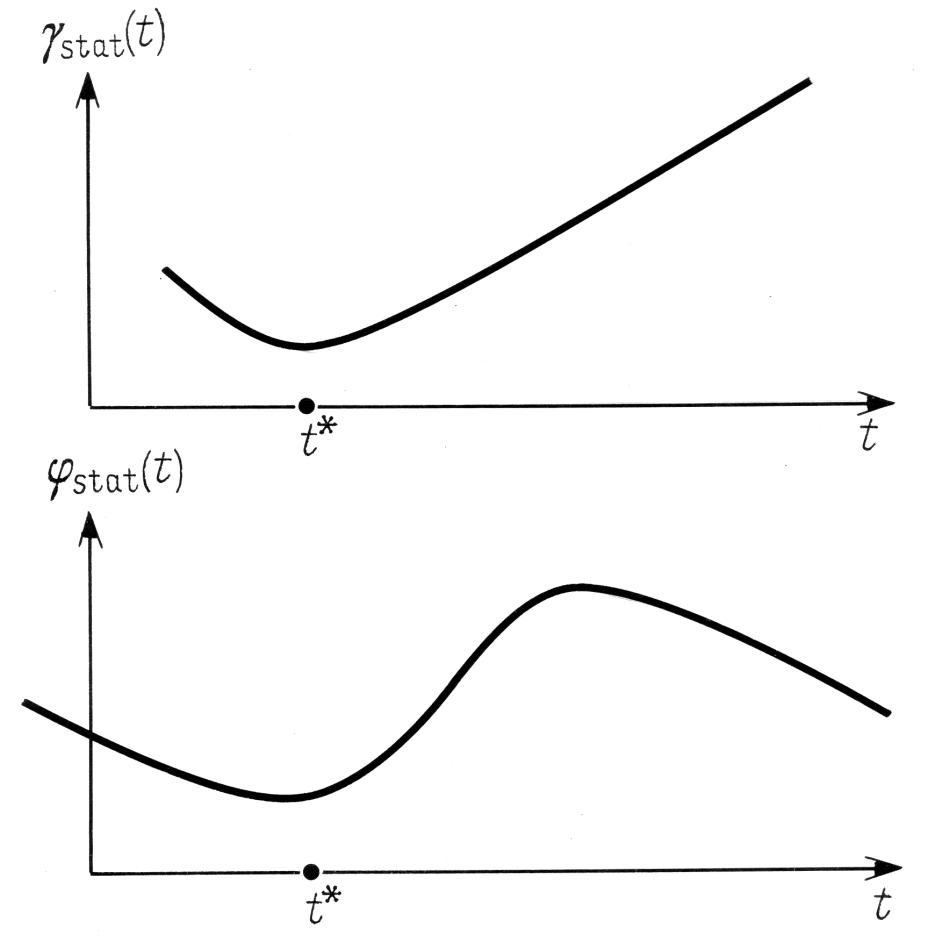
Figura 5.6.
Vista approssimativa delle funzioni γstat(t) e φstat(t).
Discutiamo il significato geometrico di questi calcoli. Prendiamo in considerazione le coordinate tolemaiche di alcuni gruppi stellari, presumendo che le osservazioni siano state eseguite nel momento temporale t. Quindi dobbiamo compensare l'errore sistematico γstat(t), φstat(t) o ruotare l'intero gruppo di un angolo γstat(t) attorno all'asse che si trova alla distanza φstat(t) dall'asse dell'equinozio. Supponiamo di essere stati perfettamente precisi nella stima dell'errore sistematico, per cui il polo PA dell'eclittica del catalogo si sovrappone al polo effettivo P(t). Ovviamente, tale sovrapposizione non renderà pari a zero le discrepanze latitudinali delle stelle, poiché il catalogo contiene anche degli errori casuali. Tuttavia, questi errori non influenzano la posizione del polo dell'eclittica in quanto hanno un valore medio nullo, o piuttosto lo influenzano in misura molto ridotta, che è inversamente proporzionale alla quantità del gruppo di stelle oggetto di studio.
Nella Figura 5.5 possiamo vedere che c'è un solo modo possibile per cui lo spostamento del polo PA verso il punto P(t) può essere scomposto in due spostamenti: da PA a P(tA) e da P(tA) a P(t). I parametri γstat(tA) e φstat(tA) che definiscono il primo spostamento si riferiscono all'errore dell'osservatore, vale a dire all'errore commesso dal compilatore del catalogo nella stima del piano dell'eclittica. Il secondo spostamento è definito dalla fluttuazione centenaria del piano dell'eclittica, che può essere calcolata dalla teoria di Newcomb.
Tutto quanto sopra implica anche il seguente corollario. Contrassegniamo con ΔBi(t) la discrepanza latitudinale della stella calcolata i per il momento presunto di osservazione t, mentre la stessa discrepanza per il momento t dopo la compensazione dell'errore sistematico, sarà descritta con
ΔBi0(t) = ΔBi(t) - γstat(t) sin(Li(t) + φstat(t)). Quindi, i valori di ΔBi0(t) dovranno essere indipendenti da t e pari agli errori casuali commessi da Tolomeo nella stima delle latitudini. La situazione cambia quando entrano nel gruppo stellare in fase di studio le stelle mobili, in quanto il loro valore di ΔBi0(t) dipende dal tempo t. La caratteristica della dipendenza è definita dai valori dei singoli errori casuali, come pure dalla direzione della velocità di moto proprio adeguate di tutte le stelle come se fossero viste contemporaneamente. In particolare, per l'epoca sconosciuta tA il valore di ΔBi0(tA) dovrà essere uguale all'errore casuale latitudinale per la stella i. Sarebbe naturale aspettarsi che se questa stella si muovesse abbastanza velocemente e allo stesso tempo sembri essere misurata bene, il valore di ΔBi0(t) dovrebbe raggiungere il suo minimo da qualche parte intorno al punto tA. La dimensione di questo intervallo minimo dipenderà dal valore e dalla velocità del moto proprio di una data stella e sarà uguale per centinaia di anni persino per le stelle più veloci: Arturo, per esempio.
La precedente considerazione e la Figura 5.5 hanno l'implicazione piuttosto importante che per poter determinare il polo PA dell'eclittica del catalogo eclittico si debba solo conoscere i due valori di γstat che corrisponderanno a due rispettivi valori del momento temporale t1 e t2.
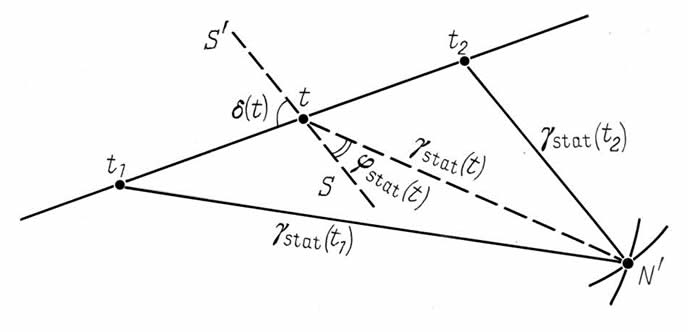
Figura 5.7.
Il calcolo dei valori γstat(t) e φstat(t).
In effetti, la teoria di Newcomb rende relativamente semplice determinare la velocità v del moto del polo dell'eclittica, vedere il Capitolo 1. Fissiamo i due momenti temporali t1 e t2 scelti arbitrariamente (vedere la Figura 5.7). Dobbiamo usare la formula 5.3.7 per calcolare i valori di γstat(t1) e γstat(t2). Ora disegniamo la linea del moto del polo dell'eclittica nel tempo, segnando anche i punti t1 e t2. La scala che sceglieremo dovrà anche fare in modo che la distanza tra i due punti sia pari a v|t2 - t1|. La posizione del polo PA dell'eclittica è determinata con il punto di intersezione delle due circonferenze i cui centri si trovano nei punti ti e i cui raggi sono uguali a γstat(ti), i = 1.2. La Figura 5.7 mostra come si calcolano i valori di γstat(t) e φstat(t) che corrispondono ai valori arbitrari di t. Questo angolo può anche essere calcolato con l'aiuto della teoria di Newcomb. Il significato astronomico della linea retta S'S è abbastanza ovvio: è la parte “raddrizzata” della grande circonferenza pertinente alla sfera celeste che attraversa il polo dell'eclittica P(t) dell'epoca t ed è perpendicolare (a P(t)) a un'altra grande circonferenza che attraversa anch'essa P(t) e il punto dell'equinozio dell'epoca t.
Analogamente, i calcoli dei parametri γstat(t) e φstat(t) per tutti i valori di t richiedono la conoscenza di due soli valori: φstat(t1) e φstat(t2).
Comunque sia, lavoreremo con l'angolo γ. È un valore conciso, in quanto è l'errore nella stima dell'angolo di inclinazione tra il piano equatoriale e il piano dell'eclittica. Facciamo notare che questo angolo può essere definito con l'uso della sfera armillare, per esempio. Perciò, l'errore γ inerente al valore di questo angolo può essere un errore strumentale della sfera armillare, vedere il Capitolo 1. Per cui, l'errore γ nasce naturalmente durante l'osservazione astronomica. A parte questo, la scelta di γ per la rappresentazione del parametro dovrà inoltre ricevere una convalida statistica.
5. Le proprietà statistiche delle stime di γstat e φstat.
Ora considereremo il problema del calcolo dei parametri γ e φ che definiscono l'errore sistematico del catalogo come un problema di matematica statistica. A questo scopo, ipotizziamo quanto segue: il compilatore del catalogo ha introdotto l'errore sistematico nel momento temporale tA; detto errore è definito dai parametri γA e φA. A parte questo, supponiamo che la latitudine di ciascuna stella misurata sia stata influenzata dalla perturbazione casuale ξi con una media dello zero come risultato dell'errore di osservazione, ossia E}ξi=0. Si presume che gli errori casuali ξi che corrispondono a stelle diverse, siano indipendenti e distribuiti uniformemente. Mettiamo che σ2= E}ξi2 rappresenti la dispersione del valore casuale ξi; in linea generale questa dispersione rimane a noi sconosciuta.
In queste presunzioni la latitudine della stella i assumerà la seguente forma:
Dal punto di vista statistico, ciò che abbiamo davanti è un campione composto da N realizzazioni di valori casuali {b1}Ni=1 della serie 5.5.1. Questo esempio deve essere utilizzato per il calcolo statistico dei parametri 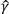 A e
A e 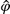 A di γA e φA, come pure per il calcolo del valore σ che è uguale all'equazione dell'errore medio quadratico. Dovremo localizzare immediatamente il problema e studiare le stime di
A di γA e φA, come pure per il calcolo del valore σ che è uguale all'equazione dell'errore medio quadratico. Dovremo localizzare immediatamente il problema e studiare le stime di 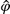 = φstat
= φstat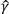 =γstat calcolate con il metodo dei minimi quadrati. Queste stime hanno la forma di 5.3.6 e 5.3.7. Gran parte della nostra attenzione deve essere rivolta verso la stima del valore γA per le ragioni spiegate alla fine del paragrafo 4.
=γstat calcolate con il metodo dei minimi quadrati. Queste stime hanno la forma di 5.3.6 e 5.3.7. Gran parte della nostra attenzione deve essere rivolta verso la stima del valore γA per le ragioni spiegate alla fine del paragrafo 4.
La Formula 5.5.1 sembra essere tradizionale per l'analisi di regressione. In effetti, questa equazione rivendica l'errore di osservazione Δbi = Bi(tA) - bi come un valore casuale con la media γA sin(Li(tA) + φA) a seconda dei parametri sconosciuti γA e φA e la dispersione σ2. Si devono stimare i valori dei parametri sconosciuti utilizzando il metodo dei minimi quadrati e determinare le qualità statistiche delle stime ricevute. A tali condizioni, la curva Y(x) = γA sin(x + φA) di solito viene indicata come la linea di regressione.
Definiamo i valori di γ e φ usando le relazioni espresse in 5.3.6 e 5.3.7. Per presunzione, le discrepanze Δbi sono casuali. Pertanto, anche le stime di φstat e γstat che otteniamo da queste formule sono dei valori casuali. Studiamo le loro qualità statistiche e consideriamo la loro relazione con gli effettivi valori sconosciuti di φA e γA.
Eseguiamo la sostituzione di sb e cb nelle formule descritte sopra, usando la differenza γA sin(Li(tA) + φA) - ξi al posto di Δbi e applicare detta sostituzione alle formule 5.3.6 e 5.3.7. Finiremo con le seguenti espressioni per i valori φstat e γstat.
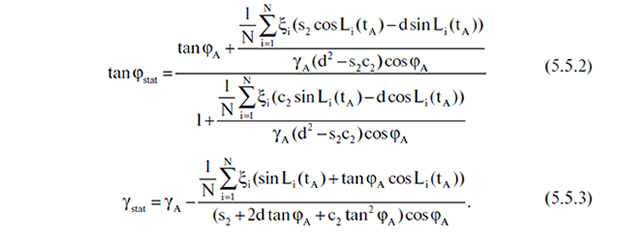
Introduciamo il valore
R=(γA(d2 - s2c2)cos φA)-1.
In questo caso 5.5.2 può essere trascritta con
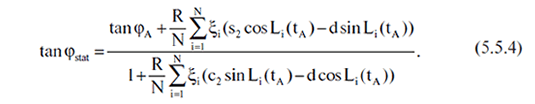
La condizione Εξi = 0 ci dice che la stima del parametro γstat ricevuta non si è spostata, ovvero:
Eγstat = γA. (5.5.5)
La dispersione per la stima di γstat espressa attraverso Dγ sembra una cosa così:
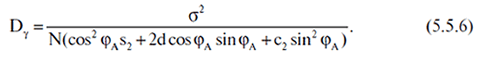
Se gli errori di osservazione ξi sono distribuiti normalmente, lo stesso vale per il valore γstat e i primi due momenti (5.5.5 e 5.5.6) definiscono tutta la sua distribuzione. Questo fatto ci darà l'opportunità di costruire un intervallo di confidenza per il valore di γA.
L'analisi della stima di φstat è un po' più complessa. Usiamo l'equazione resa dalla formula 5.5.4:
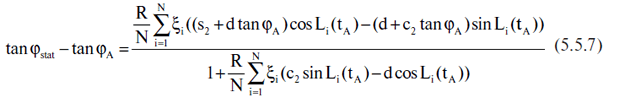
così come il fatto che per I grandi valori di N, il secondo oggetto nel denominatore della parte destra di 5.5.7 è un piccolo valore. Questo valore è davvero di natura casuale, con una media nulla e una dispersione di
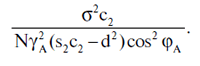
Se i valori di ξi sono distribuiti normalmente, lo stesso vale per il valore in esame. Per l'Almagesto ha le seguenti implicazioni: persino per N = 30 la probabilità PN che il denominatore della parte destra di 5.5.7 possa essere negativo non supera 5 × 10–3. Questa probabilità diminuisce drasticamente con la crescita di N: P50 ≤ 2,5 × 10–4, P80≤ 4 × 10–6, P100≤ 3 × 10–7, P200≤ 8 × 10–13, P300≤ 2,5 × 10–8.
In linea generale la formula 5.5.7 implica che Ε tan φstat ≠ tanφA. Tuttavia, possiamo facilmente ottenere la funzione di distribuzione F(x) del valore casuale tan φstat - tan φAda questa formula di cui abbiamo bisogno per stimare l'intervallo di confidenza per φA. Infatti, se dovessimo ignorare il caso piuttosto improbabile del denominatore che in 5.5.7 diventa negativo, potremmo estrarre l'espressione F(x) da questa formula:
F(x) = P(tan φstat - tan φA <x) = P(ηx - x),
dove il valore casuale ηx ha la forma di


Figura 5.8.
Una pagina dall’edizione del 1551 dell’Almagesto.
Pertanto, se i valori di ξi sono distribuiti normalmente con una dispersione pari a σ2, il valore ηx avrà una distribuzione gaussiana con la media nulla e la dispersione di

Per cui,

dove
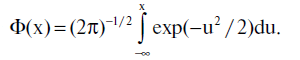
I valori di γstat e φstat calcolati sopra sono le cosiddette stime puntuali dei parametri sconosciuti γA e φA. Dal momento che abbiamo trovato le funzioni di distribuzione per queste stime, possiamo studiare il problema dei possibili errori inerenti. Rispondiamo a questa domanda nei termini standard utilizzati per gli intervalli di confidenza basati sulle formule 5.5.5, 5.5.6, 5.5.8 e 5.5.9.
In matematica statistica il problema del calcolo dell'intervallo di confidenza dipende dalla seguente situazione che illustriamo con l'esempio della stima del valore γA. Questo valore è un errore deterministico di una certa natura commesso dal compilatore del catalogo. Come risultato della stima statistica di γA, nel nostro caso con l'aiuto del metodo dei minimi quadrati, arriviamo al valore casuale γstat. Se fossimo già riusciti a determinare γstat, ci si potrebbe chiedere quali siano i confini del valore sconosciuto γA.
Per evitare che questi confini diventino banali, dobbiamo definire un tasso accettabile di errore delle probabilità, cioè quelle probabilità di specificare quei confini che non devono contenere il valore effettivo di γA. Usiamo ε per riferirci al tasso accettabile di errore delle probabilità. In tal caso, il livello di confidenza dovrà essere 1 - ε. Il valore casuale di γstat è distribuito normalmente con i parametri definiti dalle formule 5.5.5 e 5.5.6. Pertanto, per x > 0 avremo

Definiamo il valore di (ε/2), i frattili della distribuzione normale xε dall'equazione:

o in alternativa un'altra equazione che dia lo stesso risultato 
Per cui l’intervallo
Iγ(ε) = (γstat - xε, γstat + xε) (5.5.10)
rappresenta l'intervallo di confidenza per γA con un livello di confidenza pari a 1 - ε. Questo segue da P(|γstat -γA| ≥ xε) = ε.
Quando proviamo a calcolare il valore di xε, dobbiamo appoggiarci in particolare al valore Dγ, che dipende dai parametri sconosciuti σ2 e φA. Come si fa di solito in matematica statistica, nella formula sostituiremo σ2 con Dγ per mezzo della dispersione residuale
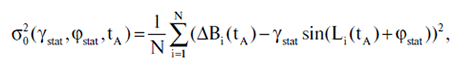
definita dalla formula 5.5.3 e da φA per mezzo di φstat. Anche il momento tA della compilazione del catalogo resta a noi sconosciuto; pertanto, tutti i calcoli sopra elencati devono essere effettuati per tutti i momenti t, al fine di poter stimare l'errore sistematico γstat(t), φstat(t), ipotizzando che il catalogo sia stato compilato nell'epoca casuale e fissa t.
Allo stesso modo possiamo estrarre l'intervallo di confidenza per φA con il livello di confidenza 1 - ε. Questo intervallo Iφ(ε) assomiglierà a quanto segue:

yε è la soluzione dell'equazione F(y) - F(–yε) =1 - ε, dove la funzione della distribuzione F viene definita dall'uguaglianza di 5.5.9, cioè ε/2, il frattile della corrispondente distribuzione normale.
Nota: le stime riportate dei tassi degli errori effettivi per γ e φ nel catalogo, come le funzioni della datazione presunta, non sono solo importanti perché siamo in grado di compensarli, ma anche per la verifica indiretta di quanto sembri essere corretto l'approccio suggerito. Ad esempio, se arrivassimo a un valore di γstat che fosse molte volte maggiore al tasso di precisione del catalogo, starebbe a indicare l'esistenza di effetti sostanziali che non abbiamo preso in considerazione.
Tuttavia, per quanto riguarda la datazione stessa,il valore effettivo di γstat non prende parte alla corrispondente procedura. Tutto quello che dobbiamo sapere è la lunghezza del rispettivo intervallo di confidenza. Pertanto, si potrebbero semplificare di molto i calcoli come segue. Per esempio, si deve calcolare γstat e φstat per qualsiasi momento fisso nel tempo t0: 1900 d.C., il che non renderebbe necessari i calcoli di Newcomb. Quindi, al posto delle curve γstat(t) e φstat(t) avremo i valori costanti corrispondenti agli errori di osservazione; tuttavia, il sistema delle coordinate sarà pertinente all'epoca del 1900 d.C. Quindi tracceremo gli intervalli di confidenza attorno a questi valori costanti la cui lunghezza non dipenderà da t. Se effettuassimo la procedura statistica di datazione descritta di seguito, dovremmo finire con lo stesso intervallo della possibile datazione del catalogo a cui siamo arrivati nella stima degli errori γ e φ per la presunta epoca di datazione t. Le sole informazioni che perderemo saranno i valori effettivi stimati di γstat e φstat.
6. Corollari.
Corollario 1. L'errore di gruppo della configurazione stellare risulta in detta configurazione dallo spostamento sulla sfera celeste. Questo spostamento potrebbe essere parametrizzato dai due parametri γ e φ (o γ; e β), qualora dovessimo considerare esclusivamente le discrepanze latitudinali.
Corollario 2. Di conseguenza, le discrepanze latitudinali inerenti al catalogo possono essere ridotte compensando gli errori di gruppo.
Corollario 3. Se gli errori di gruppo coincidessero per buona parte del catalogo, questo errore comune si chiamerebbe sistematico e potrebbe essere trovato con i metodi della matematica statistica. A condizione che l'epoca di compilazione del catalogo sia uguale a t, i valori dei parametri φ(t) e γ(t) potrebbero essere facilmente valutati con il metodo dei minimi quadrati. Le corrispondenti stime di γstat(t) e φstat(t) avranno le rispettive forme di 5.3.6 e 5.3.7.
Corollario 4. È sufficiente conoscere i valori di γstat(t1) e γstat(t2) per due diversi momenti nel tempo, per poter ricostruire le funzioni γstat(t) e φstat(t).
Corollario 5. Gli intervalli di confidenza Iφ(ε) e Iγ(ε) per i valori effettivi dei parametri φ(t) e γ(t) sono stati calcolati in base all'ipotesi che gli errori casuali si siano distribuiti normalmente. Vedi le rispettive formule 5.5.11 e 5.5.10.
Concludiamo riportando una pagina dell'edizione del 1551 dell'Almagesto, vedi la Figura 5.8.