CAPITOLO 6
Le proprietà statistiche e di precisione del catalogo dell’Almagesto
1. Note introduttive.
Nei capitoli precedenti abbiamo stimato che uno dei problemi principali per la datazione dell'Almagesto tramite i moti propri delle stelle è rappresentato dall'effettiva precisione delle latitudini stellari del catalogo dell'Almagesto per le diverse regioni celesti. Pertanto, è necessario condurre un'analisi meticolosa degli errori nelle coordinate stellari del catalogo in generale e nelle sue varie parti. E' già stata condotta un'analisi preliminare e piuttosto approssimativa (vedi Capitoli 2 e 4).
Lo strumento principale di questo capitolo include i metodi per il calcolo degli errori sistematici nelle coordinate stellari, come descritti nel Capitolo 5. Prima di tutto, dimostreremo che le sette regioni dell'atlante stellare dell'Almagesto descritte in precedenza differiscono effettivamente tra loro per il tasso degli errori sistematici, come anche per gli errori casuali di misurazione. Troveremo gli errori nella stima del polo dell'eclittica anche per ciascuna di queste aree, come pure i valori della media quadratica residuale relativi agli errori nelle coordinate stellari. Inoltre, creeremo gli intervalli di confidenza dei parametri degli errori sistematici γstat e φstat per ciascuna delle aree.
Successivamente analizzeremo alcune aree celesti relativamente piccole: le costellazioni e i dintorni delle singole stelle. L'obiettivo di questa analisi è assicurarsi che i valori scoperti di γstat e φstat possiedono di fatto la natura degli errori sistematici presenti nelle parti sostanziali del catalogo dell'Almagesto e non sono affatto il semplice risultato di numerosi errori di gruppo sovrapposti gli uni sugli altri e che differiscono da uno piccolo gruppo di stelle a un altro.
Di conseguenza, calcoleremo l'area della sfera celeste che è stata misurata abbastanza bene da Tolomeo. A dire il vero si è rivelata piuttosto significativa. La nostra datazione dell'Almagesto si baserà proprio sulle coordinate stellari di quest'area, quella in cui i calcoli di Tolomeo si dimostrarono i più precisi.
2. Le sette regioni della sfera celeste.
2.1. La caratteristica delle sette aree che abbiamo scoperto nell’atlante dell’Almagesto.
Nel Capitolo 2 abbiamo descritto le sette aree in cui può essere divisa la sfera celeste; si manifestano anche nel catalogo dell'Almagesto, vedere la Figura 6.1.
In questo capitolo analizziamo le coordinate di Tolomeo per un totale di 864 stelle. Queste 864 stelle erano quelle che poi, a seguito di una filtrazione, sono diventate le 100 stelle dell'Almagesto. In primo luogo, sono state rimosse le cosiddette stelle informata per i motivi considerati nel Capitolo 2, per cui non sono state incluse nelle costellazioni canoniche. In secondo luogo abbiamo filtrato anche i “refusi” e le stelle identificate in modo ambiguo. La Tabella 6.1 contiene le indicazioni precise riguardanti le stelle dell'Almagesto incluse in una determinata regione e la quantità residuale di stelle dopo la “filtrazione” di ogni area. In questa tabella abbiamo usato la numerazione di Bailey, ossia i numeri delle stelle presi dal catalogo dell'Almagesto.

Figura 6.1.
. Le sette aree che abbiamo scoperto nella carta stellare dell'Almagesto.
Le stelle con nome sono raffigurate dai puntini neri.
Prendiamo in considerazione la Figura 6.1 che rappresenta la divisione della sfera celeste nelle regioni sopracitate. Tutte le 12 stelle con nome dell'Almagesto sono state contrassegnate con dei punti neri. È facile vedere che il contorno dell'area A è stato chiaramente definito dalle stelle con nome. Si ha l'impressione che Tolomeo attribuì un significato speciale all'area celeste A. Anche questo è stato confermato dalla nostra analisi preliminare nel Capitolo 2. Come vedremo di seguito, l'area A risulta essere la più importante per il nostro studio sulla datazione. Occorre anche far notare che l'area in questione contiene il polo celeste (contrassegnato con N) e il polo dell'eclittica (contrassegnato con P).
Le stelle con nome che circondano l'area A devono essere servite a Tolomeo come una sorta di base mentre stava eseguendo le sue osservazioni. Si riferiva a loro quando si spostava ulteriormente verso il centro dell'area A per misurare le coordinate di tutte le altre stelle. Come si spostava da una stella a un'altra, gli errori di misurazione si accumulavano. Ci si dovrebbe quindi aspettare che le stelle della regione A che si trovano fuori dallo Zodiaco siano state in linea generale misurate peggio delle stelle zodiacali. La metà delle stelle con nome dell'Almagesto (6 su 12) o fanno parte dello Zodiaco, o sono situate nelle sue immediate vicinanze. Lo Zodiaco include Regolo, Spiga, Antares, Previndemiatrix e Aselli. Procione è proprio accanto allo Zodiaco.
Tabella 6.1. La distribuzione delle stelle dell'Almagesto attraverso le aree celesti, specificando quante stelle sono rimaste in ciascuna delle aree dopo la filtrazione del catalogo. Abbiamo usato la numerazione di Bailey, ossia i numeri delle stelle come specificati nel catalogo dell'Almagesto |
||
Le regioni della sfera celeste nell’Almagesto |
La numerazione di Bailey della regione prima e dopo la filtrazione del catalogo |
|
prima |
dopo |
|
A |
1-158 e 424-569 |
249 |
B |
286-423 e 570-711 |
262 |
C |
847-977 |
116 |
D |
712-846 e 998-1028 |
143 |
M |
159-285 |
94 |
Zod A |
424-569 |
124 |
Zod B |
362-423 e 570-711 |
168 |
2.2. La disposizione dei poli dell’eclittica per ciascuna delle sette regioni dell’atlante stellare dell’Almagesto.
Individuiamo innanzitutto la disposizione dei poli dell'eclittica per ciascuna delle sette regioni celesti dell'Almagesto. Nel Capitolo 5 abbiamo dimostrato che la posizione dei poli dell'eclittica rispetto al catalogo stellare sono definite dai parametri γstat e φstat. Questi parametri sono stati stimati dal catalogo attraverso l'applicazione del metodo dei minimi quadrati in conformità con le formule (5.3.6 e 5.3.7).
Calcoliamo separatamente i valori dei parametri γstat e φstat. per ciascuna delle sette regioni celesti. Successivamente contrassegneremo ciascuna posizione corrispondente al polo dell'eclittica, vedere la Figura 6.2. Nella stessa illustrazione abbiamo anche definito il moto del polo dell'eclittica effettiva P(t), che corrisponde alle variazioni della presunta datazione.
Nella Figura 6.2 abbiamo usato come esempio il seguente segmento: collega il polo dell'eclittica per l'area celeste B con il polo dell'eclittica effettiva per l'epoca t = 10 contrassegnato con P(10). La lunghezza di questo segmento è uguale a γBstat (10). L'angolo tra questo segmento e la retta che sta per l'arco D(10) D'(10), la cui definizione è stata riportata nelle Figure 5.4 e 5.5, ha un valore pari a γBstat (10). Ovviamente, per t può essere presa qualsiasi altra epoca, idem per l'area B, mentre i rispettivi valori di γstat e φstat possono essere dedotti con l'aiuto della Figura 6.2.
La Tabella 6.2 contiene i valori di γstat(18) e φstat(18) che abbiamo calcolato per ciascuna delle sette regioni celesti. Queste posizioni forniscono una chiara definizione del “polo dell'eclittica dell'osservatore” per ciascuna delle aree. Tuttavia, potremmo altrettanto facilmente prendere qualsiasi altra coppia di valori γstat e φstat per il valore casuale di t. Vi rimandiamo ancora al paragrafo 5.4. A parte ciò, la Tabella 6.2 contiene i valori di σinit (18) e la media quadratica residuale di σmin delle discrepanze latitudinali risultanti dalla compensazione dell'errore sistematico (vedere le formule 5.3.2 e 5.3.3). Nel paragrafo 5.4 dimostriamo che qualora ignorassimo l'influenza inconsistente del moto proprio della stella, σmin non dipenderebbe dal momento temporale t preso in considerazione. Pertanto, σmin viene definito esclusivamente dal polo dell'eclittica, che per questo gruppo di stelle dell'Almagesto può essere stimato statisticamente.
Per quanto riguarda il moto proprio delle stelle, va fatto notare che influenza difficilmente sia l'errore sistematico stimato γstat(t), φstat(t), che la discrepanza residuale media quadratica delle coordinate stellari del catalogo dell'Almagesto. Pertanto possiamo omettere tutti i riferimenti relativi all'effetto del moto proprio, anche se nei nostri calcoli sarà ovviamente sempre preso in considerazione.

Figura 6.2.
La rispettiva disposizione del polo dell'eclittica mobile P(t) e i poli dell'eclittica stimati per ciascuna delle sette parti comprese nel catalogo dell'Almagesto.
Per la Tabella 6.2 abbiamo scelto il valore di t = 18, solo perché questo momento corrisponde alla datazione di Scaligero dell'Almagesto.
Tabella 6.2. I valori calcolati dei parametri di errore γstat(18) e φstat(18) specificati nell'Almagesto per le diverse regioni celesti. |
|||||||
Caratteristiche |
Le aree della sfera celeste dell’Almagesto |
||||||
A |
B |
C |
D |
M |
Zod A |
Zod B |
|
γstat(18) |
18.5 |
13.6 |
9.7 |
26.6 |
19.4 |
16.4 |
20.0 |
φstat(18) |
34.0 |
-34.5 |
-122.5 |
-52.7 |
-50.5 |
-21.7 |
-23.5 |
σinit(18) |
20.5 |
21.8 |
23.4 |
27.3 |
23.0 |
17.7 |
24.0 |
σmin |
16.5 |
19.2 |
22.5 |
24.4 |
20.5 |
12.8 |
19.3 |
Pini(18),in % |
36.5 |
35.5 |
33.6 |
28.7 |
37.2 |
30.6 |
30.9 |
Pmin, in % |
50.6 |
43.5 |
43.1 |
35.7 |
45.7 |
63.7 |
44.0 |
Inoltre, la Tabella 6.2 contiene la caratteristica statistica della precisione stellare delle coordinate dell'Almagesto. Il valore di Pinit(18) corrisponde alla percentuale delle stelle la cui discrepanza latitudinale non supera i 10' per la datazione del 100 d.C. (t = 18), dove 10' è la misura della scala minima del catalogo dell'Almagesto. Il valore di Pmin corrisponde alla quota delle stelle la cui discrepanza latitudinale non supera i 10' dopo la compensazione dell'errore sistematico. Questo valore viene difficilmente influenzato dalla datazione delle osservazioni per le grandi quantità di stelle prese ora in considerazione.
La disposizione dei poli dell'Almagesto definibili statisticamente, mostrati nella Figura 6.2 in relazione alla traiettoria del moto del polo effettivo, ci dice che in ogni area celeste eccetto la C, l'errore sistematico del catalogo dell'Almagesto lo rende “più antico” persino rispetto all'epoca di Ipparco.
Ricordiamo ai lettori che l'errore sistematico minimo nella regione celeste C cade in t ~ 10, ovvero nell'anno ~ 900 (900 d.C.). Tuttavia, come abbiamo menzionato sopra la disposizione del polo della “Eclittica di Tolomeo” non è in nessun modo correlato alla data di compilazione del catalogo. Questa disposizione ci dice semplicemente il carattere e il valore dell'errore sistematico commesso da Tolomeo nelle misurazioni delle coordinate stellari condotte per le varie regioni celesti.
Un'altra implicazione fatta per mezzo della Figura 6.2 è che le posizioni del polo stimate statisticamente per le regioni A, ZodA e ZodB, sono piuttosto vicini tra loro. In altre parole, pare che Tolomeo abbia commesso lo stesso errore sistematico per ciascuna di queste regioni celesti. Torneremo su questo fatto più avanti, durante la nostra analisi delle singole costellazioni dell'Almagesto. Inoltre, come si può vedere dalla Figura 6.2, il polo dell'eclittica definito dalla regione B del catalogo dell'Almagesto si trova anche accanto al polo dei gruppi A, ZodA e ZodB. Il polo dell'area M si trova più lontano e quello dell'area D ancora di più. A quanto pare, l'errore sistematico delle aree di M e D dell'Almagesto ha un valore diverso da quello dell'area ZodA. Nella Figura 6.2, l'area C sembra proprio essere un “refuso”.
2.3. Il calcolo degli intervalli di confidenza
Nella paragrafo precedente abbiamo calcolato discrete stime statistiche di γstat e φstat per i parametri sconosciuti (γ e φ) dell'errore sistematico nel catalogo dell'Almagesto. Nel paragrafo 5.5 abbiamo già ricordato ai lettori la definizione di intervallo di confidenza. Di seguito riportiamo la risultante rappresentazione visiva. Innanzitutto costruiremo dei grafici di dipendenza per t e le stime di γstat(t) e φstat(t), dove 1 ≤ t ≤ 25. Quindi disegneremo delle strisce sui grafici risultanti, le cui sezioni verticali saranno gli intervalli di confidenza Iγ(ε) e Iφ(ε) con il livello di confidenza ε = 0.1. Gli intervalli di confidenza saranno calcolati in conformità con le formule 5.5.10 e 5.5.11.
Iγ(ε) = (γstat - xε, γstat + xε) (5.5.10)

Il risultato di questi calcoli può essere visto nelle Figure dalla 6.3 alla 6.9. Nella Tabella 6.3 potete trovare i molti dati sui confini dei diversi livelli ε di confidenza e i due valori della presunta datazione de catalogo dell'Almagesto (t = 7, ossia 1200 d.C.; t = 18, ossia 100 d.C.). Questa tabella contiene i valori della metà degli intervalli di confidenza Iγ(ε). Ricordiamo ai lettori che il centro dell'intervallo di confidenza per γ e ogni valore fisso di t sono la stima di γstat(t) senza alcun spostamento, vedi il paragrafo 5.5.
In linea di massima, l'intervallo di confidenza Iφ(ε) per φ è asimmetrico rispetto a φstat(t), dal momento che questa stima potrebbe spostarsi. Tuttavia, la sopracitata asimmetria è abbastanza insignificante e quindi si può considerare che φstat(t) è il centro approssimativo dell'intervallo di confidenza. indica la semi-larghezza dell'intervallo Iγ(ε), mentre la semi-larghezza dell'intervallo Iφ(ε).
Le cifre che si trovano nelle Tabelle 6.2 e 6.3 implicano ciò che segue. La zona ZodA dell'Almagesto è la regione celeste misurata più accuratamente. Questo è ovvio dal fatto che la compensazione dell'errore sistematico scoperto per questo gruppo di stelle consente di ridurre l'errore medio quadratico a 12,8'. Inoltre, si è scoperto che il 64% delle stelle è finito con una discrepanza latitudinale inferiore a 10'.
Il secondo gruppo di stelle più preciso appartiene alla zona A dell'Almagesto, dove la discrepanza latitudinale media quadratica è stata ridotta a 16,5' dopo la compensazione dell'errore sistematico. In questa regione la quota delle stelle la cui discrepanza latitudinale è inferiore a 10' è cresciuta di oltre il 50%.
| Tabella 6.3. I valori della semi-larghezza dell'intervallo di confidenza Iγ(ε) e della semi-larghezza dell'intervallo di confidenza Iϕ(ε) per i diversi livelli di confidenza di ε e le due datazioni presunte del catalogo dell'Almagesto: il 1200 d.C. (t = 7) e il 100 d.C. (t = 18). |
|||||||||
| 1200 d.C. | 100 d.C. | ||||||||
| Area ↓ | ε → | 0.1 | 0.05 | 0.01 | 0.005 | 0.1 | 0.05 | 0.01 | 0.005 |
| A | xεγ | 2.6 | 3.1 | 4.1 | 4.5 | 2.7 | 3.2 | 4.2 | 4.6 |
| xεφ | 11.7 | 14.0 | 18.3 | 20.0 | 16.6 | 19.8 | 25.9 | 28.4 | |
| B | xεγ | 2.7 | 3.2 | 4.2 | 4.6 | 2.6 | 3.4 | 4.0 | 4.4 |
| xεφ | 14.7 | 17.4 | 22.8 | 25.0 | 22.1 | 26.2 | 34.4 | 37.6 | |
| C | xεγ | 4.6 | 5.5 | 7.2 | 7.9 | 5.1 | 6.0 | 7.9 | 8.7 |
| xεφ | 91.1 | 108.2 | 141.9 | 155.2 | 60.7 | 72.2 | 94.7 | 103.5 | |
| D | xεγ | 6.3 | 7.4 | 9.8 | 10.7 | 7.2 | 8.6 | 11.3 | 12.3 |
| xεφ | 28.3 | 33.6 | 44.1 | 48.2 | 37.8 | 44.9 | 58.9 | 64.4 | |
| M | xεγ | 5.4 | 6.4 | 8.5 | 9.2 | 6.5 | 7.7 | 10.1 | 11.0 |
| xεφ | 28.2 | 33.5 | 43.9 | 48.0 | 42.4 | 50.3 | 66.0 | 72.2 | |
| Zod A | xεγ | 2.5 | 2.9 | 3.9 | 4.2 | 2.5 | 3.0 | 4.0 | 4.3 |
| xεφ | 11.4 | 13.6 | 17.8 | 19.5 | 18.1 | 21.5 | 28.2 | 30.8 | |
| Zod B | xεγ | 3.5 | 4.2 | 5.5 | 6.0 | 3.4 | 4.1 | 5.4 | 5.9 |
| xεφ | 14.3 | 17.0 | 22.3 | 24.4 | 19.8 | 23.5 | 30.8 | 33.7 | |
 Figura 6.3. Il comportamento degli errori sistematici γstat(t), φstat(t) e βstat(t) per la regione celeste A dell'Almagesto. |
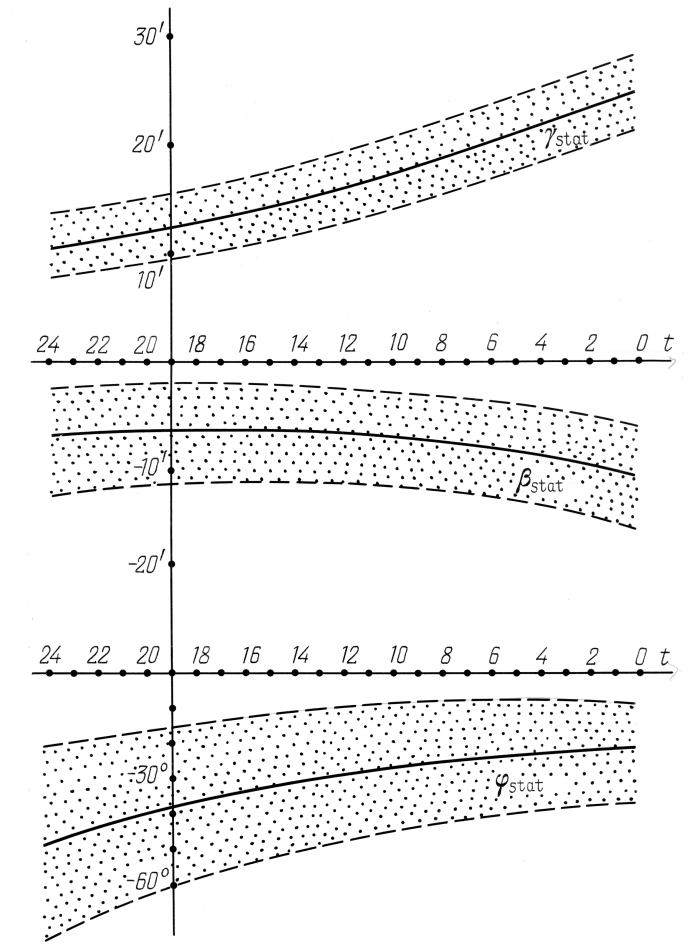 Figura 6.4. . Il comportamento degli errori sistematici γstat(t), φstat(t) e βstat(t) per la regione celeste B dell'Almagesto. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
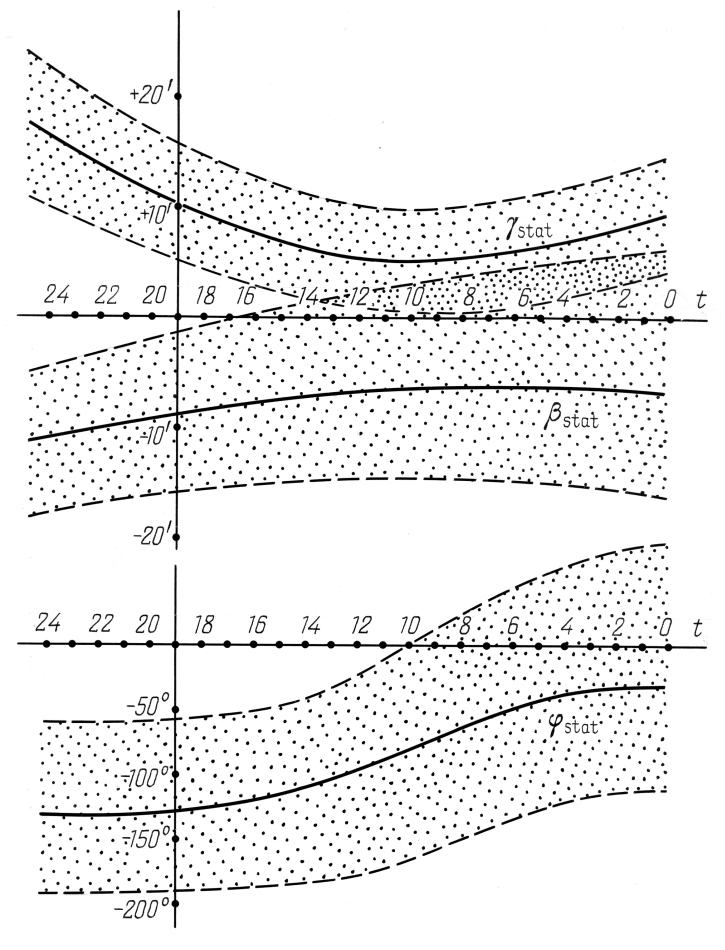 Figura 6.5. Il comportamento degli errori sistematici γstat(t), φstat(t) e βstat(t) per la regione celeste C dell'Almagesto. |
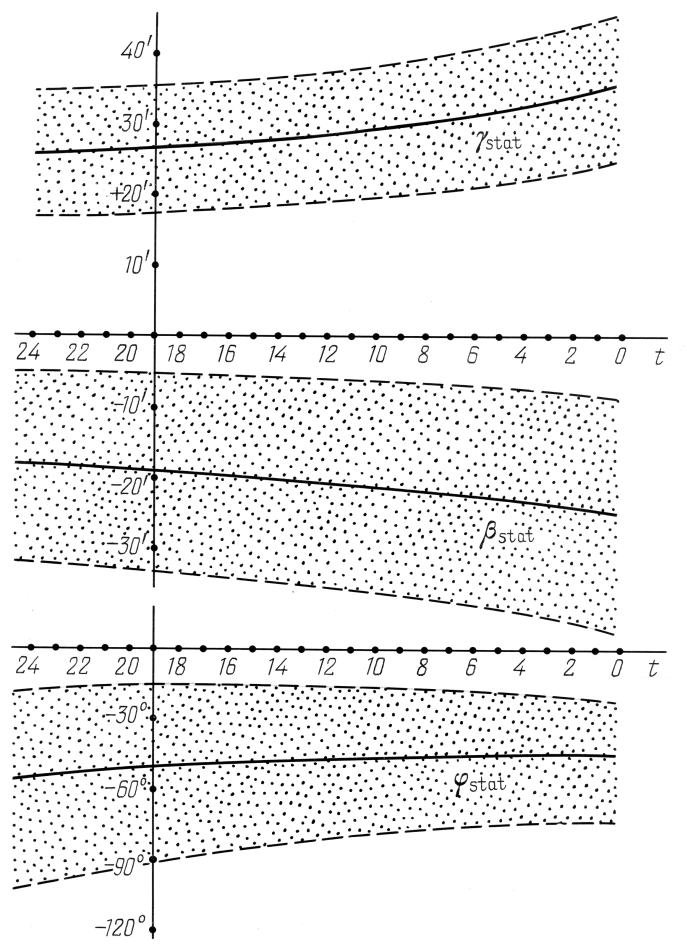 Figura 6.6. Il comportamento degli errori sistematici γstat(t), φstat(t) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
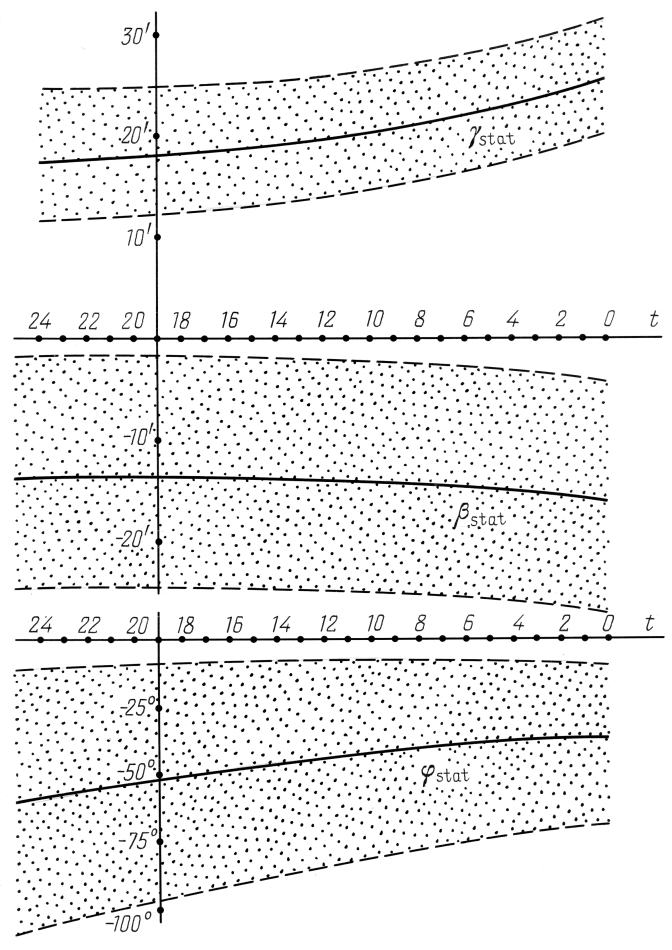 Figura 6.7. Il comportamento degli errori sistematici γstat(t), φstat(t) |
 Figura 6.8. Il comportamento degli errori sistematici γstat(t), φstat(t) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
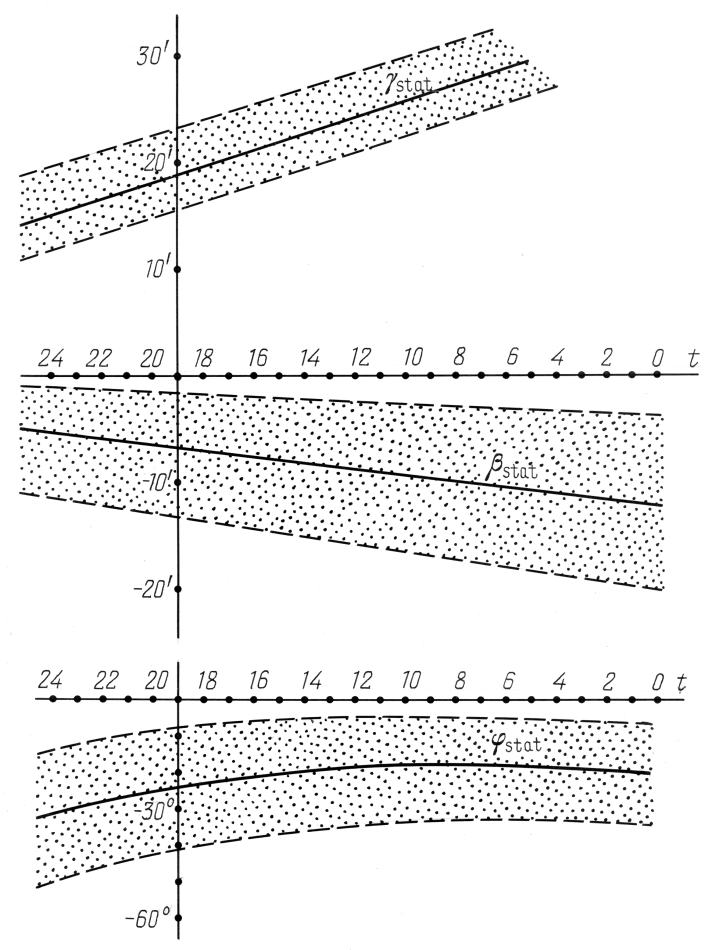 Figura 6.9. Il comportamento degli errori sistematici γstat(t), φstat(t) e βstat(t) per la regione celeste ZodB dell'Almagesto. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Gli intervalli di confidenza Iγ(ε) e Iφ(ε) per le regioni celesti ZodA e A si sono rivelate di dimensioni simili, vedere la Tabella 6.3, sebbene la precisione delle misurazioni sia maggiore nell'area ZodA. Ciò è spiegato dalla quantità eterogenea di stelle in queste parti. Meno sono le stelle, maggiore è la dimensione dell'intervallo di confidenza; quest'ultimo viene ridotto da una maggiore precisione nella misurazione.
I dati della Tabella 6.2 confermano la precisione di 10' dichiarata da Tolomeo almeno per quanto riguarda le latitudini stellari.
I prossimi gruppi di stelle misurati meglio nell'Almagesto sono concentrati nelle aree B e ZodB. Le loro caratteristiche di precisione sono piuttosto vicine tra loro. L'errore medio quadratico residuale è approssimativamente uguale a 19'. Le stelle con una discrepanza latitudinale sotto i 10' costituiscono il 44% di questi gruppi. A prima vista, le posizioni del polo dell'eclittica calcolate per queste parti del cielo dell'Almagesto sembrano essere vicine alle posizioni dei poli delle aree A e ZodA; tuttavia, vanno a finire nei rispettivi intervalli di confidenza solo con dei valori sufficientemente piccoli di ε ≈ 0,01, il che significa che gli errori sistematici delle aree celesti B e ZodB possono differire da quelli di A e ZodA. Inoltre, le stelle nelle aree A e ZodA sono state misurate sostanzialmente con maggiore precisione rispetto a quelle nelle aree B e ZodB. Di seguito riportiamo ulteriori prove a testimonianza di quanto detto.
Le stelle nelle aree C, D e M sono state misurate peggio di quelle nelle aree A e B. Inoltre, i valori delle stime di γstat e φstat finiscono negli intervalli di confidenza delle aree A, ZodA, B e ZodB solo quando i valori di ε sono davvero molto piccoli, il che significa che dobbiamo consentire l'esistenza di errori sistematici nelle aree C, D e M che differiscono dagli errori sistematici pertinenti alle regioni celesti A, ZodA, B e ZodB.
L'analisi delle Tabelle 6.2 e 6.3 ci ha già fatto riflettere sui valori dell'errore medio quadratico che si dovrebbero considerare grandi e piccoli. Facciamo riferimento all'analisi della sensibilità descritta nel Capitolo 5. Lo schema della soluzione può essere visto nella Figura 6.10.

Figura 6.1.
La stima delle variazioni ammissibili nei valori della discrepanza latitudinale media quadratica.
Disegniamo le curve ellissoidali del livello della funzione σ2 (γ, φ, t) sul piano delle coordinate (γ, φ) secondo la formula 5.3.9. Sullo stesso piano disegniamo il rettangolo R(ε), con le proiezioni delle coordinate Iγ(ε) e Iφ(ε). Si tratta del rettangolo ombreggiato nella Figura 6.10. In questo caso, la probabilità che il valore effettivo dell'errore sistematico (γ, φ) si trovi all'interno di questo rettangolo, è di 1 - 2ε o persino superiore. Troviamo σ2max (ε), dove viene preso il valore massimo per ciascuna delle coppie (γ, φ) ∈R(ε). Il valore risultante di σmax(ε) definisce la discrepanza media quadratica consentita con un livello di confidenza di 1 - 2ε, sebbene la differenza di σmax(ε) - σmin definisca l'espansione consentita della discrepanza media quadratica dovuta alla mancanza di una sufficiente precisione nella stima dei parametri γ e φ tramite i valori di γstat e φstat.
La Tabella 6.4 contiene i valori di a11, a12, a22 per le aree celesti A e ZodA per il momento temporale di t = 18; definiscono le curve di livello dell'errore medio quadratico. Queste curve di livello sono state calcolate con l'aiuto della formula 5.3, che prevede la misurazione di γ in gradi d'arco e φ in gradi. La tabella contiene anche i valori di Δσ = σmax(ε) - σmin calcolati per i valori “estremi” ε = 0,1 e ε = 0,005. Va detto che i valori risultanti sembrano cambiare leggermente con il tempo. Queste cifre dimostrano l'ovvia divisione di precisione tra le aree A e ZodA da una parte, e B e ZodB dall'altra. Anzi, anche con il livello di confidenza di 1 - 2ε = 0,99, il valore dell'errore medio quadratico dell'area di confidenza costruita per la regione ZodA, rimane inferiore al valore minimo dell'errore per le regioni celesti B e ZodB.
Un'affermazione simile deve essere valida anche per la regione celeste A. Sebbene il valore σAmax della regione A sia maggiore di σBmax, questo vale solo per ε ≤ 0,01. Gli altri valori creano dei livelli di errore nelle regioni celesti A e B sostanzialmente diversi o separati da un criterio statistico. Si deve aggiungere che le stelle nel gruppo ZodA sono altrettanto diverse dalle loro controparti del gruppo, poiché per tutti i valori considerati di ε, il valore di σmax trovato in ZodA è inferiore al valore di σmin calcolato per la regione A.
Inoltre, la Tabella 6.3 dimostra che il parametro φstat non può essere calcolato con sufficiente precisione, specialmente per le regioni di “scarsa qualità” C, D e M. Ciò viene confermato dalle dimensioni degli intervalli di confidenza Iφ(ε). Ad esempio, l'intero raggio di questo intervallo supera i 180 gradi nel caso dell'area C.