CAPITOLO 6
Le proprietà statistiche e di precisione del catalogo dell’Almagesto
3. La nostra analisi delle singole costellazioni dell’Almagesto.
3.1. Il compilatore dell’Almagesto potrebbe avere commesso un errore diverso nel caso di ogni gruppo minore di costellazioni.
Sono necessarie ulteriori analisi a causa del seguente problema. I parametri γstat e φstat che definiscono l'errore sistematico, sono stati trovati in alcuni grandi gruppi di stelle. Corrispondono allo spostamento dell'eclittica che minimizza la discrepanza media quadratica per le stelle contenute in questo gruppo. Tuttavia, non si deve escludere a priori la possibilità che il compilatore abbia fatto un gruppo diverso di errori nel caso di ogni piccolo gruppo stellare, tipo una singola costellazione. In questo caso, i parametri γstat e φstat non sono delle medie significative dell’effettivo errore di gruppo e per questo motivo ci saranno di scarsa utilità.
Dobbiamo far notare che le dimensioni degli intervalli di confidenza per i valori di φstat trovati nel paragrafo 2 sono piuttosto sostanziali. Questo può essere spiegato dalla bassa sensibilità delle discrepanze latitudinali nella rotazione dell'angolo φ e dalla natura “non sistematica” dell'errore φstat. In altre parole, è possibile che i parametri γstat e φstat abbiano una natura diversa, vale a dire che γstat è il risultato dell'errore di un osservatore che influenza tutte le stelle (un errore nella stima della posizione dell'eclittica), mentre φstat è il valore medio di numerosi singoli errori. Tale differenza nel comportamento dei parametri è facile da spiegare, se si considera lo strumento astronomico principale dell'epoca dell'Almagesto, per esempio la sfera armillare (vedi Capitolo 1). L'angolo tra il piano dell'eclittica e quello equatoriale è stato fissato una volta e per sempre proprio al momento della costruzione di questo strumento. Se in esso c'era un difetto, questo influenzerà le coordinate di ciascuna stella misurata con l'aiuto di questa sfera armillare. L'errore nel valore stimato dell'angolo φ è di natura completamente diversa. È singolo per ogni stella e cambia quando l'osservatore misura le coordinate di più stelle consecutive.
Bisogna quindi trovare la caratteristica degli errori di gruppo per le singole costellazioni dell'Almagesto e confrontarla con l'errore sistematico di ZodA, il gruppo di stelle dell'Almagesto misurato meglio.
3.2. Il calcolo degli errori sistematici per i singoli gruppi di costellazioni dell’Almagesto.
Il presente paragrafo analizza un totale di 21 piccoli gruppi di stelle dell'Almagesto. L'elenco è disponibile nella Tabella 6.5, la cui struttura è completamente identica a quella della Tabella 6.1. La nostra unica indicazione aggiuntiva riguarda il principio di selezione limitata delle configurazioni stellari. Tutte quelle menzionate in precedenza sono le costellazioni zodiacali prese dall'Almagesto, come pure le aree circostanti formate dalle stelle con nome ad eccezione di Canopo, Previndemiatrix e Procione, a causa della scarsità di stelle nel loro ambiente.
La posizione degli errori di gruppo per le singole costellazioni dell'Almagesto è associata ai seguenti problemi. Consideriamo un certo gruppo stellare G e troviamo i valori corrispondenti di
γGstat e φGstat. applicando il metodo dei minimi quadrati. Questo definirà anche la possibile minima discrepanza media quadratica residuale di σGmin, nonché la quota di stelle la cui discrepanza latitudinale residuale sia inferiore a 10'. Questa definirà anche il valore PGmin. in relazione al momento temporale t = 18. Tuttavia, a causa delle dimensioni ridotte di alcuni gruppi di stelle, la discrepanza statistica delle stime γGstat e φGstat. è troppo grande per servire da base per dei corollari giustificati.
Tabella 6.5. Il complesso stellare dei 21 gruppi di stelle dell'Almagesto; per ciascuno di questi gruppi sono stati calcolati i valori degli errori sistematici. Questi gruppi includono tutte le costellazioni zodiacali dell'Almagesto, così come i dintorni delle 12 stelle con nome, ad eccezione di Canopo e Previndemiatrix. La tabella contiene la numerazione di Bailey, ovvero i numeri delle stelle come indicati nel catalogo dell'Almagesto. |
||
Gruppo stellare dell’Almagesto |
Numero stellare di Bailey per gruppo |
Numero di stelle in un gruppo |
1. Costellazioni Zodiacali |
||
Ariete |
362-371, 373, 374, |
12 |
Toro |
380-388, 390, 391, 393-410 |
29 |
Gemelli |
424-440 |
17 |
Cancro |
449-454 |
6 |
Leone |
462-481, 483-488 |
26 |
Vergine |
497-516, 518-520 |
23 |
Bilancia |
529-534 |
6 |
Scorpione |
546-565 |
20 |
Sagittario |
570-573, 575-583, 585, 586, 590, 591, 593, 594, 596-598 |
22 |
Capricorno |
601-608, 610-627 |
26 |
Acquario |
629-650, 652-656, 658-660, 662-668 |
37 |
Pesci |
674-695, 697, 699-701, 704-706 |
29 |
2. Dintorni e Stelle dell’Almagesto con Nome |
||
Antares |
546-569 |
24 |
Aselli |
449-454, 456-461 |
12 |
Capella |
220-233 |
14 |
Aquila |
286-300 |
15 |
Vega = Lira |
149-158 |
10 |
Arturo |
88-96, 98, 100-110 |
21 |
Sirio |
812, 818-835, 837-846 |
29 |
Spiga |
497-503, 505-515, 518-526 |
27 |
Regolo |
462-481, 483-488, 491-493 |
29 |
Tuttavia, il valore di σGmin definisce il limite più basso dei possibili errori medi quadratici per il gruppo G. Questo valore minimo dei possibili errori risulta ruotando il sistema delle coordinate per mezzo degli angoli γGstat e φGstat. Ovviamente, i valori di γGstat e φGstat possono differire notevolmente da quelli di γstat e φstat che sono stati calcolati per il numero maggiore delle stelle incluse nel gruppo G.
Il criterio di identità dell'errore di gruppo per il gruppo G e l'errore sistematico calcolato per un numero elevato di stelle, potrebbero essere espressi con l'equazione approssimativa σGmin ≈ σG1 dove σGmin è la discrepanza media quadratica residuale per il gruppo G, dopo che il sistema delle coordinate è ruotato per gli angoli γstat e φstat. Infatti, la menzionata equazione approssimativa sta a significare che γGstat e φGstat sono dei valori “quasi” ottimali. Per poter supportare questo criterio, definiamo i valori ausiliari di PGmin e PG1 che rappresentano la quota di stelle del gruppo G la cui discrepanza latitudinale non supera i 10' dopo le rispettive rotazioni di (γGstat e φGstat) e (γstat e φstat). Dobbiamo anche tener conto del caso di PGmin ≈ PG1 e possiamo concludere che il gruppo G possiede di fatto lo stesso valore dell'errore sistematico delle stelle di un gruppo più numeroso. Dobbiamo far notare che l'ultima proporzione approssimativa non è implicita alla prima, ma capita che dimostra la nostra affermazione in modo indipendente. Qualora volessimo ignorare il moto proprio delle stelle, dovremmo anche sottolineare che entrambe le proporzioni sono temporalmente indipendenti. Pertanto, la loro verifica pratica può essere condotta per un solo momento nel tempo, vale a dire per uno qualsiasi di questi momenti.
Tabella 6.6. I risultati dei calcoli per i 21 gruppi di stelle dell'Almagesto. Qui, corrispondono alla discrepanza latitudinale media quadratica nel gruppo G, quella iniziale e quella residuale, come anche quella che scaturisce dalla compensazione dell'errore sistematico in G come stimato per ZodA. Riportiamo anche i valori percentuali stellari di PGinit, PGmin e PG1 con una discrepanza latitudinale minima di 10'. |
|||||||
| Gruppo stellare | Indicazioni di G | σGinit | σGmin | σG1 | PGinit | PGmin | PGmin |
1. Costellazioni Zodiacali |
|||||||
Ariete |
ZI |
19.7 |
17.2 |
18.9 |
45.5 |
45.5 |
72.7 |
Toro |
Z2 |
23.2 |
18.1 |
20.6 |
27.6 |
41.4 |
41.4 |
Gemelli |
Z3 |
17.8 |
10.5 |
11.0 |
29.4 |
82.4 |
58.8 |
Cancro |
Z4 |
13.8 |
4.3 |
5.2 |
33.3 |
100.0 |
100.0 |
Leone |
Z5 |
20.2 |
11.1 |
11.2 |
19.2 |
65.4 |
65.4 |
Vergine |
Z6 |
18.4 |
13.6 |
14.4 |
39.1 |
56.5 |
47.8 |
Bilancia |
Z7 |
8.4 |
6.1 |
9.3 |
83.3 |
83.3 |
83.3 |
Scorpione |
Z8 |
18.8 |
13.7 |
15.1 |
30.0 |
65.0 |
55.0 |
Sagittario |
Z9 |
16.4 |
14.3 |
15.8 |
30.4 |
60.9 |
60.9 |
Capricorno |
Z10 |
16.2 |
10.6 |
11.3 |
42.3 |
65.4 |
57.7 |
Acquario |
Z11 |
28.6 |
17.3 |
19.2 |
18.4 |
44.7 |
44.7 |
Pesci |
Z12 |
22.5 |
21.5 |
21.7 |
51.7 |
41.4 |
34.5 |
2. Dintorni e Stelle dell’Almagesto con Nome |
|||||||
Antares |
S1 |
17.7 |
12.6 |
13.8 |
33.3 |
70.8 |
58.3 |
Aselli |
S2 |
15.7 |
11.0 |
12.1 |
33.3 |
58.3 |
66.7 |
Capella |
S3 |
34.6 |
30.3 |
34.0 |
35.7 |
14.3 |
64.3 |
Aquila |
S4 |
24.0 |
23.7 |
26.7 |
40.0 |
33.3 |
13.3 |
Vega = Lira |
S5 |
20.0 |
14.1 |
17.1 |
50.0 |
60.0 |
30.0 |
Arturo |
S6 |
24.2 |
17.2 |
20.0 |
19.0 |
38.1 |
28.5 |
Sirio |
S7 |
15.2 |
11.9 |
25.9 |
47.4 |
52.6 |
15.8 |
Spiga |
S8 |
17.9 |
14.1 |
14.5 |
44.4 |
48.1 |
48.1 |
Regolo |
S9 |
25.2 |
21.0 |
21.1 |
17.2 |
58.6 |
58.6 |
Abbiamo calcolato i valori di σG1 e PG1 per i diversi gruppi G dell'Almagesto e il momento temporale t =18. Ribadiamo che questi valori sono uguali alla rispettiva discrepanza latitudinale media quadratica e alla quota di stelle il cui valore di discrepanza latitudinale non supera i 10', dato che il polo dell'eclittica coincide con il polo definito per il gruppo di stelle misurato più accuratamente nell'area ZodA. In altre parole, la condizione è che gli errori di gruppo devono essere pari ai valori di γzodAstat e φzodAstat.
La discrepanza latitudinale media quadratica e la percentuale delle stelle il cui valore di discrepanza latitudinale non supera i 10' (nel gruppo G senza la compensazione dell'errore sistematico), sono stati trascritti rispettivamente per t = 18 con σGinit e PGinit.
Se il valore di σG1 superasse solo leggermente il valore minimo possibile di σGmin, avremmo il diritto di supporre che il valore dell'errore di gruppo del gruppo stellare G sia uguale al valore dell'errore sistematico della regione celeste ZodA. La differenza tra i valori di PG1 e PGmin è tuttavia un altro criterio di prossimità per l'errore di gruppo e l'errore sistematico. Ricordiamo ai lettori che i valori σGmin e σG1 sono temporalmente indipendenti per le stelle immobili e solo marginalmente dipendenti dal tempo nel caso delle loro controparti mobili. Un'affermazione simile sarà vera per le stelle che finiscono nell'intervallo di 10' della discrepanza latitudinale.
La Tabella 6.6 contiene i dati numerici che abbiamo calcolato. La sua rappresentazione visiva la potete trovare nelle Figure 6.11 e 6.12. La Figura 6.11 contiene le informazioni sui valori di σGmin e σG1, come anche PGmin e PG1, per tutte le costellazioni zodiacali dell'Almagesto (indicate con Z1,…, Z12). La Figura 6.12 contiene i rispettivi risultati per i dintorni delle stelle con nome dell'Almagesto; sono stati contrassegnati con S1, ..., S9. Occorre dire che le aree circostanti le stelle zodiacali con nome nell'Almagesto non corrispondono pienamente alla rispettiva costellazione dello zodiaco. Questi aree sono costituite da quel gruppo di stelle della costellazione che ha ricevuto un nome nel sistema di Bayer. Queste stelle sono in genere le più luminose e quelle meglio identificabili dell'Almagesto, formando così una base solida per il corollario.
3.3. Gli errori di gruppo per le singole costellazioni della regione celeste dell’Almagesto misurata bene, sono praticamente identici all’errore sistematico scoperto come una caratteristica generale di questa zona.
L’implicazione chiave dei grafici riportati e della Tabella 6.6 è che le costellazioni zodiacali della regione celeste ZodA (ovvero Gemelli, Cancro, Leone, Vergine, Bilancia e Scorpione) nell’Almagesto possiedono le seguenti qualità considerevoli. L’errore medio quadratico σ1 e la percentuale delle stelle con la discrepanza latitudinale massima di 10’ calcolata in base all’assunto che l’errore di gruppo sia uguale a (γzodAstat e φzodAstat.) sono solo leggermente diversi dai valori di σmin e Pmin calcolati per la posizione ottimale del polo dell’eclittica nella costellazione presa in esame. La maggiore discrepanza tra i due valori è stata rilevata nella costellazione “più ordinata” della Bilancia, dove nessun valore di σinit, σmin o σ1 supera i 10’ e Pinit = Pmin = P1 = 83,3%. Questa è la percentuale di stelle il cui valore della discrepanza latitudinale è inferiore a 10’. L’equazione Pinit = Pmin = P1 è facile da spiegare: la costellazione in questione si trova praticamente sull’asse equinoziale, quindi non rimane affatto influenzata dalla rotazione.
Tuttavia, questo corollario può anche essere vero per le costellazioni della regione celeste ZodB, sebbene occorra tener conto di maggiori dettagli. Comunque sia, per il momento la veridicità o meno di questo corollario non ha alcuna importanza per noi, poiché la regione celeste ZodB dell'Almagesto non contiene stelle con nome.
Ciò nonostante, dobbiamo segnalare un singolo fatto curioso che è stato scoperto in relazione alla costellazione dell'Ariete. Anche se il valore di σ1 sia diventato più basso rispetto a σinit dopo la compensazione dell'errore sistematico scoperto in precedenza (si deve anchesi notare che la differenza tra σmin e σinit è piuttosto piccola, in altre parole P1 >> Pinit = Pmin), lo spostamento del polo dell'eclittica nella posizione calcolata per ZodA ha permesso di aumentare al 72.7 % la quota delle stelle dell'Almagesto misurate bene nella costellazione dell'Ariete.
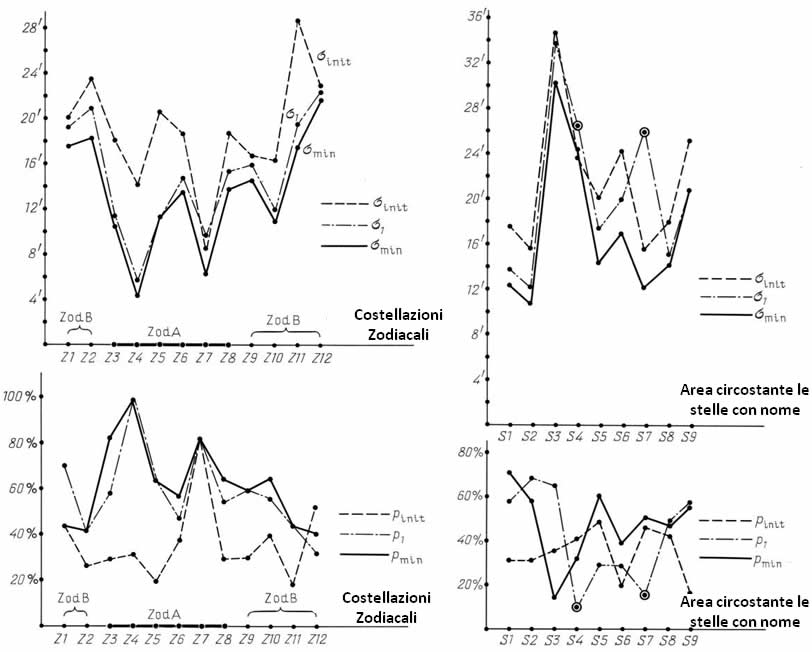
Le dipendenze di σmin, σ1, σinit, Pmin, P1, Pmin per le costellazioni zodiacali.
Le dipendenze di σmin, σ1, σinit, Pmin, P1, Pmin per le aree circostanti le stelle con nome.
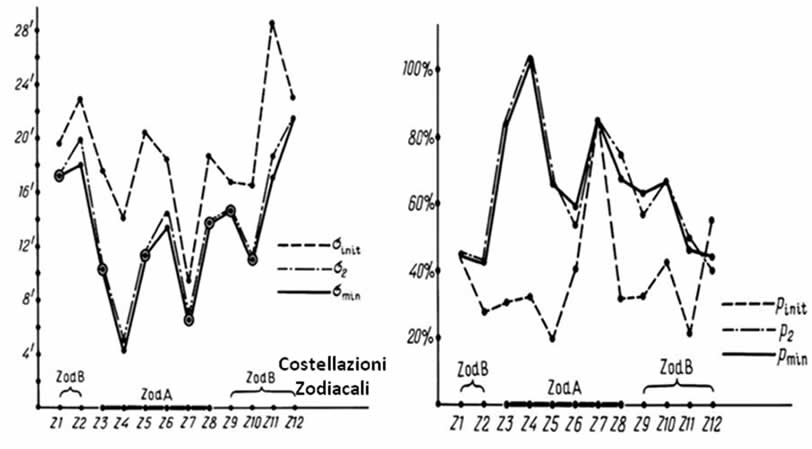
Figura 6.13.
Le dipendenze di σmin, σ2, σinit, Pmin, P2, Pmin per le costellazioni zodiacali.
La conclusione generale derivante dalla considerazione di tutte le costellazioni zodiacali è la seguente. Se la proporzione σmin << σinit fosse vera per il valore ottimale di σmin, la congettura che l'errore di gruppo sia uguale all'errore sistematico per la regione celeste ZodA e la conseguente compensazione di questo errore ci porterebbero alla proporzione di σ1 << σinit; le altre proporzioni valide includono P1 >> Pinit e Pmin >> Pinit. Questo è vero per le seguenti costellazioni dell'Almagesto: Gemelli, Cancro, Leone, Vergine, Scorpione, Capricorno e Acquario.
Se il valore di σmin fosse vicino a σinit, come regola σmin ≤ σ1 ≤ σinit, l'effetto di posizionare il polo eclittico nella posizione che corrisponde all'area ZodA non riuscirebbe a manifestarsi. Questo è vero per la costellazione dell'Ariete (come abbiamo sottolineato, la percentuale delle stelle misurate bene è cresciuta drammaticamente nel caso dell'Ariete), come anche per il Toro, Bilancia, Sagittario e Pesci.
Al di fuori delle costellazioni indicate sopra, le ottime caratteristiche di precisione della Bilancia nell'area celeste ZodA rimangono praticamente invariate dopo lo spostamento del polo dell'eclittica dalla posizione ottimale alla posizione che corrisponde a ZodA. Dopo questa operazione le caratteristiche di precisione dell'Ariete diventano ancora migliori, mentre quelle di tutte le altre costellazioni rimangono nella media.
Un esempio tipico è il Toro, con σinit= 23.2', σmin= 18,1', σ1 = 20,6', Pinit= 27,6% e Pmin = P1 = 41,4%. La costellazione dei Pesci differisce da tutte le altre costellazioni dell'Almagesto, con Pmin < Pinit e P1 < Pinit, dato che σinit ≈ σmin ≈ σ1.
3.4. In che modo la compensazione dell'errore sistematico che abbiamo scoperto influenza le caratteristiche di precisione delle aree circostanti le stelle con nome.
La situazione delle aree circostanti le stelle con nome dell'Almagesto è più varia. Prima di tutto, parliamo delle aree circostanti dell'Aquila e di Sirio. In entrambi i casi, la compensazione dell'errore sistematico scoperto, una caratteristica della regione celeste ZodA, porta a quanto segue. Innanzitutto, osserviamo una crescita della discrepanza latitudinale media quadratica, che è piuttosto sostanziale nel caso di Sirio, da 15,2 'a 25,9'. In secondo luogo, la percentuale delle stelle misurate bene si riduce (dal 40% al 13,3% per l'Aquila e dal 47,4% al 15,8% per Sirio). La conclusione ovvia da fare è che l'errore di gruppo effettuato dal compilatore durante le misurazioni dei circondari dell'Aquila e di Sirio è sostanzialmente diverso dall'errore sistematico della regione celeste ZodA. Sfortunatamente, è impossibile calcolare questi errori in modo veritiero. Pertanto, Sirio e l'Aquila sono state escluse da ulteriori considerazioni.
Le aree circostanti le altre stelle con nome hanno sostanzialmente le stesse proprietà delle costellazioni zodiacali, vale a dire che le stelle nei dintorni di Antares, Aselli, Arturo, Spiga e Regolo riducono notevolmente l'errore medio quadratico, facendolo avvicinare ai valori minimi possibili dopo la compensazione dell'errore di gruppo, che per la regione ZodA equivale all'errore sistematico. La percentuale delle stelle il cui valore di discrepanza latitudinale è inferiore a 10' (P1) crescerà in modo drammatico rispetto al valore iniziale di Pinit. Le aree circostanti Capella hanno la stessa proprietà della costellazione dell'Ariete, vale a dire che la discrepanza latitudinale media quadratica di quest'area non cambia di molto dopo lo spostamento del polo dell'eclittica dalla posizione iniziale a quella ottimale e quindi anche nella posizione calcolata per la regione celeste ZodA. Tuttavia, in quest'ultima posizione la quota delle stelle che rientrano nel valore di discrepanza latitudinale di 10', è aumentato drasticamente nelle vicinanze di Capella, raggiungendo il 64,3%. Per fare un confronto, vi facciamo notare che nella posizione iniziale questa quota era pari al 35,7% e solo al 14,3% nella posizione ottimale dettata dalla discrepanza latitudinale media quadratica. Al contrario, le stelle confinanti con Vega hanno dimostrato una sostanziale riduzione della discrepanza latitudinale media quadratica. Tuttavia, quando abbiamo spostato il polo dell'eclittica nella posizione caratteristica per la regione celeste ZodA, si è ridotto il numero di stelle con un valore di discrepanza latitudinale di 10' e anche meno. Pertanto, la natura degli errori di gruppo nelle vicinanze di Vega e Capella rimane poco chiara. Non c'è da stupirsi, è opportuno tenere a mente che queste stelle sono abbastanza distanti dalla regione celeste ZodA.
3.5. La scoperta dell'unico errore sistematico realizzato dal compilatore dell’Almagesto per la regione ZodA e la maggior parte delle stelle con nome.
Anche se abbiamo scoperto una certa vicinanza tra le caratteristiche di σ1 e P1, rispettivamente per σmin e Pmin (che testimonia la natura sistematica di γstat), rimane aperta la questione se l'errore di φstat possa essere sistematico. La risolviamo nel modo seguente. Prendiamo in considerazione alcune costellazioni singole dell'Almagesto. Non andremo oltre le costellazioni zodiacali, ad ogni modo le sei stelle con nome che appartengono allo Zodiaco. Calcoliamo le caratteristiche di σ2 e P2 per queste costellazioni, che può essere fatto come segue. La prima caratteristica è la discrepanza media quadratica residuale, mentre la seconda è la quota di stelle in una costellazione la cui discrepanza latitudinale non superi i 10'. Entrambe le caratteristiche derivano dall'errore statistico
γstatZod A calcolato per la regione ZodA e da φ(2) calcolato come prerequisito necessario per la minimizzazione dell'errore σ2. In altre parole, questo è ciò a cui siamo giunti con la costellazione G:
σ2G = σ2G(t) = minφ σG(γstatZod A, φ, t), φ(2) = arg minφ σG(γstatZod A, φ, t).
Compiliamo la Tabella 6.7, che è simile alla Tabella 6.6. Inoltre, alcuni dati si ripetono per una migliore dimostrabilità. Nella Tabella 6.7 i valori di σ1 e P1 sono sostituiti da quelli di σ2 e P2. Disegniamo questi dati nella Figura. 6.13, che è simile alla Figura 6.11. Sia la tabella che il grafico rendono evidente che la compensazione dell'errore sistematico γstatZod A nelle costellazioni zodiacali dell'area celeste ZodA e la variazione del valore φ possono darci i valori minimi possibili di σ2, che sono molto vicini o addirittura uguali a σmin. Allo stesso modo, il valore di P2 sarà vicino o uguale a Pmin. Abbastanza sorprendentemente, lo stesso vale per le costellazioni della regione celeste ZodB.
Tutto quanto sopra dimostra oltre ogni dubbio che il valore di γstatZod A che abbiamo scoperto è di fatto l'errore sistematico commesso dal compilatore del catalogo dell'Almagesto mentre misurava le stelle della regione celeste ZodA, così come le stelle con nome ad eccezione di Sirio, Aquila e Canopo. Il valore di γstatZod A può essere il risultato medio di molti singoli errori di misurazione e non vi è motivo di considerarlo un errore sistematico. Inoltre, il valore di φstat è stato calcolato piuttosto approssimativamente, il che lo rende piuttosto scarso di informazioni.
Tabella 6.7. I risultati dei calcoli per i 21 gruppi di stelle dell'Almagesto. Qui, σGinit, σGmin e σG2 corrispondono alla discrepanza latitudinale media quadratica nel gruppo G, quella iniziale e quella residuale, come anche quella che scaturisce dalla compensazione dell'errore sistematico in G come stimato per ZodA con la scelta ottimale del parametro φ. Riportiamo anche i valori percentuali stellari di PGinit, PGmin e PG2 con una discrepanza latitudinale minima di 10'. |
|||||||
Gruppo stellare |
Indicazioni di G |
σGinit | σGmin | σG2 | PGinit | PGmin | PG2 |
1. Costellazioni Zodiacali |
|||||||
Ariete |
ZI |
19.7 |
17.2 |
17.2 |
45.5 |
45.5 |
45.7 |
Toro |
Z2 |
23.2 |
18.1 |
20.2 |
27.6 |
41.4 |
41.4 |
Gemelli |
Z3 |
17.8 |
10.5 |
10.6 |
29.4 |
82.4 |
82.4 |
Cancro |
Z4 |
13.8 |
4.3 |
4.5 |
33.3 |
100.0 |
100.0 |
Leone |
Z5 |
20.2 |
11.1 |
11.1 |
19.2 |
65.4 |
65.4 |
Vergine |
Z6 |
18.4 |
13.6 |
14.4 |
39.1 |
56.5 |
52.2 |
Bilancia |
Z7 |
8.4 |
6.1 |
6.1 |
83.3 |
83.3 |
83.3 |
Scorpione |
Z8 |
18.8 |
13.7 |
13.7 |
30.0 |
65.0 |
70.0 |
Sagittario |
Z9 |
16.4 |
14.3 |
14.4 |
30.4 |
60.9 |
56.5 |
Capricorno |
Z10 |
16.2 |
10.6 |
10.6 |
42.3 |
65.4 |
65.4 |
Acquario |
Z11 |
28.6 |
17.3 |
18.7 |
18.4 |
44.7 |
47.4 |
Pesci |
Z12 |
22.5 |
21.5 |
21.7 |
51.7 |
41.4 |
37.9 |
4. Corollari.
Corollario 1. È stato dimostrato statisticamente che i poli dell'eclittica delle stelle nelle regioni celesti A e ZodA sono molto vicini tra loro, il che rende uguale il valore dell'errore sistematico commesso dal compilatore dell'Almagesto in queste parti del cielo.
Corollario 2. L'analisi statistica che abbiamo condotto non dà motivo di credere che i valori dell'errore sistematico nel catalogo dell'Almagesto per le regioni celesti C, D, M, B e ZodB, abbiano qualcosa in comune con i valori caratteristici delle aree A e ZodA. Gli errori sistematici delle aree C, D e M molto probabilmente differiscono dalle loro controparti nelle aree A e ZodA. Non possiamo dire nulla di concreto sugli errori che caratterizzano le regioni celesti B e ZodB, poiché il materiale numerico che abbiamo a nostra disposizione non ci consente di arrivare a una conclusione statistica inequivocabile.
Corollario 3. La precisione nelle misurazioni delle coordinate stellari sono molto più alte per A e ZodA che per qualsiasi altra regione celeste.
Corollario 4. Nell'Almagesto, la discrepanza latitudinale media quadratica residuale per la regione celeste ZodA è uguale 12.8'. Circa i 2/3 di tutte le stelle di questa parte del cielo hanno una discrepanza latitudinale inferiore a 10', per cui si adattano al margine di precisione dichiarato di 10' per il catalogo dell'Almagesto. I valori corrispondenti per la regione celeste A equivalgono a 16,5' e 1/2.
Corollario 5. Uno studio delle costellazioni zodiacali e delle aree circostanti le stelle con nome dell'Almagesto permette di concludere che il parametro γ, che indica l'errore nell'angolo dell'eclittica, è un errore sistematico. Per quanto riguarda il parametro φ, potrebbe anche essere il valore al quadrato degli errori di gruppo o individuali.
Corollario 6. L'errore di gruppo γ per le costellazioni dei Gemelli, Cancro, Leone, Vergine, Bilancia, Scorpione,Sagittario e Capricorno, nonché le aree circostanti Antares, Aselli, Arturo, Spiga e Regolo, è vicino all'errore sistematico , che è caratteristico di ZodA, la parte del cielo misurata meglio nell'Almagesto, e potrebbe persino coincidere con esso.
Corollario 7. Non si può dire nulla di definitivo sui valori degli errori di gruppo fatti dal compilatore dell'Almagesto nel caso dell'Ariete e del Toro. Possono sia coincidere con gli errori scoperti per ZodA o essere diversi dai loro valori. Non può essere calcolato nemmeno l'errore nelle zone circostanti le stelle Capella e Vega.
Corollario 8. Gli errori di gruppo nelle aree circostanti Sirio e l'Aquila differiscono dall'errore caratteristico per la regione celeste ZodA. Tuttavia, non siamo riusciti a calcolare i valori di questi errori. L'errore di gruppo fatto per la costellazione dei Pesci è molto probabile che sia diverso da .