CAPITOLO 7
La datazione del catalogo stellare dell’Almagesto. Il metodo statistico e quello geometrico.
1. Il kernel informativo del catalogo è formato dalle stelle con nome misurate bene.
L'analisi del catalogo stellare Almagesto descritta nei Capitoli 2-6 aveva l'obiettivo di ridurre le discrepanze latitudinali nelle coordinate stellari compensando l'errore sistematico scoperto nel catalogo.
Di conseguenza, abbiamo dimostrato che quando il compilatore dell'Almagesto afferma che il margine di precisione delle sue misurazioni inferiore a 10' è giustificato, almeno per quanto riguarda le latitudini della maggior parte delle stelle nella regione celeste A. Riteniamo che questa circostanza sia di fondamentale importanza.
Tuttavia, possiamo datare il catalogo dell'Almagesto considerando solo le stelle veloci e misurabili precisamente a priori. In altre parole, ai fini della datazione occorrono le stime individuali degli errori. Le nostre caratteristiche statistiche non possono dirci nulla sulla precisione delle misurazioni delle coordinate stellari effettive o sulle stelle misurate con la massima precisione.
La scelta delle stelle può essere definita solo da considerazioni ragionevoli basate sui metodi pratici di misurazione delle coordinate stellari utilizzati dagli antichi (vedere Capitolo 1). È risaputo che le misurazioni della maggior parte delle coordinate stellari si son sempre basate sulle cosiddette stelle di riferimento, il cui numero è piuttosto piccolo rispetto al numero totale delle stelle nel catalogo.
Cominciamo ribadendo una serie di considerazioni espresse nei capitoli precedenti, che serviranno da base per il nostro metodo di datazione.
Sfortunatamente, non sappiamo quale sia stato l'insieme delle stelle di riferimento usato dall'autore dell'Almagesto. Tutto ciò che sappiamo è che deve aver incluso Regolo e Spiga, dal momento che la misurazione delle loro coordinate è stata discussa in specifiche sezioni separate dell'Almagesto. Tuttavia, avrebbe senso presumere che il compilatore del catalogo fu più preciso quando misurò le coordinate delle stelle con nome. Come abbiamo detto in precedenza, nell'Almagesto ce ne sono dodici: Arturo, Regolo, Spiga, Previndemiatrix, Capella, Lira = Vega, Procione ,Sirio, Antares, Aquila = Altair, Aselli e Canopo.
L'identità delle stelle di riferimento di Tolomeo (quelle usate per le misurazioni delle coordinate planetarie) è un problema che fu studiato in [1120]. E' venuto fuori che le stelle in questione furono le seguenti (Tolomeo in realtà le menziona come stelle di riferimento dell'eclittica): Aldebaran = α Tau, Regolo, Spiga e Antares. Nell'Almagesto, tre di loro hanno un nome proprio, vale a dire Regolo, Spiga e Antares. A quanto pare, per le osservazioni planetarie Tolomeo dovette aggiungere anche Aldebaran. Tra l'altro, tutte e quattro le stelle sono state incluse nella nostra Tabella 4.3.
Le dodici stelle con nome dell'Almagesto sono luminose e chiaramente visibili sullo sfondo, e offrono un utile insieme di punti di riferimento sulla sfera celeste. La circostanza più importante è che una parte sufficientemente grande di queste stelle è caratterizzata da una velocità sostanziale di moto proprio, in particolare Arturo, Procione e Sirio.
Delle dodici stelle dell'Almagesto, sette si trovano nell'area celeste Zod A o nelle sue immediate vicinanze. Sono le seguenti: Arturo, Spiga, Procione, Aselli, Previndemiatrix, Regolo e Antares. Nove delle stelle con nome circondano l'area A: la precedente serie deve essere integrata da Lira = Vega e Capella. Per cui, anche se queste 12 stelle non fossero state usate come riferimento, molto probabilmente le loro coordinate sarebbero state misurate con sufficiente precisione.
Tuttavia, nonostante la probabile alta precisione delle loro coordinate misurate nell'Almagesto, le stelle comprese in questo gruppo non sono affatto di uguale importanza. La nostra analisi ha rivelato quanto segue:
- Canopo si trova nel lontano sud, quindi la precisione delle misurazioni è fortemente influenzata dalla rifrazione. Pertanto, nonostante tutti gli sforzi del compilatore dell'Almagesto, le coordinate di questa stella indicate nel catalogo sono note a priori per essere sbagliate per più di un grado.
- Le coordinate di Previndemiatrix misurate dal compilatore dell'Almagesto rimangono a noi sconosciute: conosciamo solo i risultati delle ultime ricerche ([1339]).
- Come abbiamo scoperto nel Capitolo 6, gli errori di gruppo nelle aree circostanti Sirio e l'Aquila non concordano con l'errore inerente alle coordinate di tutte le altre stelle. Non siamo in grado di calcolare la percentuale di questi errori: di conseguenza nel loro caso la compensazione non servirà a nulla.
Quindi, siamo giunti alle 8 stelle con nome che possiamo utilizzare ai fini della datazione. Le stelle che le circondano hanno un singolo errore di gruppo nelle loro coordinate; per lo meno, il componente γ di questo errore è lo stesso in tutti i casi. Chiameremo queste stelle come il kernel informativo del catalogo dell'Almagesto.
Avrebbe senso formulare la seguente ipotesi. Se il tasso di precisione dichiarato dal compilatore del catalogo fosse effettivamente vero, la sua manifestazione nel kernel informativo del catalogo sarebbe garantita dopo la compensazione dell'errore di gruppo.
Si tratta proprio dell'ipotesi su cui si basa la datazione dei cataloghi stellari.
Tuttavia, il fatto che il kernel informativo del catalogo abbia la capacità di aiutarci con la sua datazione, è tutt'altro che ovvio. In linea generale, il fatto che siamo riusciti a ricostruire i valori effettivi degli errori casuali inerenti al catalogo dell'Almagesto per mezzo della compensazione dell'errore di gruppo, non implica che i singoli errori nelle coordinate del kernel del catalogo stellare siano uguali. Non è molto probabile che esista una discrepanza di questo tipo: che la stella centrale di un gruppo sembra avere lo stesso tipo di errore sia nelle sue coordinate che nelle aree circostanti più vicine. Tuttavia, a rigor di termini, l'ipotetica esistenza di una tale discrepanza deve essere comunque presa in considerazione. A parte questo, non si deve escludere la possibilità che le coordinate di una stella inclusa nel kernel informativo del catalogo, siano state misurate con un margine di errore superiore a 10'.
Quanto sopra ci dice che se riuscissimo a trovare un momento nel tempo conforme ai requisiti della nostra ipotesi, saremmo in grado di dimostrare ancora una volta la correttezza delle nostre congetture statistiche iniziali.
2. Le considerazioni preliminari in riferimento alla datazione del catalogo dell’Almagesto tramite le variazioni nelle coordinate delle stelle con nome.
Nel primo paragrafo abbiamo individuato il gruppo delle stelle che abbiamo chiamato il kernel informativo dell'Almagesto. Di seguito considereremo il suo comportamento nei dettagli. Ciò che dobbiamo analizzare qui è il comportamento di tutte le 12 stelle con nome dell'Almagesto in una sola volta. Questo studio preliminare dimostra perfettamente bene di quanto aumenti il tasso di precisione del catalogo dell'Almagesto dopo la compensazione dell'errore sistematico. Inoltre, fornisce ulteriori spiegazioni sul fatto che tre stelle con nome su dodici (Canopo, Sirio e Aquila = Altair) rompono l'omogeneità di tutto il campione. Abbiamo appreso che queste stelle sono dei “refusi” rispetto a tutte le altre stelle con nome. Di seguito, nel nostro studio di tutte e 12 le stelle con nome, useremo le coordinate di Previndemiatrix da [1339] che a quanto pare furono calcolate da Halley. Useremo ΔBi(t, γ, φ) per riferirci alla differenza tra la latitudine della stella i e il kernel informativo dell'Almagesto dopo la compensazione dell'errore sistematico (γ, φ) e la latitudine effettiva calcolata per l'epoca t.
Tabella 7.1. Le discrepanze latitudinali delle 12 stelle con nome dell'Almagesto e la loro dipendenza dalla presunta datazione. L'errore sistematico rilevato nel catalogo dell'Almagesto qui non è stato compensato. |
||||||
Il nome della stella e il |
Anni | |||||
| 1800 d.C. | 1400 d.C. | 900 d.C. | 400 d.C. | 100 d.C. | 200 a.C. | |
Arturo (110) |
37.8 | 21.2 | 0.9 | 19.3 | 31.4 | 43.3 |
Sirio (818) |
23.6 | 18.3 | 11.7 | 5.1 | 1.2 | 2.6 |
Aquila = Altair (288) |
8.6 | 9.4 | 10.5 | 11.8 | 12.6 | 13.4 |
Previndemiatrix (509) |
13 | 14.3 | 15.8 | 17.1 | 17.8 | 18.4 |
Antares (553) |
32.6 | 29.5 | 25.5 | 21.6 | 19.3 | 17 |
Aselli (452) |
30.5 | 28.5 | 25.9 | 23.2 | 21.5 | 19.8 |
Procione (848) |
11.2 | 16 | 21.9 | 27.6 | 31.1 | 34.4 |
Regolo (469) |
17.5 | 16.6 | 15.4 | 14 | 13 | 12.1 |
Spiga (510) |
2.4 | 0.7 | 1.3 | 3.1 | 4.2 | 5.2 |
Lira = Vega (149) |
15.4 | 14.2 | 12.5 | 10.8 | 9.8 | 8.7 |
Capella (222) |
21.9 | 21.7 | 21.3 | 21 | 20.8 | 20.6 |
Canopo (892) |
51 | 54.2 | 58.2 | 62.3 | 64.8 | 67.3 |
Prima Considerazione. Osserviamo la correlazione tra la precisione delle coordinate latitudinali delle stelle con nome dell'Almagesto e il valore del grado del catalogo che equivale a 10', supponendo che quest'ultimo non contenda degli errori sistematici globali. La Tabella 7.1 contiene i valori della discrepanza latitudinale assoluta di tutte e 12 le stelle con nome dell'Almagesto che dipendono dalla presunta datazione t. Nella prima colonna possiamo vedere il numero dato alle stelle dell'Almagesto (la numerazione di Bailey). I valori delle discrepanze latitudinali sono stati riportati in gradi d'arco.
La Tabella 7.1 dimostra che per 7 delle 12 stelle con nome dell'Almagesto la discrepanza latitudinale supera il limite di 10'. Le colonne che corrispondono al 100 d.C., che è la datazione di Scaligero dell'Almagesto (l'epoca di Tolomeo) e al 200 a.C. (l'epoca di Ipparco) attirano principalmente la nostra attenzione a causa del vergognoso errore nelle coordinate di Arturo, circa 30' o 40'. È peculiare che la stella dell'Emisfero Boreale più luminosa e più visibile, sia stata osservata da Tolomeo e da Ipparco di gran lunga peggio di tutte le altre stelle. Inoltre, il testo dell'Almagesto implica che le coordinate di Regolo sono state misurate più volte durante la compilazione del catalogo e che la stella in questione è nota per essere stata uno dei punti di riferimento per la misurazione di tutte le altre stelle. Sarebbe ovvio aspettarsi che Tolomeo sia stato eccezionalmente attento nella misurazione di questa stella; pertanto, la discrepanza latitudinale deve essere inferiore a 10'. Facciamo notare che un'altra stella luminosa sull'eclittica, vale a dire Spiga, le cui coordinate furono misurate da Tolomeo durante la fase iniziale per poterla utilizzare come riferimento in un secondo momento (cfr. il Capitolo VII.2 dell'Almagesto, o [1358]), ha una discrepanza latitudinale di 5', meno della metà del valore di misura del catalogo.
Ora consideriamo l'errore sistematico che abbiamo scoperto nell'Almagesto (vedere il Capitolo 6). Siccome il complesso γ di questo errore varia solo leggermente rispetto all'intervallo tra l'inizio della nuova era e il Medioevo, come pure le variazioni del valore di φ influenzano difficilmente la scena, useremo i valori γ0 =21', φ0 = 0. Il valore γ0 = 21' è il valore medio di γ(t) per t dall'intervallo noto a priori.
Tabella 7.2. Le discrepanze latitudinali delle 12 stelle con nome dell'Almagesto e la loro dipendenza dalla presunta datazione dopo la compensazione dell'errore sistematico nelle coordinate stellari dell'Almagesto specificate dai parametri γ0 = 21' e φ0 = 0. |
||||||
Il nome della stella e il |
Anni | |||||
| 1800 d.C. | 1400 d.C. | 900 d.C. | 400 d.C. | 100 d.C. | 200 a.C. | |
Arturo (110) |
29.9 | 15.5 | 2.3 | 20 | 30.5 | 41 |
Sirio (818) |
44.2 | 39.2 | 32.7 | 25.9 | 21.8 | 17.5 |
Aquila = Altair (288) |
27 | 28.7 | 30.7 | 32.5 | 33.5 | 34.4 |
Previndemiatrix (509) |
15.6 | 14.9 | 13.8 | 12.6 | 11.8 | 11 |
Antares (553) |
13.3 | 11 | 8.5 | 6.2 | 4.9 | 3.7 |
Aselli (452) |
13.2 | 10.2 | 6.5 | 2.9 | 0.9 | 1.1 |
Procione (848) |
8.1 | 4 | 1.2 | 6.7 | 10.1 | 13.5 |
Regolo (469) |
6.1 | 3.5 | 0.4 | 2.7 | 5.1 | 6.2 |
Spiga (510) |
5.1 | 4.9 | 4.4 | 3.7 | 3.3 | 2.7 |
Lira = Vega (149) |
5.1 | 6.7 | 8.5 | 10 | 10.8 | 11.5 |
Capella (222) |
1.3 | 1.5 | 2.1 | 2.9 | 3.5 | 4.2 |
Canopo (892) |
71.5 | 75 | 79.2 | 83.1 | 85.4 | 87.6 |
Procediamo con la costruzione della Tabella 7.2, che è simile alla 7.1; l'unica differenza è che l'errore sistematico definito dai parametri γ0 = 21' e φ0 = 0 in tutte le coordinate stellari, ora viene preso in considerazione e compensato nel calcolo delle discrepanze latitudinali.
Il confronto delle due tabelle dimostra che dopo la compensazione dell'errore sistematico, le caratteristiche di precisione delle coordinate delle stelle con nome dell'Almagesto sono migliorate drasticamente per tutte le datazioni possibili. Le latitudini di Regolo e Spiga sono state misurate con un tasso di precisione che si aggira intorno ai 5' per ogni presunta datazione tra l'inizio della nuova era e la fine del Medioevo. Questo si correla bene con il fatto che queste due stelle godono della massima attenzione nel testo dell'Almagesto, vedere il libro stesso, Capitolo VII.2 ([1358]). Inoltre, se volessimo posizionare la datazione sull'intervallo di 6 ≤ t ≤ 10, ovvero il 900-1300 d.C., la discrepanza latitudinale non supererebbe i 10' (il valore di misura del catalogo) per 8 stelle con nome su 12, quelle situate nella regione celeste A che abbiamo scoperto nel Capitolo 6 mentre stavamo analizzando l'intero aggregato stellare del catalogo dell'Almagesto.
Va da sé che le considerazioni di cui sopra devono essere più esplicite. In particolare, dobbiamo studiare gli altri valori dei parametri γ e φ. Il presente capitolo contiene calcoli dettagliati e ulteriori dichiarazioni esplicite.
Seconda Considerazione. La seguente linea di argomentazione potrebbe fornire ulteriori informazioni pertinenti alla datazione del catalogo dell'Almagesto. Prendiamo in considerazione le discrepanze latitudinali ΔBi(t, γ, φ) di un certo insieme di stelle dell'Almagesto E, 1 ≤ i ≤ n per ogni momento t e tutti i valori di γ e φ. Li useremo per costruire dei grafici empirici di funzione relativi alla distribuzione dell'errore latitudinale per l'insieme di stelle E: Ft, γ, φ (x) =(1 / n) # {i: | ΔBi(t, γ, φ) | ≤ x}, dove n rappresenta la quantità di stelle nell'insieme E. Il confronto di queste funzioni di distribuzione per i diversi valori dei parametri t, γ e φ, possono permetterci di provare a trovare la combinazione di questi valori che minimizzeranno stocasticamente gli errori latitudinali dell'insieme E. Il tasso di differenza dell'errore per i differenti valori di t, γ e φ sarà il valore medio della differenza. Ovviamente, non possiamo giungere a delle conclusioni quantitative dal momento che abbiamo a disposizione solo 12 osservazioni e quindi dobbiamo solo fare riferimento al quadro qualitativo come prima approssimazione.

Figura 7.1.
Le funzioni empiriche della distribuzione dell’errore nelle latitudini stellari.
Il tasso di differenza dell'errore in questione può essere rappresentato come l'area contenuta tra i grafici di distribuzione delle funzioni Ft1, γ1, φ1(x) e Ft2, γ2, φ2(x) disegnati in una sola bozza. Entrambe le aree contenute tra i grafici devono essere prese con un segno più o meno a seconda della funzione che troviamo a destra e a sinistra dell'area in questione (vedi la Figura. 7.1). La funzione di distribuzione Ft0, γ0, φ0(x) che è situata a sinistra di tutte le altre funzioni Ft, γ, φ, in media corrisponde a una percentuale di errore latitudinale minima per l'insieme E. Sarebbe naturale considerare la datazione t0 e il valore dell'errore sistematico (γ0, φ0) come delle approssimazioni alla data effettiva di osservazione e all'effettivo errore sistematico commesso dall'osservatore.
Illustriamo quanto sopra con l'esempio di un altro famoso catalogo stellare risalente alla seconda metà del XVI secolo e compilato da Tycho Brahe. Il kernel informativo che useremo è composto da 13 stelle con nome prese dal catalogo di Tycho Brahe. Abbiamo calcolato le funzioni empiriche di distribuzione Ft, γ, φ per γ = φ = 0 e tre valori diversi di t: t = 3 (1600 d.C.), t = 3,5 (1550 d.C.) e t = 4 (1500 d.C.). Il risultato è visibile nella Figura 7.2. Questa illustrazione dimostra abbastanza bene che senza considerare la possibilità di un errore sistematico inerente al catalogo di Tycho Brahe (γ = φ = 0), l'epoca t = 3.5 risulta essere la datazione ottimale del catalogo (il 1550 d.C. circa). Infatti, questa è proprio la datazione per cui gli errori nelle 13 stelle con nome del catalogo saranno minimi secondo quanto detto sopra. La data del 1550 d.C. è molto vicina all'epoca conosciuta di quando fu compilato il catalogo di Tycho Brahe, vale a dire la seconda metà del XVI secolo.
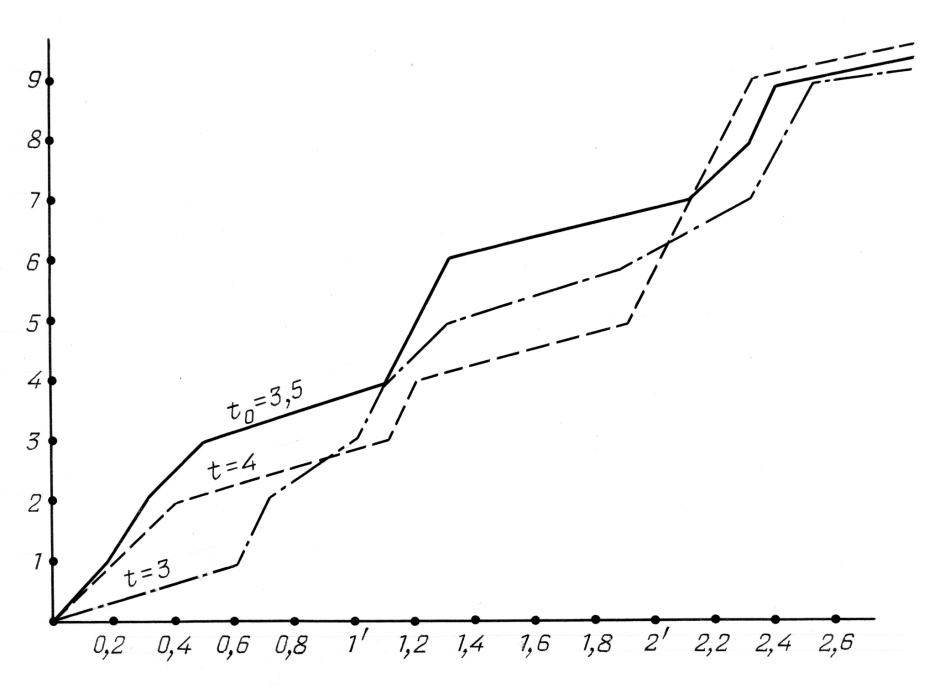
Figura 7.2.
Le funzioni empiriche di distribuzione per il catalogo
di Tycho Brahe;
il valore ottimale di t0 = 3.5.
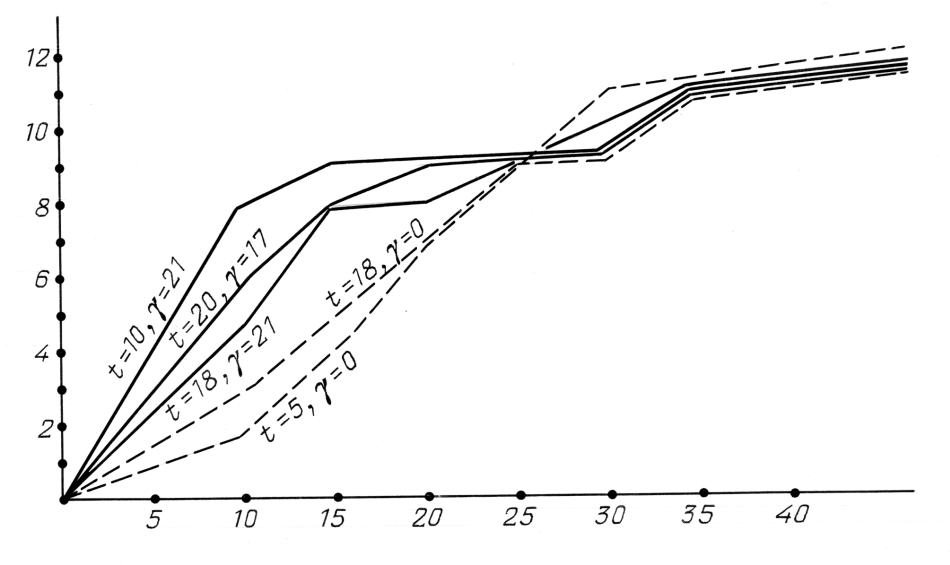
Figura 7.3.
Le funzioni empiriche di distribuzione Ft, γ, φ per le 12 stelle
con nome dell'Almagesto.
Il valore di φ è uguale a zero in tutti i casi.

Figura 7.4.
Le funzioni empiriche di distribuzione per le 13 stelle luminose
con nome dell'Almagesto con t = 1, 5, 10, 15 e 20.
Linee continue: γ = 21'; linee tratteggiate: γ = 0.
Forniamo l'elenco di queste 13 stelle del catalogo di Tycho Brahe. Innanzitutto, ci sono Regolo, Spiga, Arturo, Procione, Sirio, Lira = Vega, Capella, Aquila e Antares, che sono anche incluse nell'elenco delle stelle con nome dell'Almagesto. A parte queste, ci sono altre quattro stelle: Caph = β Cas, Denebola = β Leone, Polluce = β Gemma e Scheat = β Peg.
Ora prendiamo in considerazione le funzioni empiriche di distribuzione Ft, γ, φ per l'insieme di stelle E che è composto dalle 12 stelle con nome dell'Almagesto (vedi paragrafo 1). Nella Figura 7.3 si possono vedere i grafici di queste funzioni per t = 5 ossia il 1400 d.C., t = 10 ossia il 900 d.C., t = 18 ossia il 100 d.C. e t = 20 ossia il 100 a.C. con i valori variabili di γ. Il valore di φ è considerato ovunque pari a zero, dal momento che il quadro generale non viene quasi mai influenzato dalle variazioni di φ. I valori t = 10 ossia 900 a.C. e γ = 21' sono ottimali, vale a dire che generano gli errori meno gravi.
Le rappresentazioni grafiche risultanti per le funzioni Ft, t, γ, φ dell'Almagesto non sono molto sensibili ai cambiamenti nel contingente delle stelle con nome. Riportiamo le funzioni empiriche di distribuzione per tutte e 13 le stelle utilizzate nell'esempio di Tycho Brahe, questa volta dopo aver preso le coordinate dall'Almagesto, vedere la Figura 7.4. I valori di t = 10 e γ = 21' restano ottimali anche per questo elenco di stelle. Nella Figura 7.4 si può vedere chiaramente la differenza tra i valori di γ = 21' e γ = 0 già indicata sopra, vale a dire che tutti i grafici corrispondenti a γ = 21' in linea di massima si trovano a sinistra dei grafici creati per γ = 0, indicando che il tasso di errore più basso della precedente rispetto all'ultima. In altre parole, il valore di γ = 21' è “meglio” di γ = 0 per tutte le date t dell'intervallo scelto a priori.
Terza Considerazione. Concludiamo con la discussione del problema di quanto sia possibile espandere l'elenco delle stelle con nome dell'Almagesto usate come base per la datazione tramite i moti propri. Tuttavia, la precisione delle coordinate di questo elenco esteso (almeno per quanto riguarda le latitudini) non può assolutamente essere deteriorata. La prima impressione che si ottiene è che il modo più naturale per estendere l'elenco sarebbe quello di includere al suo interno tutte le stelle che ai nostri giorni hanno nome proprio (vedere la Tabella P1.2 in Appendice 1). La maggior parte delle stelle hanno ricevuto i nomi nel Medioevo, ma questa pratica continuò anche nel XVII-XIX secolo. È possibile che molte di loro fossero particolarmente significative per il compilatore del catalogo dell'Almagesto. Procediamo a selezionare solo quelle stelle della Tabella P1.2 (dall'Appendice 1) i cui nomi sono stati scritti in maiuscolo esattamente come in [1197]; si tratta delle stelle con nome più famose. Sono 37 di numero e sono state elencate nella Tabella 7.3.
Tuttavia, abbiamo scoperto che l'espansione del kernel informativo dell'Almagesto riduce drasticamente la precisione delle coordinate del campione e siamo particolarmente preoccupati che tutto questo influenzi le latitudini. Prendiamo in considerazione un “kernel espanso” che contenga le 37 stelle dell'Almagesto elencate nella Tabella 7.3. La Figura 7.5 mostra in che modo la discrepanza quadratica media si comporta per queste 37 stelle a seconda della datazione presunta dell'Almagesto. Dopo aver calcolato questa discrepanza, consentiamo che la variazione del tasso calcolato dell'errore sistematico possa fluttuare entro i ± 5' con il valore di 1 minuto per il parametro γ ed entro i 30' con il valore di 1 minuto per il parametro β. Il grafico risultante dimostra che anche se il minimo viene raggiunto intorno al 400 d.C., è molto poco chiaro. Il valore medio quadratico minimo equivale approssimativamente a 18 minuti. Se volessimo consentire una variazione di questo valore entro un intervallo di due minuti o un mero 10%, finiremmo con un intervallo di “datazione” di 1800 anni, non meno, tra il 600 a.C. e 1200 d.C. È perfettamente ovvio che questo risultato non ci è di alcun interesse; il motivo è che la precisione media dei calcoli di Tolomeo è troppo bassa per l'elenco delle 37 stelle in fase di studio ed è chiaramente insufficiente per la datazione del catalogo mediante i moti propri delle stelle.
Inoltre, questa immagine vaga è quella che otteniamo dalla nostra analisi delle latitudini, che come sappiamo sono più precise nel catalogo dell'Almagesto. Il quadro delle longitudini è ancora più vago.
Nelle Figure 7.6 e 7.7 si possono vedere i grafici delle dipendenze per la quantità di stelle nel kernel esteso il cui errore latitudinale calcolato non supera rispettivamente i 10 e 20 minuti rispettivamente e la presunta datazione dell'Almagesto. L'errore è stato calcolato dopo la compensazione dell'errore sistematico γ = 20'. Osserviamo le fluttuazioni all'interno di uno spazio più o meno costante di valori per tutto l'intervallo temporale in esame. Uno spazio latitudinale di 10 minuti copre da 3 a 13 stelle per diversi anni, anche se circa 11-16 stelle finiscono entro uno spazio di 20 minuti. Questi grafici non ci danno informazioni affidabili riguardo la datazione più probabile del catalogo.
Tabella 7.3. L'elenco delle stelle veloci che secondo BS4 possiedono dei vecchi nomi propri, tutte trascritte in lettere maiuscole come le stelle più famose del Medioevo. Qui ci sono tutte le aree celesti. L'elenco è preceduto dalle 8 stelle del kernel informativo dell'Almagesto, alcune delle quali non si collocano tra le stelle veloci. |
||||||
| Numero da BS4 e BS5 | Numero di Bailey | Magnitudine stellare secondo BS5 | vδ1900 [1197] | vδ1900 [1197] | Magnitudine stellare secondo l’Almagesto | Nome moderno della stella con il suo antico nome proprio come specificato in maiuscolo nel Catalogo delle Stelle Luminose [1197]. Indica che la stella in questione nel passato era molto conosciuta. |
| 5340 | 110 | -0.04 | -1.098 | -1.999 | 1 | 16α Boo (ARTURO) |
| 1708 | 222 | 0.08 | +0.080 | -0.423 | 1 | 13α Aur (CAPELLA) |
| 3982 | 469 | 1.35 | -0.249 | -0.003 | 1 | 32α Leo (REGOLO) |
| 2943 | 848 | 0.38 | -0.706 | -1.029 | 1 | 10α CMi (PROCIONE) |
| 5056 | 510 | 0.98 | -0.043 | -0.033 | 1 | 67α Vir (SPIGA) |
| 6134 | 553 | 0.96 | -0.007 | -0.023 | 2 | 21α Sco (ANTARES) |
| 7001 | 149 | 0.03 | +0.200 | +0.285 | 1 | 3α Lyr (LIRA = VEGA) |
| 3449 | 452 | 4.66 | -0.103 | -0.043 | 4-3 | 43γ Cnc (ASELLI) |
| 15 | 315 | 2.06 | +0.137 | -0.158 | 2-3 | 21α And (ALPHERATZ) |
| 21 | 189 | 2.27 | +0.526 | -0.177 | 3 | 11β Cas (CAPH) |
| 188 | 733 | 2.04 | +0.232 | +0.036 | 3 | 16β Cet (DENEB KAITOS = DIPHDA) |
| 337 | 346 | 2.06 | +0.179 | -0.109 | 3 | 43β And (MIRACH) |
| 617 | 375 | 2.00 | +0.190 | -0.144 | 3-2 | 13α Ari (HAMAL) |
| 1231 | 781 | 2.95 | +0.057 | -0.110 | 3 | 34γ Eri (ZAURAK) |
| 1457 | 393 | 0.85 | +0.065 | -0.189 | 1 | 87α Tau (ALDEBARAN) |
| 1791 | 400 | 1.65 | +0.025 | -0.175 | 3 | 112β Tau (ELNATH) |
| 2491 | 818 | -1.46 | -0.545 | -1.211 | 1 | 9α CMa (SIRIO) |
| 2890 | 424 | 1.58 | -0.170 | -0.102 | 2 | 66α Gem (CASTORE) |
| 2990 | 425 | 1.14 | -0.627 | -0.051 | 2 | 78β Gem (POLLUCE) |
| 4057 | 467 | 2.61 | +0.307 | -0.151 | 2 | 41γ Leo (ALGIEBA) |
| 4301 | 24 | 1.79 | -0.118 | -0.071 | 2 | 50α UMa (DUBHE) |
| 4534 | 488 | 2.14 | -0.497 | -0.119 | 1-2 | 94β Leo (DENEBOLA) |
| 4660 | 26 | 3.31 | +0.102 | +0.004 | 3 | 69δ UMa (NEGREZ) |
| 4905 | 33 | 1.77 | -0.109 | -0.010 | 2 | 77ε UMa (ALIOTH) |
| 4914 | 36 | 5.60 | -0.238 | +0.057 | 3 | 12α1 CVn (COR CAROLI) |
| 5054 | 34 | 2.27 | +0.119 | -0.025 | 2 | 79ζ UMa (MIZAR) |
| 5191 | 35 | 1.86 | -0.124 | -0.014 | 2 | 85η UMa (ALKAID) |
| 5267 | 970 | 0.61 | -0.020 | -0.023 | 2 | β Cen (AGENA) |
| 5793 | 111 | 2.23 | +0.120 | -0.091 | 2-1 | 5α CrB (ALPHECCA) |
| 5854 | 271 | 2.65 | +0.136 | +0.044 | 3 | 24α Ser (UNUKALHAI) |
| 6556 | 234 | 2.08 | +0.117 | -0.227 | 3-2 | 55α Oph (RAS ALHAGUE) |
| 6879 | 572 | 1.85 | -0.032 | -0.125 | 3 | 20ε Sgr (KAUS AUSTRALIS) |
| 7557 | 288 | 0.77 | +0.537 | +0.387 | 2-1 | 53α Aql (ALTAIR) |
| 7602 | 287 | 3.71 | +0.048 | -0.482 | 3 | 60β Aql (ALSHAIM) |
| 8162 | 78 | 2.44 | +0.150 | +0.052 | 3 | 5α Cep (ALDERAMIN) |
| 8728 | 1011 | 1.16 | +0.336 | -0.161 | 1 | 24α PsA (FOMALHAUT) |
| 8775 | 317 | 2.42 | +0.188 | +0.142 | 2-3 | 53β Peg (SCHEAT) |
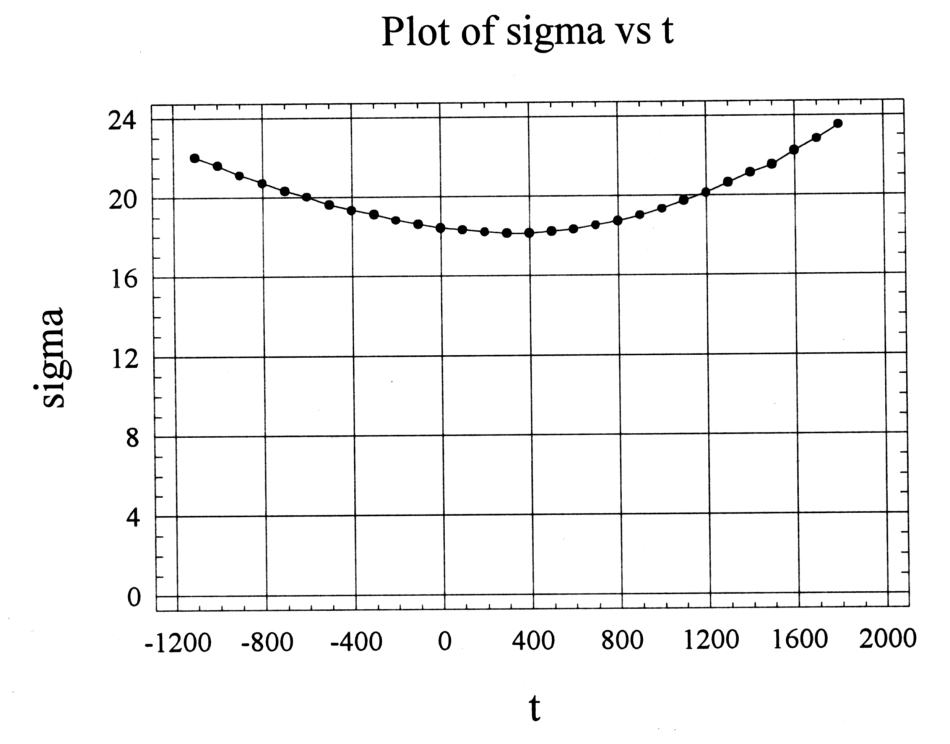
Figura 7.5.
La discrepanza media quadratica per le 37 stelle
dell'Almagesto elencate nella Tabella 7.3 come
una presunta funzione di datazione.
L'errore sistematico γ del catalogo dell'Almagesto è stato compensato
nel calcolo della discrepanza.
A parte questo, la discrepanza media
quadratica desiderata è stata ridotta al minimo in conformità
con le variazioni di γ = γstat ± 5 '; β = 0 ± 30 '.
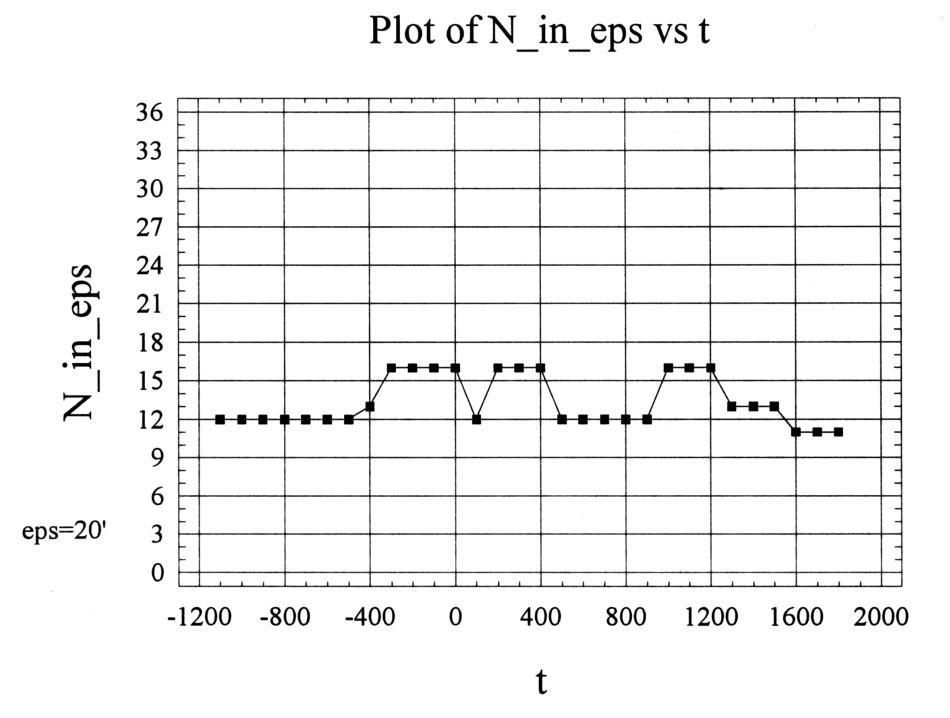
Figura 7.7.
Asse verticale: il numero delle stelle dell'Almagesto
dall'elenco delle 37 (vedere la Tabella 7.3)
la cui discrepanza latitudinale non supera i 20'.
Asse orizzontale: la presunta datazione del catalogo.

Figura 7.6.
Asse verticale: il numero delle stelle dell'Almagesto
dall'elenco delle 37 (vedere la Tabella 7.3)
la cui discrepanza latitudinale non supera i 10'.
Asse orizzontale: la presunta datazione del catalogo.

Figura 7.8.
La deviazione media quadratica delle 37 stelle dell'Almagesto
elencate nella Tabella 7.3, la cui discrepanza latitudinale non supera
i 30 minuti per la presunta datazione in questione.
Il grafico è stato costruito come la funzione della presunta
datazione dell'Almagesto.
L'errore sistematico γ del catalogo è stato compensato
durante la ricerca della discrepanza.
A parte questo, la discrepanza media quadratica è stata
minimizzata dalle variazioni di γ = γstat ± 5 '; β = 0 ± 30 '.
Nella Figura 7.8 riportiamo il grafico della discrepanza media quadratica della dipendenza simile al grafico della Figura 7.5. Tuttavia, le uniche stelle che abbiamo preso in considerazione questa volta sono state quelle che hanno una discrepanza latitudinale inferiore a 30 minuti per una determinata datazione. Si può vedere che il grafico è formato da segmenti di parabola leggermente inclinati, i cui minimi cadono in diversi anni sull'asse del tempo. Per cui, diverse parti dell'elenco delle 37 stelle contengono le vallate delle rispettive parabole sparse per tutto l'intervallo storico.
L'instabilità scoperta nelle vallate ci dice che questo metodo di datazione è molto impreciso a causa del fatto che le vallate di molte parabole si trovano a notevole distanza dalla data di compilazione del catalogo. Pertanto, la variazione del contingente stellare distribuirà caoticamente queste vallate per l'intera lunghezza dell'intervallo storico.
In linea generale, la manifestazione estremamente scarsa della vallata del grafico nella Figura 7.8 avviene nel periodo 700-1600 d.C., che non è di alcuna utilità per una datazione affidabile.
Abbiamo anche considerato altre possibilità di espansione per il kernel informativo dell'Almagesto, ad esempio usando come criterio la luminosità stellare. Hanno portato quasi tutti a una drastica riduzione della precisione delle coordinate stellari e ciò può essere di fatto considerato come l'eliminazione della dipendenza tra la datazione delle osservazioni e le caratteristiche dell'elenco esteso. Tuttavia, abbiamo scoperto che l'errore informativo consente di fatto la naturale espansione senza una drastica diminuzione della precisione. Questo problema sarà considerato nei dettagli di seguito.
<
3. La procedura della datazione statistica.
3.1. La descrizione della procedura di datazione.
L'ipotesi sulle stelle con nome dell'Almagesto misurate in corrispondenza del tasso di aberrazione di 10 minuti, ci consente di fornire una datazione effettiva piuttosto approssimativa dell'Almagesto nel paragrafo 2. Abbiamo dimostrato che la configurazione del kernel informativo del catalogo dell'Almagesto varia nel corso del tempo a una velocità sufficientemente elevata da consentirci di determinare la data di compilazione del catalogo. Quindi può avere senso definire il problema della stima di un possibile intervallo di datazione.
La seguente procedura che chiameremo statistica, sembra essere quella con una caratteristica più naturale e ovvia; si basa sull'ipotesi che le stelle con nome dell'Almagesto siano state misurate con una precisione latitudinale dichiarata di 10 minuti. Inoltre, basiamo la nostra ricerca sulle caratteristiche statistiche degli errori di gruppo riportate nel Capitolo 6. La procedura statistica di datazione è la seguente:
A. Specifichiamo il livello di confidenza 1 - ε.
B. Dopodiché prendiamo in considerazione il momento t e l'intervallo di confidenza Iγ(ε) per il complesso γstatZod A((t) dell'errore di gruppo nell'area Zod A. Quindi, per stimare il valore
Δ(t) = min Δ(t, γ, φ), (7.3.1)
dove il minimo viene preso per tutti i valori di γ in Iγ(ε) variando i valori di, mentre il valore di

definisce la discrepanza massima per tutte le stelle del kernel informativo calcolato per la presunta datazione t. I parametri (γ, φ) definiscono una certa rotazione della sfera celeste e ad onor del vero, lo fanno piuttosto arbitrariamente, vedere la Figura 3.14 (Capitolo 3).
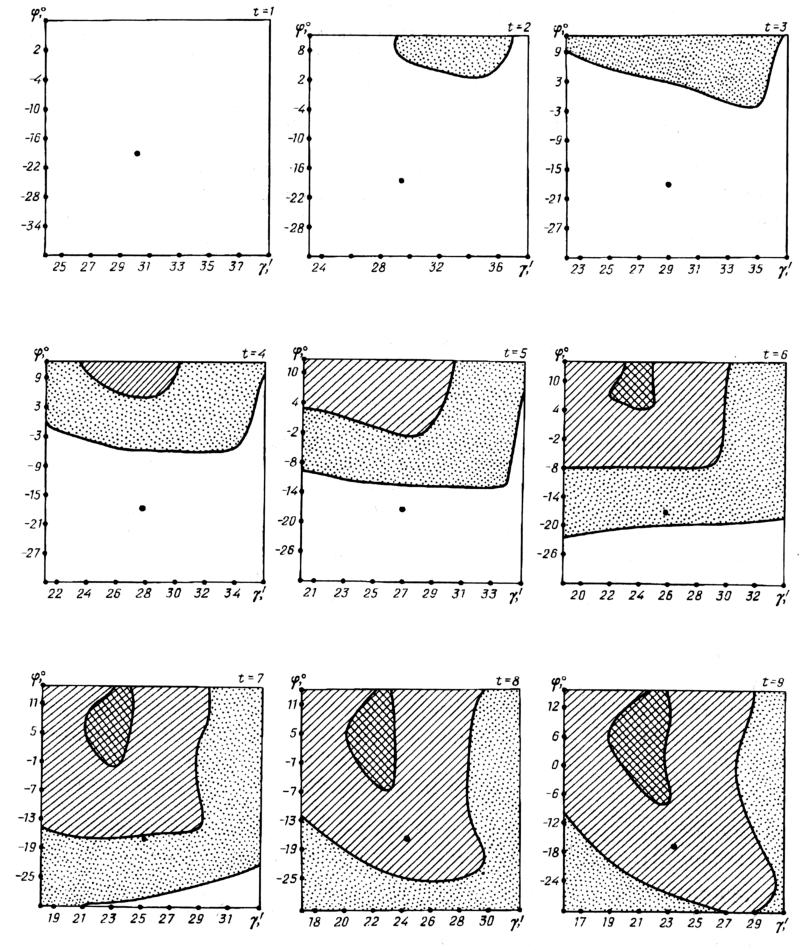
Figura 7.9.
Si può vedere la dipendenza Δ(t, γ, φ) per i valori temporali t che iniziano con 1, ovvero il 1800 d.C.
e terminano con t = 18, ossia il 100 a.C. L'area con la doppia ombreggiatura corrisponde a Δ ≤ 10'.
L'area con l'ombreggiatura singola corrisponde a 10'<Δ ≤ 15'.
L'area piena di puntini corrisponde a 15'<Δ ≤ 20'. Il punto grande corrisponde alle coppie dei parametri di γstatZod A(t) e φstatZod A(t).
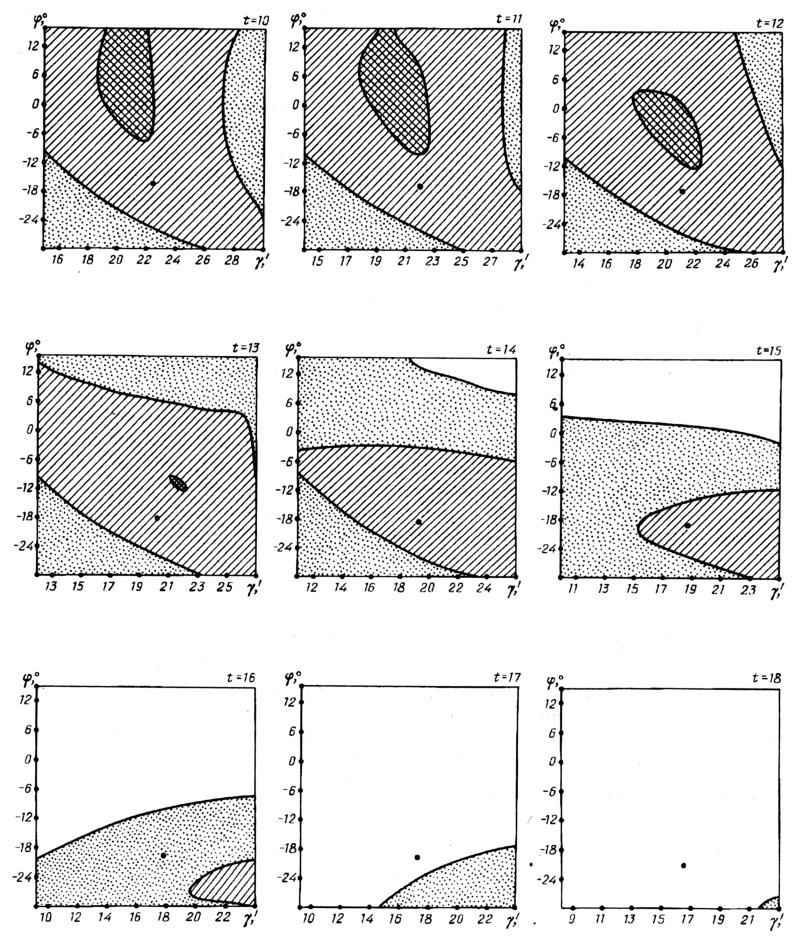
Figura 7.10.
Continuazione della figura precedente.
C. Se il valore edotto di Δ(t) non superasse di 10' il valore del tasso di precisione dichiarato del catalogo, il momento temporale t dovrebbe essere considerato come la possibile data di compilazione del catalogo. Altrimenti il catalogo non potrebbe essere datato nell'epoca t.
Ovviamente, il risultato derivante dall'applicazione di questa procedura di datazione dipende dalla scelta soggettiva del livello di confidenza 1 - ε. Pertanto, la sua stabilità dovrà essere verificata contro le variazioni di ε e sarà effettuata di seguito.
3.2. La dipendenza del minimax della discrepanza Δ per t, γ e φ dell’Almagesto.
Disegniamo il grafico delle 8 stelle con nome dell'Almagesto che formano il kernel informativo, per rappresentare la dipendenza del minimax della discrepanza latitudinale Δ(t, γ, φ) per tutte e tre le variabili. Questa dipendenza viene mostrata con una sequenza di diagrammi nelle Figure 7.9 e 7.10. Ogni diagramma corrisponde ad alcuni momenti fissi di t. I diagrammi sono stati indicati per t = 1,…, 18. Per gli altri valori di t i rispettivi diagrammi risultano nulli, come nel caso di t = 1. Ricordiamo ai lettori che t = 1 corrisponde al 1800 d.C. e t = 18 - all'inizio della nuova era. L'asse orizzontale dei diagrammi porta i valori di γ, quello verticale i valori di φ.
La doppia ombreggiatura segna le aree per le quali Δ(t, γ, φ) ≤ 10'.
Le aree ombreggiate corrispondono a 10' < Δ(t, γ, φ) ≤ 15'. L'area piena di puntini corrisponde a 15' < Δ(t, γ, φ) ≤ 20'.
Per il resto dei diagrammi, l'espressione Δ(t, γ, φ) > 2' è vera. In ogni diagramma i parametri γstatZod A(t), φstatZod A(t) sono stati contrassegnati da un punto grande.
I diagrammi dimostrano che la “zona” con doppia ombreggiatura che corrisponde alla discrepanza massima latitudinale di 10' per le otto stelle con nome dell'Almagesto, esiste solo per i momenti temporali che cadono nello spazio di 6 ≤ t ≤ 13, ovvero l'intervallo tra il 600 e il 1300 d.C.
L'area con l'ombreggiatura normale che corrisponde alla discrepanza latitudinale massima di 15' esiste solo per 4 ≤ t ≤ 16. Le dimensioni massime di queste aree vengono raggiunte in 7 ≤ t ≤ 12. Perché t > 18 sia un'alterazione accettabile dell'intervallo, l'area definita dai corrispondenti intervalli di confidenza non devono contenere punti in cui Δ(t, γ, φ) < 20'. Nello specifico, questo è vero per la datazione di Scaligero delle epoche in cui vissero Tolomeo e Ipparco. Inoltre, quando tentiamo di datare il catalogo dell'Almagesto al 100 d.C. o a un'epoca precedente, il minimax della discrepanza latitudinale Δ(t) risulta essere due volte maggiore della precisione dichiarata di 10 minuti per il catalogo dell'Almagesto. Per datazioni precedenti al 100 d.C., il valore di Δ(t) supera anche l'errore medio quadratico residuale per le stelle delle aree A, Zod A, B e Zod B, in quanto è vicino all'errore medio quadratico residuale dell'Almagesto per l'area celeste M, o piuttosto alle stelle fioche della Via Lattea (dove le osservazioni di tali stelle erano complicate per via delle tantissime stelle sullo sfondo che compromettevano la precisione, facendo uscire un tasso inaccettabilmente basso per le stelle luminose). Bisogna quindi respingere la datazione dell'Almagesto per l'epoca del 100 d.C. o prima, in quanto contraddicono il catalogo stellare.
Per cui, le Figure 7.9 e 7.10 dimostrano che l'area consentita dai valori di γ e φ, fondamentalmente non ci offre alcuna possibilità di calcolare la discrepanza latitudinale di tutte e 8 le stelle che formano il kernel informativo dell'Almagesto, con un valore inferiore a 10' per le epoche precedenti al 600 d.C. Se volessimo aumentare la soglia del tasso di errore a 15', la prima data possibile della Almagesto sarebbe il 300 d.C.
3.3. I risultati della datazione statistica del catalogo dell’Almagesto.
Assegniamo l'area di variazione St(α) del parametro γ nel modo seguente:
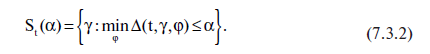
L'insieme St(α) potrebbe risultare ancora vuoto. Prendiamo in considerazione l'intersezione dell'insieme St(α) e l'intervallo di confidenza Iγ(ε) costruito attorno al valore di γstatZod A(t) Se questa intersezione non fosse vuota, potremmo dichiarare il momento t come la possibile epoca di compilazione del catalogo dell'Almagesto secondo la procedura di datazione statistica. Tutti questi momenti di t presi nel loro insieme, possono essere indicati come il possibile intervallo di datazione del catalogo dell'Almagesto.
Il risultato del calcolo di St(α) per l'Almagesto è rappresentato graficamente nella Figura 7.11. I puntini riempiono l'unione degli insiemi St(α) per α = 10'. Il margine circostante corrisponde al valore α = 15'. Troveremo un uso più avanti.
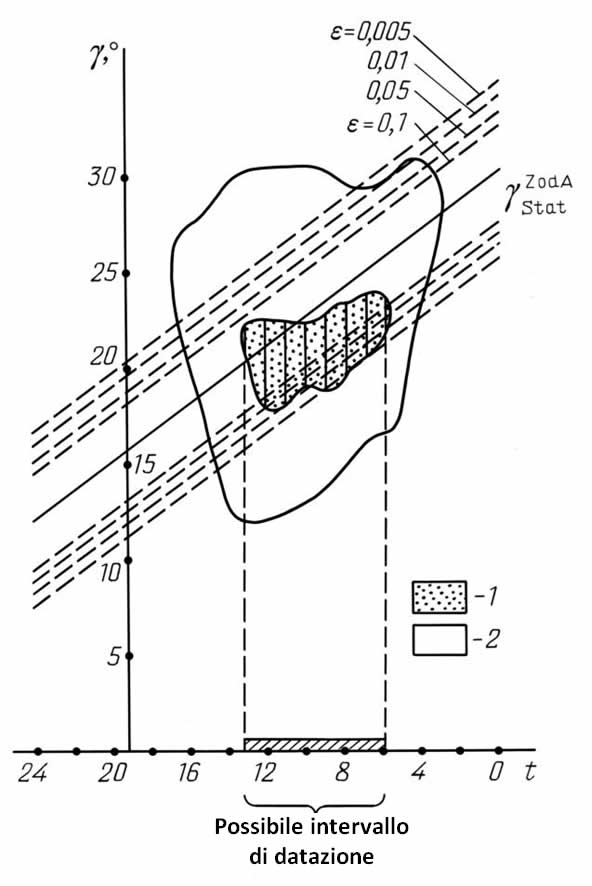
Figura 7.11.
Il risultato della procedura di datazione statistica applicata
al catalogo dell'Almagesto usando otto delle sue stelle con nome.
Il grafico della funzione γstatZod A(t) qui usata è stato calcolato nel Capitolo 6 (vedere la Figura 6.8). I valori degli intervalli di fiducia Iγ(ε) che corrispondono a valori diversi di ε, si trovano nella Tabella 6.3. La Figura 7.11 implica che il possibile intervallo di datazione è lo stesso per ε = 0,1, ε = 0,05, ε = 0,01 e ε = 0,005, ovvero 6 ≤ t ≤ 13. Se volessimo tradurre il risultato della datazione risultante in anni regolari, vedremmo che il possibile intervallo di datazione del catalogo dell'Almagesto inizia nel 600 d.C. e termina nel 1300 d.C.
3.4. La discussione del risultato.
La lunghezza del possibile intervallo di datazione del catalogo a cui siamo giunti è pari a 700 anni: 1300 - 600 = 700.
L'intervallo è piuttosto ampio per molti motivi. Abbiamo già menzionato il primo: la bassa precisione del catalogo dell'Almagesto, persino se accettassimo la precisione dichiarata di Tolomeo di 10'.
Questa bassa precisione rende impossibile datare il catalogo in un intervallo di tempo più ristretto, poiché persino la stella con nome più tra quelle prese in esame (Arturo) altera la sua latitudine di soli 10' ogni 260 anni.
Il valore è grande ed è ancora più grande per le altre stelle del kernel.
La seconda ragione deriva dal fatto che abbiamo utilizzato solo gli intervalli di confidenza del complesso degli errori di gruppo γ, dopo aver ridotto al minimo il valore Δ(t, γ, φ) tramite i vari possibili valori di φ, vedere le formule 7.3.1 e 7.3.2.
Questo approccio porta ovviamente all'ampliamento dell'intervallo di datazione del catalogo dell'Almagesto. Anzi, se potessimo considerare che φ è un errore di gruppo come γ, sceglieremmo il parametro φ dalla striscia di confidenza. Ciò aumenterebbe il valore di 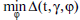 e quindi restringerebbe il possibile intervallo di datazione.
e quindi restringerebbe il possibile intervallo di datazione.
Tuttavia, come è stato sottolineato in precedenza, non abbiamo abbastanza motivi per considerare ϕ come un errore di gruppo nei gruppi stellari dell'Almagesto che abbiamo studiato.