CAPITOLO 8
L’angolo di inclinazione tra l’eclittica e l’equatore nell’Almagesto.
1. Il concetto tolemaico del valore dell’angolo di inclinazione dell’eclittica e l’errore sistematico γ.
L'angolo di inclinazione ε(t) tra l'eclittica e l'equatore è uno dei valori più importanti in astronomia. A prescindere dal metodo esatto utilizzato, per stimare le coordinate dell'eclittica delle stelle è necessario conoscere questo angolo. Si può usare l'astrolabio, come suggerisce il testo dell'Almagesto, oppure usare delle cosmosfere speciali per la conversione delle coordinate equatoriali, come veniva fatto nel Medioevo. Sono stati usati anche altri metodi, vedere il Capitolo 2 e l'Introduzione. È attualmente noto che l'angolo ε(t) varia nel corso del tempo a secondo della seguente regola:
ε(t) = 23° 27'8.2849" + 46.8093"t + 0.0059"t2 - 0.00183"t3,
dove t rappresenta il tempo contato in secoli a ritroso dal 1900 d.C. (vedere la formula 1.5.3).
Il testo dell'Almagesto contiene le descrizioni dettagliate di come misurare l'angolo ε, come anche gli strumenti effettivi che furono utilizzati per questo scopo, vedere il Capitolo I.12 dell'Almagesto ([1358]). Si afferma che queste misurazioni hanno portato al calcolo del valore di 2ε pari agli 11/83 di un cerchio completo, in termini moderni εA = 23° 51'20". Qui il valore di εA sta per il valore dell'angolo ε noto all'autore dell'Almagesto.
Mentre l'autore dell'Almagesto stava compilando il catalogo stellare, deve aver usato il valore conosciuto dell'angolo ε, annotandolo con il suo strumento (astrolabio, cosmosfera, ecc.). L'errore nella stima del valore reale di ε commesso dall'autore del catalogo, portò allo spostamento dell'intera sfera celeste per un certo angolo uguale al tasso di detto errore. In altre parole, l'errore commesso nella rappresentazione dell'angolo ε sullo strumento astronomico, porta all'errore sistematico inerente alle coordinate di tutte le stelle del catalogo o, più specificamente, alla parte del catalogo che è stata misurata con questo strumento. È abbastanza facile da capire che un errore sistematico di questo tipo influenza principalmente le latitudini delle stelle. Si tratta proprio dell'errore sistematico che abbiamo edotto nel Capitolo 6, quando stavamo provando a calcolare γstat(t) per i diversi valori di t. La dipendenza temporale dell'errore è definita principalmente dal valore reale dell'angolo ε(t), che cambia gradualmente nel corso del tempo. Questa alterazione è uniforme e praticamente lineare entro i confini dell'intervallo temporale scelto a priori di 0 ≤ t ≤ 25.
Quando l'autore del catalogo stellare dell'Almagesto commise un errore nella determinazione e nella fissazione dell'angolo ε con il suo strumento, modificò il valore di ε rendendolo più grande o più piccolo del valore reale; quindi il catalogo potrebbe guadagnare o perdere anni di età in base all'inclinazione dell'eclittica rispetto all'equatore. Qualunque di queste possibilità potrebbe diventare reale con una probabilità dello 0.5. Ciò che osserviamo di fatto è la manifestazione dell'opzione più probabile, vale a dire che il valore di ε rappresentato dal catalogo dell'Almagesto è uguale al valore reale di ε(t) per l'epoca approssimativa del 1200 a.C., vedere il Capitolo 6. Il compilatore dell'Almagesto fece così diventare il catalogo stellare di gran lunga più vecchio.

Figura 8.1.
La striscia di confidenza γstat(t) ±Δγ stimata per Zod A:
l'insieme dei possibili valori di γgeom(t per la procedura geometrica di datazione,
come pure il grafico delle dipendenze per la deviazione ε = εA
indicata nell'Almagesto e il valore reale di questo angolo.
Supponiamo che il catalogo dell'Almagesto sia stato compilato nel momento temporale t e che il suo autore abbia considerato un angolo di inclinazione tra l'eclittica e l'equatore pari a 23°51'20", che è il valore dichiarato nell'Almagesto. Supponiamo anche che il compilatore del catalogo abbia cercato di fissare questo valore dell'angolo sul suo strumento astronomico progettato per la stima (tramite l'osservazione diretta o il ricalcolo) delle coordinate stellari dell'eclittica. Se dovessimo considerare che il valore dell'errore dell'osservatore rientra nell'intervallo consentito di ±Δε definito dalla precisione di fabbricazione dello strumento, l'errore sommario dell'angolo ε fissato dallo strumento sarebbe uguale a
εA – ε(t) ± Δε = 23°51'20" – ε(t) ± Δ(ε).
Confrontiamo il valore di questo errore con la striscia di confidenza γstat(t) ±Δγ, dell'errore sistematico γ, come pure l'insieme di γ per il quale è possibile sovrapporre la configurazione stellare del kernel informativo dell'Almagesto con la corrispondente configurazione stellare calcolata e con un tasso garantito di precisione latitudinale pari a 10', vedere il Capitolo 7 che ci dice anche che l'ultimo insieme non è vuoto per tutti gli intervalli tranne 6 ≤ t ≤ 13. Cerchiamo di scegliere i valori stimati dall'area celeste Zod A per γstat(t) poiché, come è stato affermato in precedenza, la parte Zod A del catalogo dell'Almagesto possiede un unico errore sistematico γ. La striscia di confidenza di γ è più stretta in questa parte del catalogo; inoltre, tutte le stelle del kernel informativo o si trovano in Zod A o nelle sue immediate vicinanze, vedere il Capitolo 7.
Tabella 8.1. Le lunghezze dell'arco di 2,5', 5', 10' e 1° in millimetri, come indicate sugli anelli il cui raggio è uguale a 50 cm, 75 cm e 1 m. |
|||
| Arco | La lunghezza dell'arco (lunghezza dell'anello) in millimetri a seconda del raggio dell'anello in metri | ||
| 0.5 (3.14) | 0.75 (4.71) | 1.0 (6.28) | |
| 2’30” | 0.4 | 0.5 | 0.7 |
| 5’ | 0.7 | 1.1 | 1.4 |
| 10’ | 1.5 | 2.2 | 2.9 |
| 1° | 8.7 | 13.0 | 17.5 |
Nella Figura 8.1 possiamo vedere la striscia di confidenza γstat(t) ±Δγ stimata nella zona celeste Zod A con un livello di confidenza di 0.998. Possiamo anche vedere l'insieme dei valori accettabili di γgeom(t) relativi alla procedura di datazione geometrica per i quali la discrepanza latitudinale massima delle stelle del kernel informativo dell'Almagesto non supera i 10', vedere il Capitolo 7. Infine, nella Figura 8.1 vediamo il grafico delle dipendenze per l'aberrazione di ε = εA come determinata nell'Almagesto dal valore reale di questo angolo: γAlm(t) = εA - ε(t).
La Figura 8.1 dimostra che il grafico di γAlm(t) è molto vicino all’area “geometricamente valida” (γ, t)geom e alla striscia di confidenza che circonda γstat(t), anche se non lo attraversa; ciò avverrebbe se trasponessimo il grafico di γAlm(t) verso l’alto di circa 2,5’;. Inizierebbe ad incrociare automaticamente sia la striscia di confidenza che l’area “geometricamente valida” che si è spostata verso il margine della striscia di confidenza. Uno spostamento di 6,5’ verso l’alto farà spostare il grafico di γAlm(t) fino a farlo praticamente coincidere con il grafico di γstat(t), mentre sta ancora attraversando l’area “geometricamente valida”. Il valore dello spostamento necessario per questo scopo corrisponde alla variazione consentita di Δε con εA fissato sullo strumento, dandoci solo l’idea di quanto siano stati precisi i produttori dello strumento astronomico. La Tabella 8.1 contiene i valori della lunghezza dell’arco di 2,5’, 5’, 10’ e 1° (in mm.) per uno strumento astronomico (astrolabio, cosmosfera, ecc.) con un raggio di 50 cm, 75 cm e 1 m.
Dalla Tabella 8.1 possiamo vedere che per fissare l'angolo ε dell'errore Δε dello strumento astronomico, il valore di 2,5' - 5' è molto reale per il Medioevo. Corrisponde alla gamma di fluttuazione della dimensione lineare di un mero 0,5 - 1 mm.
Pertanto, i valori di inclinazione dell'eclittica che abbiamo scoperto nel catalogo dell'Almagesto corrispondono al valore di εA contenuto nel testo dell'Almagesto.
2. Lo Zodiaco e la curva sinusoidale di Peters.
Paragrafo 1. Il libro di Peters e Knobel([1339]) contiene un importante grafico di discrepanza che Peters ottenne dalla sua analisi del catalogo dell'Almagesto. La curva sinusoidale di questo grafico viene chiamata la “curva sinusoidale latitudinale di Peters” (vedere [1339], pagina 6). Questa curva indica la presenza di alcuni errori sistematici nell'Almagesto.
In questo paragrafo spieghiamo perché la “curva sinusoidale di Peters” è inerente al catalogo dell'Almagesto.
Paragrafo 2. Consideriamo la posizione dell'eclittica Π per t = 18, ovvero il 100 d.C. Sopra ci segniamo il punto Q(18) dell'equinozio di primavera. Procediamo nel dividere l'eclittica in 360 gradi usando come riferimento iniziale il punto dell'equinozio di primavera, vedere la Figura 8.2.
Ora segniamo le posizioni delle stelle effettive per il 100 d.C. con dei puntini neri sulla sfera celeste e le posizioni delle stesse stelle nell'Almagesto con dei puntini bianchi. Le coppie dei rispettivi puntini (quello bianco e quello nero) nella Figura 8.2 sono collegate insieme con dei segmenti, in modo da far vedere bene le corrispondenze.
Possiamo calcolare la differenza latitudinale per ciascuna di quelle coppie, in altre parole la loro discrepanza latitudinale. Per cui stiamo calcolando la differenza tra la latitudine della stella i nell'Almagesto e la vera latitudine di questa stella per il 100 d.C. In [1339] Peters ha studiato le stelle zodiacali dell'Almagesto da questa posizione. Tuttavia, pare che ne abbia persa qualcuna. L'Almagesto contiene un totale di 350 stelle zodiacali. Come è già stato detto in [1339] pagina 17, Peters scelse solo 218 stelle per il suo studio delle longitudini delle stelle zodiacali, senza specificare i principi della selezione. L'esatta quantità delle stelle studiate da Peters nel suo studio delle latitudini non è stata riportata da nessuna parte in [1339], ma si può presumere che abbia preso le stesse stelle che usò nello studio delle longitudini.
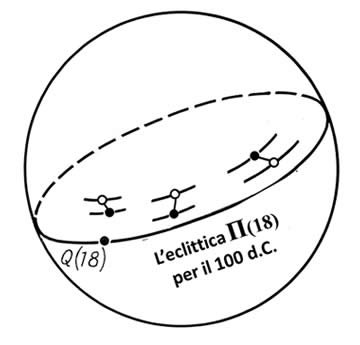
Figura 8.2.
Il confronto della posizione delle stelle reali del 100 d.C.
con la loro posizione indicata nell'Almagesto.
Calcoliamo le discrepanze latitudinali per tutte le stelle dell'elenco zodiacale e le rappresentiamo sul grafico. Occorrerà prendere la longitudine delle stelle e segnarla sull'asse orizzontale, dopodiché presentare il valore della discrepanza latitudinale su quello verticale. Tutto questo si tradurrà in un certo agglomerato di puntini disegnati sul piano che chiameremo “campo di errore”. Una volta che avremo diviso la scala longitudinale in segmenti di 10 gradi e avremo calcolato la media di ognuno, potremo costruire la curva di lisciamento mostrata nella Figura 8.3. A sua volta, questa curva potrà essere approssimata dalla curva sinusoidale ottimale secondo il criterio del minimo della discrepanza media quadratica.
Una procedura simile può essere eseguita per le longitudini. Come conseguenza giungeremo a un'altra curva di lisciamento, che nella Figura 8.3 è stata rappresentata con una curva punteggiata. Ne parleremo più avanti, ora cerchiamo di trovare una spiegazione ovvia a queste curve.
Paragrafo 3. Cominciamo con lo studio della curva sinusoidale latitudinale di Peters. Dobbiamo far notare il meccanismo naturale che ci consente di spiegare l'inclusione degli errori sistematici nelle latitudini delle stelle zodiacali. Si tratta dell'errore nella posizione del piano dell'eclittica dell'osservatore rispetto a quello dell'eclittica effettiva per il momento dell'osservazione che non ci è noto a priori.
Ritorniamo alla nostra considerazione dell'eclittica Π(t0) per il momento di osservazione t0. Il punto dell'equinozio Q(t0) è stato segnato nella Figura 8.4 come l'inizio delle coordinate. Prima abbiamo visto il campo dell'errore latitudinale per t = 18. Facciamo lo stesso per il momento t0 riguardo l'osservazione delle stelle del catalogo dell'Almagesto e disegniamo il corrispondente campo di errore latitudinale nella Figura 8.5. La curva di lisciamento sarà segnata con c(X, K (t0, 0, 0), vedere la curva tratteggiata nella Figura 8.5. Spieghiamo questa indicazione. Come detto sopra, la X viene usata per fare riferimento al catalogo dell'Almagesto. K(t, β, γ) è usata per riferirsi al catalogo reale K(t) indicando le posizioni delle stelle effettive per l'epoca perturbata dai parametri β e γ, vedere il Capitolo 6. Pertanto, K(t0, 0, 0) è un catalogo che non è stato soggetto alla perturbazione casuale che mostra le posizioni effettive delle stelle per il momento dell'osservazione t0 che non conosciamo a priori.
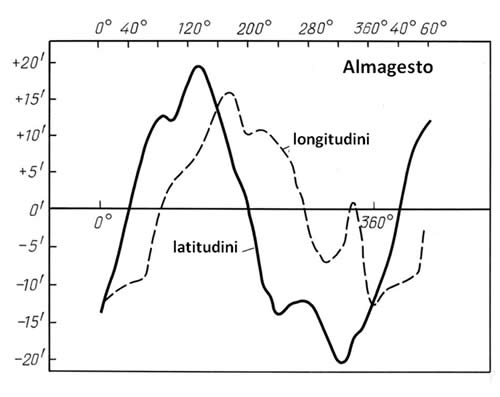
Figura 8.3.
Le curve di lisciamento di Peters per il 100 d.C. (latitudinale e longitudinale).
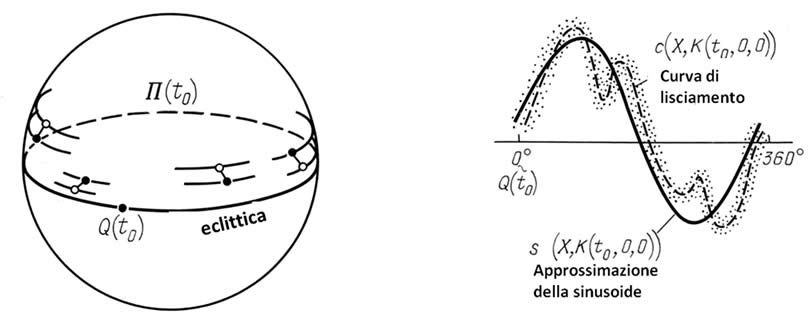
Il sistema per il conteggio degli errori latitudinali.
La curva tratteggiata indica la curva di lisciamento c(X, K(t0, 0, 0).
La curva continua è l'approssimazione della sinusoide s(X, K(t0, 0, 0).
Abbiamo già spiegato nel Capitolo 6 che per poter trovare la rotazione eclittica ottimale nel senso della media quadratica, dobbiamo risolvere il problema della corrispondente regressione. A tal fine, come famiglia di curve in approssimazione dovremo utilizzare una famiglia sinusoidale a due parametri. Il primo parametro di questa famiglia deve essere definito dall'amplitudine della curva sinusoidale, mentre il secondo dalla sua fase. Abbiamo risolto questo problema nel Capitolo 6, sia per l'Almagesto in generale che per le sue diverse parti nello specifico; tra le ultime, lo zodiaco che ci interessa al momento. Definiamo la curva sinusoidale ottimale in approssimazione con s(X, K(t, 0, 0)), vedere la curva continua nella Figura 8.5. I parametri della curva sinusoidale saranno definiti con A* (amplitudine) e φ* (fase).
L’eclittica dell’osservatore, l’eclittica effettiva e l’eclittica dell’osservatore.
L’alterazione della fase sinusoidale.
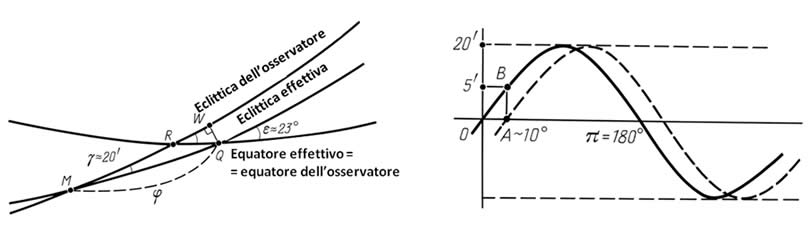
Paragrafo 4. Sarebbe una buona idea quella di discutere il concetto di approssimazione della fase della curva sinusoidale. La cosa importante è che la fase sia stimata con un tasso di precisione di 15 gradi al massimo. Forniamo due spiegazioni praticamente identiche a questo fatto. La prima si basa sull'analisi del modo in cui l'errore dell'osservatore nella stima del piano dell'eclittica influenza la fase di approssimazione della curva sinusoidale. Si possono vedere i seguenti oggetti nella Figura 8.6. Innanzitutto, l'equatore effettivo per il momento di osservazione t0. Come abbiamo già spiegato in precedenza, questo equatore può essere considerato quasi identico all'equatore dell'osservatore. In secondo luogo, l'eclittica effettiva per il momento t0 e l'eclittica dell'osservatore.
Sappiamo che l'angolo tra l'eclittica dell'osservatore e l'eclittica effettiva equivale approssimativamente a 20', che è l'errore γ dell'osservatore. L'angolo tra l'equatore e l'eclittica è pari a ε, ossia circa 23°. Non importa quale delle eclittiche prendiamo in considerazione in questo momento, poiché l'angolo tra di loro è piccolo rispetto ai 23°. L'arco nella Figura 8.6 rappresenta l'errore dell'osservatore nella stima del punto dell'equinozio primaverile. Come già sappiamo, questo errore è più o meno pari a 10', che è il valore della scala graduata del catalogo dell'Almagesto. Supponiamo che l'arco RQ sia più o meno uguale a 10'; in questo caso la distanza dall'arco WQ sarà più o meno pari a 10' × sin20°, ovvero circa 5'. In questo caso, la distanza dall'arco φ, ossia l'arco MQ della Figura 8.6, sarà uguale a circa 5' / sin20', ovvero circa 15°. Tutto ciò che dobbiamo dire è che l'arco MQ ci offre una rappresentazione precisa della fase di approssimazione della curva sinusoidale. Stiamo contando la fase della curva sinusoidale che inizia con il punto dell'equinozio di primavera Q(t) sull'eclittica effettiva Π(t).
Pertanto, le numerose piccole perturbazioni nella stima dell'eclittica da parte dell'osservatore, disturbano la fase della curva sinusoidale per un fattore di diversi gradi, rendendola “instabile”. Lo stesso fenomeno riceverebbe una spiegazione, qualora fosse considerato come parte della curva di lisciamento c(X,K(t, 0, 0)) il problema dell’approssimazione con la curva sinusoidale ottimale s(X, K(t, 0, 0)).
L'approssimazione della curva di lisciamento per mezzo della curva sinusoidale ottimale ci fa arrivare al valore minimo del possibile errore medio quadratico. Si deve consentire una certa variazione di questo minimo, per il fatto che i parametri ottimali della curva sinusoidale in linea generale non riescono a concordare precisamente con l'effettivo errore di osservazione. Consentendo delle variazioni di 5 minuti nel punto minimo di aberrazione media quadratica, dobbiamo notare che la fase di variazione di 10 gradi della curva sinusoidale con un'amplitudine di 20', cambia l'ordine di qualsiasi punto della curva sinusoidale per un massimo di 5'. Per una curva sinusoidale standard con un'amplitudine di 1 e una fase 0 disegnata come una curva continua nella Figura 8.7, i segmenti OA saranno più o meno uguali all'arco OB, dal momento che ora stiamo considerando il segmento relativamente piccolo OA, ossia quello pari a 1/6 radianti (10 gradi). In questo caso il segmento AB comprende 1/6 dell'amplitudine, ossia circa 3.3'. Pertanto, una perturbazione di tre minuti della discrepanza media quadratica può provocare una fase di alterazione di 10 gradi della curva sinusoidale ottimale in approssimazione.

Figura 8.8.
L'Almagesto, t = 9. La curva tratteggiata rappresenta
la sinusoide iniziale di Peters,
mentre la curva continua rappresenta la stessa cosa dopo
la sottrazione del valore dell'errore sistematico.
Paragrafo 5. Nei capitoli precedenti abbiamo già stimato il possibile intervallo di datazione del catalogo dell'Almagesto, vale a dire che abbiamo scoperto che t0 si trova sull'intervallo tra 6 e 13, ossia circa il 600 d.C. e il 1300 d.C. Pertanto, sarebbe particolarmente interessante studiare le curve sinusoidali in approssimazione s(X,K(t, 0, 0)) per questo intervallo di possibili datazioni. E' risultato che all'interno dell'intervallo tra il 600 d.C. e 1300 d.C. non si alterano troppo, ovvero dimostrano di essere scarsamente dipendenti da t0. Più precisamente, l'amplitudine massima di A* cambia da 26' per t0 = 6 a 20' per t0 = 13 nell'intervallo tra il 600 d.C. e 1300 d.C. Le fasi corrispondenti degli spostamenti di φ* hanno luogo tra i valori di 17° e 18° in relazione al corrispondente punto equinoziale Q(t0) sull'eclittica Π(t0). Pertanto possiamo prendere in considerazione qualsiasi curva di lisciamento c(X, K(t0, 0, 0)) come “tipica rappresentante” di classe, dove t0 può assumere qualsiasi valore compreso tra 6 e 13. Sarebbe ovvio considerare la metà dell'intervallo temporale, vale a dire il valore di t0 = 9.
Dimostriamo in che modo la curva di lisciamento c(X,K(t0, 0, 0)) guardi t0 = 9 prima e dopo la sottrazione ottimale della curva sinusoidale, in altre parole prima e dopo l'esclusione degli errori sistematici che abbiamo scoperto. Nella Figura 8.8 si può vedere che la curva di lisciamento c(X, K(t0, 0, 0)) è vicina alla curva sinusoidale per t0 = 9. I parametri della curva sinusoidale ottimale per t0 = 9 sono i seguenti: l'amplitudine è uguale a 24', mentre la fase a 17°. Nella Figura 8.8 la curva di lisciamento è stata disegnata con una curva tratteggiata. L'esclusione dell'errore dell'osservatore riguardo la stima dell'eclittica dal catalogo X, è equivalente alla sottrazione delle curve sinusoidali ottimali con i parametri A* = 24' e φ* = –17° per t0 = 9. Di conseguenza, nella Figura 8.8 la curva di lisciamento della discrepanza latitudinale assume la forma di una curva continua. Si può vedere chiaramente la differenza tra la curva punteggiata e la curva continua; quest'ultima fluttua attorno all'asse dell'ascissa e corrisponde all'errore medio pari a zero dell'osservatore nella stima della posizione dell'eclittica. È ovvio che il campo di errore ora è approssimato da una curva sinusoidale degenerata, ossia da una semplice linea retta che si sovrappone all'ascissa.
Conclusione. La compensazione degli errori dell'osservatore sul possibile intervallo di datazione scoperto nel catalogo dell'Almagesto, ovvero il 600-1300 d.C., risulta quando scompaiono quegli effetti come le curve sinusoidali latitudinali di Peters.
Paragrafo 6. Torniamo alla curva sinusoidale di Peters nelle latitudini del catalogo dell'Almagesto. Dal momento che nei suoi calcoli è possibile che Peters non abbia tenuto conto di tutte le stelle zodiacali, abbiamo ricalcolato e costruito un grafico simile a quello di Peters per t = 18, ossia il 100 d.C., vedere la Figura 8.3. Abbiamo considerato tutte le stelle zodiacali dell'Almagesto tranne alcuni refusi con una discrepanza latitudinale superiore a 1,5°. I dati sono stati presi da [1339]. Abbiamo analizzato quasi tutte le 350 stelle zodiacali dell'Almagesto.
Il risultato dei nostri calcoli lo potete vedere nelle Figure 8.9 e 8.10 insieme al campo di errore latitudinale dello zodiaco dell'Almagesto per t = 18. Questo campo è costituito da 350 punti sparsi su un piano. Lo zigzag continuo rappresenta la curva di lisciamento c(X, K(t0,0, 0)). È chiaramente visibile che qualitativamente assomiglia alla curva di Peters nella Figura 8.3. In linea generale, il comportamento della nostra curva adattata nella Figura 8.9 è simile a quello della curva di Peters nella Figura 8.3. Tuttavia, ci sono alcune lieve differenze che a quanto pare possono essere spiegate dal principio di selezione della stella zodiacale usata da Peters, che a noi rimane sconosciuto.
Nella Figura 8.10 si può anche vedere la curva sinusoidale ottimale s(X,K(18, 0, 0)). I suoi parametri sono i seguenti: amplitudine 16' e fase 22°, vedere il Capitolo 6.
Paragrafo 7. Prima abbiamo considerato le diverse proprietà del campo di errore latitudinale rispetto al vero momento di osservazione t0. Esaminiamo ora lo stesso campo per il momento arbitrario t che non coincide con t0. Possiamo vedere quanto segue nella Figura 8.11:
- L'eclittica effettiva (t) per il momento di osservazione t0.
- L'eclittica dell'osservatore è rappresentata da una curva punteggiata e non è uguale a Π(t0) a causa degli effetti dell'errore nell'osservazione commesso dal compilatore del catalogo dell'Almagesto.
- L'eclittica effettiva Π(t) per qualsiasi altro momento fisso di t.
I punti dell'equinozio di primavera Q(t0) e Q(t) vengono disegnati sulle eclittiche Π(t0) e Π(t). Il punto N corrisponde all'incrocio di dette eclittiche. La distanza tra il punto M e l'eclittica Π(t) è piuttosto piccolo, vale a dire che non supera i 20' se |t - t0| non supera i 2000 anni. Pertanto, il campo di errore latitudinale correlato all'eclittica Π(t) dovrebbe essere approssimato alla somma delle due curve sinusoidali. Il primi risulta dall'errore nell'osservazione commesso nel momento t0 ed è stato discusso nei dettagli in precedenza.
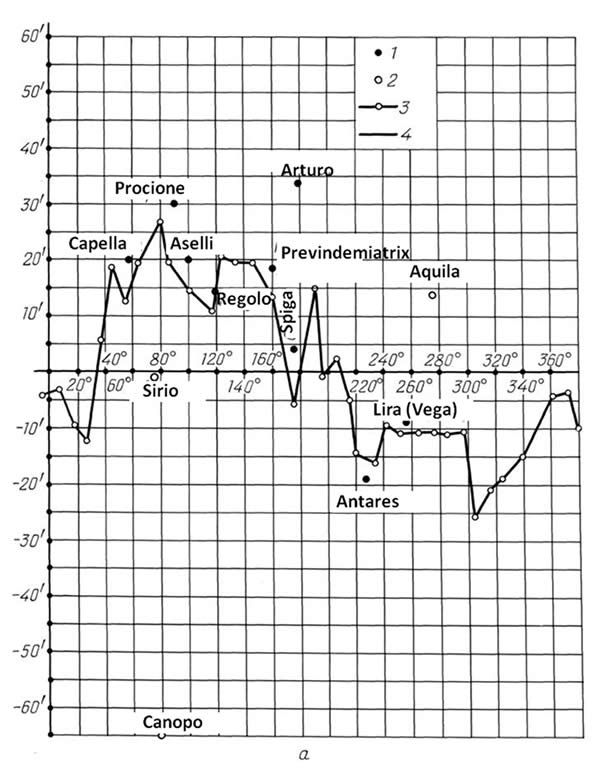
Figura 8.9.
La curva di Peters che abbiamo calcolato per lo Zodiaco dell'Almagesto, t = 18.
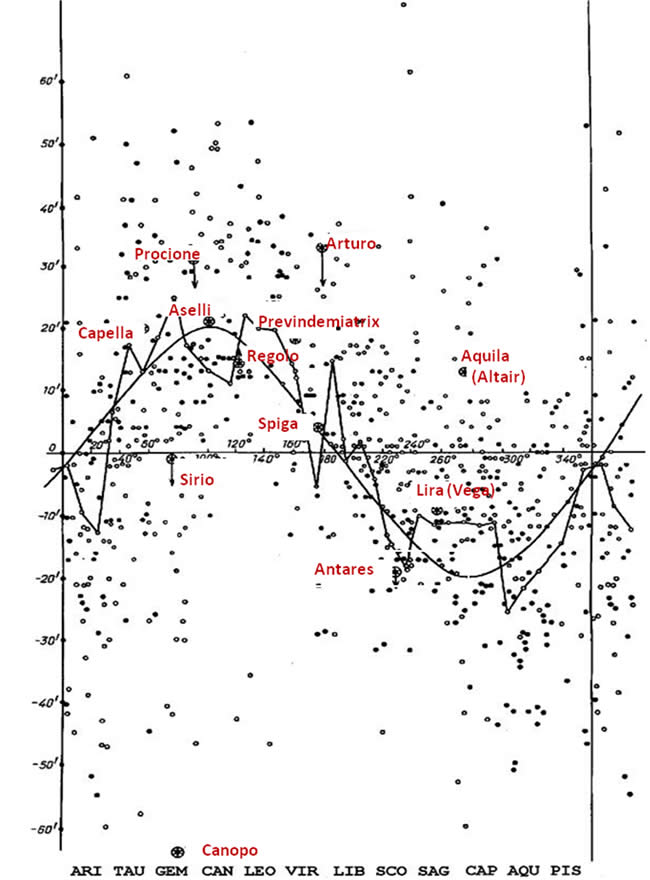
Figura 8.10.
Il campo di errore per lo Zodiaco dell'Almagesto, t = 18. Le stelle zodiacali sono rappresentate dai puntini neri, le altre da quelli chiari. Lo zigzag è la curva di Peters approssimata agli intervalli di 10 gradi, mentre la curva liscia rappresenta la sinusoide ottimale.
La fase di questa curva sinusoidale correlata al punto Q(t) dell'equinozio di primavera sull'eclittica D(t), equivale più o meno alla somma della sua fase correlata al punto di equinozio di primavera Q(t0), vedere l'arco MQ(t0) nella Figura 8.11 e la distanza dell'arco RQ(t). Stiamo parlando di una somma algebrica, ossia di una somma con un valore positivo o negativo. L'arco RQ(t) è uguale al valore di precessione per il tempo t - t0.
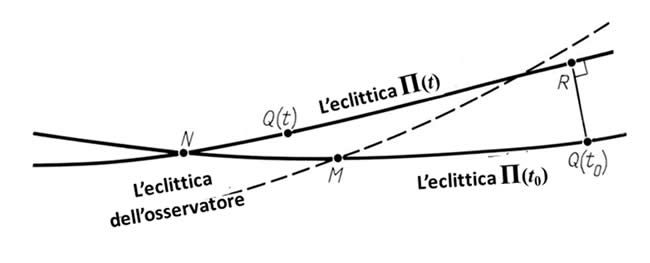
Figura 8.11.
La eclittica effettiva per il momento dell'osservazione, l'eclittica dell'osservatore e la posizione della eclittica effettiva
per un momento diverso nel tempo.
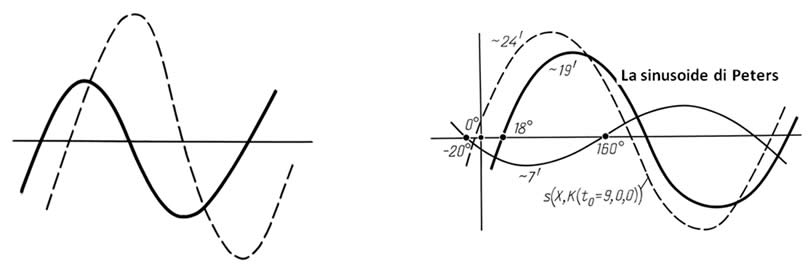
Una coppia di curve sinusoidali la cui somma definisce
approssimativamente il campo di errore latitudinale.
La somma delle due sinusoidi produce la sinusoide di Peters
(la curva in grassetto).
La seconda curva sinusoidale st, t0 rappresentata nella Figura 8.12 con una curva continua, risulta dalla discrepanza tra l'eclittica Π(t) e l'eclittica Π(t0). Ha un'amplitudine approssimativa di 47"/ |t - t0|, vedere [1222] o il Capitolo 1. La sua fase viene stimata dalle formule della precessione prese dal paragrafo 5 del Capitolo 1, che originariamente furono prese da [1222].
La curva di approssimazione risultante rappresenta la somma di queste due curve sinusoidali. Questa curva ha un solo massimo locale e un solo minimo locale sulla circonferenza, ossia l'eclittica.
Ciò implica la seguente semplice dichiarazione. Prendiamo in considerazione i due momenti temporali t0 e t. Quindi la curva di lisciamento c(X, K(t0, 0, 0)) deve più o meno coincidere con la somma delle due curve c(X, K(t, 0,0)) ≈ c(X, K(t0, 0, 0)) + st, t0. Per cui, possiamo affermare che una curva sinusoidale come quella di Peters per il momento temporale t è prossima alla somma della curva sinusoidale simile per il momento t0 e a quella corrispondente alla rotazione dell'eclittica nel tempo t - t0 (tra t0 e t). Questa è una dichiarazione generale valida per tutte le coppie di t e t0.
Paragrafo 8. Consideriamo ora la curva risultante di approssimazione per il 100 d.C., ossia t = 18. Abbiamo appena spiegato che per questo scopo bisogna sommare le due curve sinusoidali. La prima corrisponde al momento effettivo dell'osservazione t0, mentre la seconda al momento t per cui è stata calcolata la risultante curva di approssimazione. Scegliamo t0 = 9 come il “tempo effettivo di osservazione”, ossia il 1000 d.C. circa. Questo valore di t0 è a metà del possibile intervallo di datazione del catalogo dell'Almagesto che abbiamo scoperto tra il 600 e il 1300 d.C., ovvero t = 13 e t = 6. La prima curva sinusoidale (vedi la curva tratteggiata nella Figura 8.13) ha un'amplitudine di 24' e una fase di 5°, che è la somma di -17° (vedi l'arco MQ(t0) nella Figura 8.11) con i 12° della precessione per circa 900 anni.
La seconda curva sinusoidale (vedere la curva continua fine nella Figura 8.13) corrisponde alla scelta del momento t = 18, ossia il 100 d.C., vedi sopra. La sua amplitudine equivale approssimativamente a 47" × 9 ≈ 7', vedi sopra, e la sua fase è prossima a 160°, vedi il Capitolo 1. Sul frammento tra –20° e 160° mostrato nella Figura 8.13, questa curva si trova sotto l'ascissa o ha un valore negativo. Sommando le due curve sinusoidali otterremo la risultante curva di approssimazione disegnata con una curva continua in grassetto nella Figura 8.13.
Pertanto, la curva sinusoidale della discrepanza latitudinale scoperta da Peters, partendo dal presupposto che il catalogo dell'Almagesto sia stato compilato nel 100 d.C., è la somma di due curve sinusoidali, vale a dire la curva sinusoidale del momento di osservazione risultante da una stima errata della posizione dell'eclittica da parte dell'osservatore, e la curva sinusoidale che risulta dall'angolo tra l'eclittica del 100 d.C. e l'eclittica del tempo di osservazione.
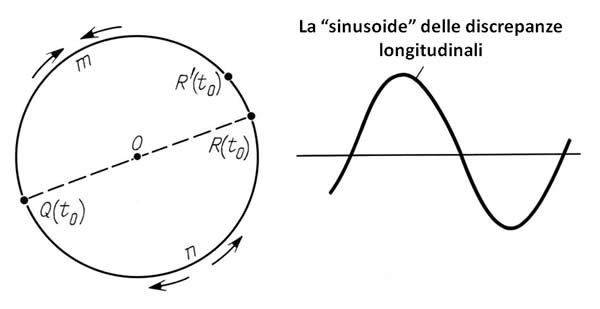
Figura 8.14.
Il grafico della discrepanza longitudinale delle stelle zodiacali.
Paragrafo 9. Concludiamo con la rotazione della curva sinusoidale longitudinale di Peters (vedere la curva tratteggiata nella Figura 8.3). Il meccanismo sopra descritto spiega la genesi della curva sinusoidale latitudinale. Tuttavia, è molto difficile che influenzi le longitudini delle stelle zodiacali. Pertanto, la stima errata dell'eclittica dell'osservatore non provoca il manifestarsi della curva sinusoidale longitudinale. Ciò nonostante, possiamo assistere a una debole manifestazione della curva sinusoidale che appare anche nelle longitudini. Supponiamo che l'osservatore medievale abbia fatto un errore nella stima dei punti equinoziali di primavera e autunno, o che abbia misurato le coordinate delle stelle di base con insufficiente precisione, che poi è la stessa cosa. Tenete presente che a differenza delle latitudini che sono state sempre contate dall'anello ellittico dello strumento astronomico, fissato nella costruzione con un errore permanente, le longitudini stellari sono state contate partendo da diverse stelle luminose. Altrimenti si sarebbero dovuti misurare degli angoli più grandi di 180°, che è una procedura molto ardua (vedere i Capitoli VII.3 e VII.4 dell'Almagesto ([1358])). Questa circostanza è illustrata nella Figura 8.14.
La mancanza di precisione nella stima dei punti equinoziali da parte dell'osservatore, porterà di fatto alla divisione dell'eclittica in due parti disuguali per i punti Q(t0) e R'(t0). Qui, R'(t0) sta per la posizione errata del punto equinoziale d'autunno, mentre R(t0) il vero punto equinoziale d'autunno. La lunghezza dell'arco RR' può essere piuttosto piccola, circa 10' - 15', rimanendo quindi entro la soglia di precisione dell'Almagesto. Alcune longitudini zodiacali potrebbero essere state misurato dal punto Q dell'equinozio di primavera, ovvero da un certo gruppo di stelle di base, mentre altre dal punto R dell'equinozio d'autunno, ossia da un altro gruppo di stelle di base. Di conseguenza, le longitudini stellari sul segmento QmR' saranno “compresse” più o meno di 15', mentre sul segmento QnR' al contrario saranno ampliate di circa 15'. Pertanto, calcolando il grafico della discrepanza longitudinale delle stelle zodiacali finiremo con una curva sinusoidale, vedere la Figura 8.14. Tenete presente il valore relativamente piccolo dell'errore, 10' - 15', che è l'amplitudine della curva sinusoidale longitudinale di Peters mostrata nella Figura 8.3.