CAPITOLO 9
L’applicazione del nostro metodo per la datazione degli altri cataloghi medievali
1. Introduzione.
In precedenza abbiamo descritto i metodi di analisi statistica e di datazione dei cataloghi stellari, per poi applicarli al catalogo dell'Almagesto. Sarebbe interessante applicare gli stessi metodi alla datazione degli altri cataloghi compilati con l'ausilio di strumenti simili a quelli di Tolomeo, ovvero l'osservazione ad occhio nudo.
Il presente capitolo contiene lo studio dei cataloghi stellari compilati da Ulugbek, Al-Sufi, Tycho Brache ed Hevelius. Il catalogo di Al-Sufi si è rivelato essere un semplice clone dell'Almagesto. Tuttavia, la cosa è già stata fatta notare da diversi osservatori, vedere ad esempio [1339], [1119] e [1120]. A quanto pare siamo i primi ad aver condotto un'analisi statistica approfondita degli errori nella latitudine stellare dei cataloghi di Ulugbek, Tycho Brahe ed Hevelius. La precisione di questi cataloghi si è rivelata essere molto peggio di quel che credevamo, vedere di seguito. La discrepanza maggiore è nel catalogo di Hevelius, nientemeno che un fattore di 100x o 200x.
Per primi abbiamo datato i cataloghi di Tycho Brahe e Ulugbek. La datazione delle osservazioni di Tycho Brahe si presume che sia nota: il 1570-1600 d.C. Il nostro metodo produce una datazione del catalogo di Tycho Brahe che concorda abbastanza bene con questo periodo.
Nel caso del catalogo di Ulugbek, il possibile intervallo che abbiamo calcolato copre anche la datazione di Scaligero, vale a dire il 1437 d.C. Tuttavia, questo intervallo si interseca anche con il possibile intervallo di datazione calcolato per il catalogo dell'Almagesto. Al riguardo dobbiamo sottolineare che la precisione del catalogo di Tolomeo e del catalogo di Ulugbek è praticamente la stessa; pertanto, è possibile che i loro cataloghi furono effettivamente compilati nello stesso periodo.
2. Il catalogo di Tycho Brahe.
2.1. La caratteristica generale del catalogo di Tycho Brahe e il risultato della nostra datazione.
L'edizione del catalogo di Tycho Brahe che abbiamo scelto per la ricerca, originariamente era di Keplero e risale al 1628; è stata successivamente ristampata in [1024]. In questa edizione il catalogo di Tycho Brahe è stato fatto risalire al 1600 d.C. per mezzo della precessione longitudinale. La struttura del catalogo coincide con quella dell'Almagesto, come pure l'ordine in cui le costellazioni sono state elencate, ad eccezione di diverse costellazioni proprio alla fine del catalogo dell'Almagesto, che non sono presenti nell'opera di Tycho Brahe. Ci sono complessivamente 1005 stelle nel catalogo di Tycho Brahe. Il principio di costruzione degli strumenti usati da Tycho Brahe è lo stesso di quelli descritti da Tolomeo. Pertanto, nonostante i numerosi miglioramenti e il fatto che la procedura di fabbricazione dello strumento sia molto più evoluta, il livello di precisione di Tycho Brahe è paragonabile a quello del catalogo dell'Almagesto, forse un pochino meglio. È pari a 2'-3' contro i 10'-15' dell'Almagesto. Il drastico salto nelle osservazioni astronomiche sembra che abbia avuto luogo un po' più tardi, dopo l'invenzione del telescopio.
Si presume che la datazione delle osservazioni di Tycho Brahe sia conosciuta molto bene, vale a dire il 1570-1600. La datazione del catalogo di Tycho indipendente dalla cronologia consensuale, utilizzando come dati solo le coordinate stellari contenute nel catalogo, ci offre l'opportunità di testare il metodo di datazione che suggeriamo di utilizzare per l'esempio di un problema la cui soluzione è nota a priori. L'intervallo di datazione risultante è il seguente: 1510 - 1620 d.C. Ha una lunghezza di 110 anni e copre l'intervallo temporale delle osservazioni di Tycho Brahe. Facciamo notare che la lunghezza di questo intervallo è di circa 6 volte inferiore a quella che abbiamo ottenuto per l'Almagesto (circa 700 anni) usando lo stesso metodo. Il motivo è che il livello di precisione delle osservazione di Tycho Brahe è di circa 5-6 volte superiore a quello di Tolomeo.
2.2. L'analisi degli errori latitudinali di Tycho Brahe e la rimozione dei “refusi”.
Nella nostra datazione del catalogo di Tycho Brahe abbiamo di nuovo usato solo le latitudini stellari e le ragioni sono le stesse dell'Almagesto. L'identificazione delle stelle del catalogo di Tycho Brahe sulla moderna sfera celeste è stata presa dal lavoro di Bailey ([1024]).
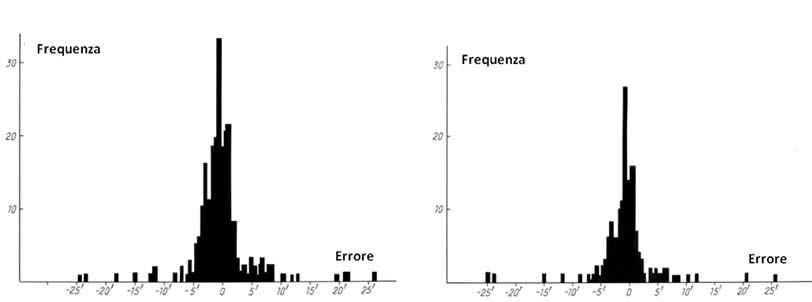
Si presume che Tycho Brahe abbia osservato circa solo 800 stelle delle 1005 incluse nel suo catalogo ([65], pagina 126). Se fosse davvero così, i dati contenuti nel suo catalogo non sarebbero di natura omogenea. Al fine di determinare quale parte del catalogo di Tycho Brahe è omogenea, abbiamo costruito degli istogrammi per la frequenza dell'errore latitudinale per ciascuna delle aree celesti A, Zod A, B, Zod B, C, D ed M. Vedere le Figure 9.1 - 9.7 per i risultati.
Tenete a mente che le aree celesti in questione sono già state definite in precedenza, durante la nostra analisi dell'Almagesto (vedere il paragrafo 3 del Capitolo 2). Per poter costruire questi istogrammi abbiamo calcolato le coordinate dell'eclittica stellare per l'epoca del 1600 d.C. Dopodiché abbiamo confrontato le latitudini delle stelle prese dal catalogo di Tycho Brahe con le rispettive latitudini stellari che abbiamo calcolato. Nelle Figure 9.1 - 9.7 la scala del tasso di errore è stata divisa in segmenti di 0,5' ciascuno. Questa scala è orizzontale. In quella verticale troverete la frequenza di manifestazione di un certo tasso di errore.
L'istogramma della discrepanza latitudinale
per la regione celeste A del catalogo di Tycho Brahe, con t = 3.
L'istogramma della discrepanza latitudinale
per la regione celeste Zod A del catalogo di Tycho Brahe, con t = 3.
L'istogramma della discrepanza latitudinale
per la regione celeste B del catalogo di Tycho Brahe, con t = 3.
L'istogramma della discrepanza latitudinale
per la regione celeste Zod B del catalogo di Tycho Brahe, con t = 3.
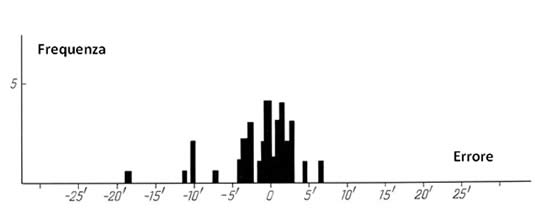
Figura 9.5.
L'istogramma della discrepanza latitudinale per la regione celeste C del catalogo di Tycho Brahe, con t = 3.

L'istogramma della discrepanza latitudinale
per la regione celeste D del catalogo di Tycho Brahe, con t = 3.
L'istogramma della discrepanza latitudinale
per la regione celeste M del catalogo di Tycho Brahe, con t = 3.
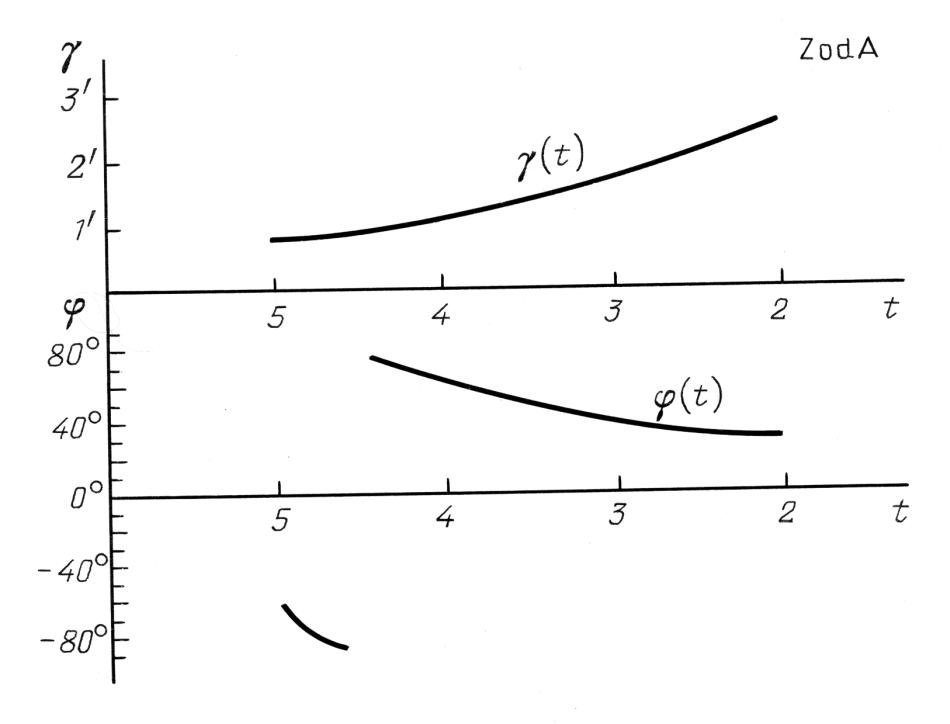
Figura 9.9.
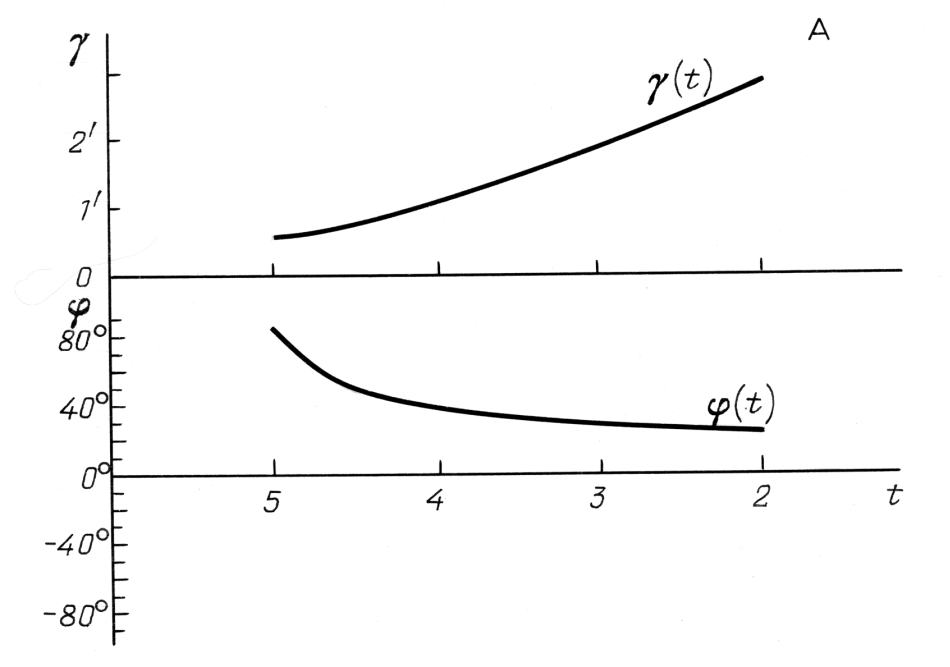
I grafici di γstat(t) e φstat(t) per la regione celeste Zod A
nel catalogo di Tycho Brahe.
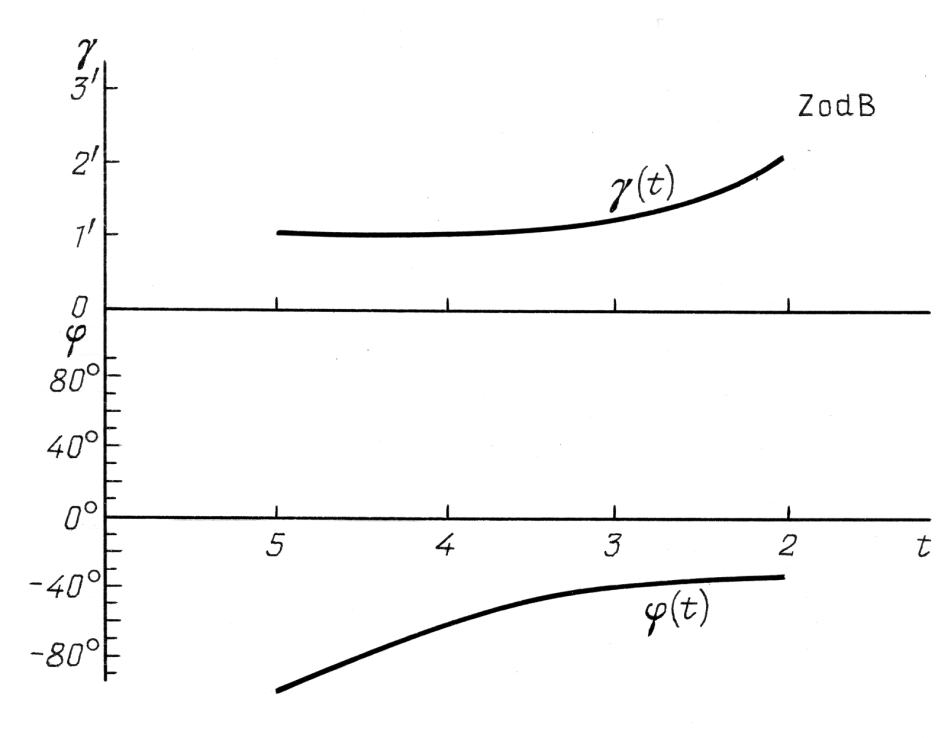
Figura 9.11.
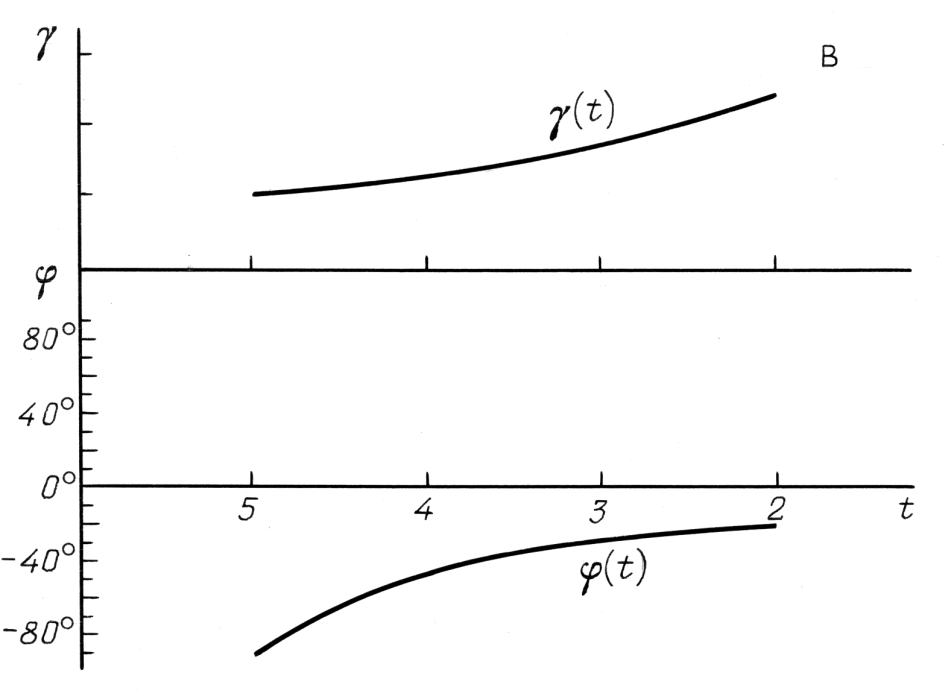
I grafici di γstat(t) e φstat(t) per la regione celeste Zod B
nel catalogo di Tycho Brahe.

Figura 9.14.
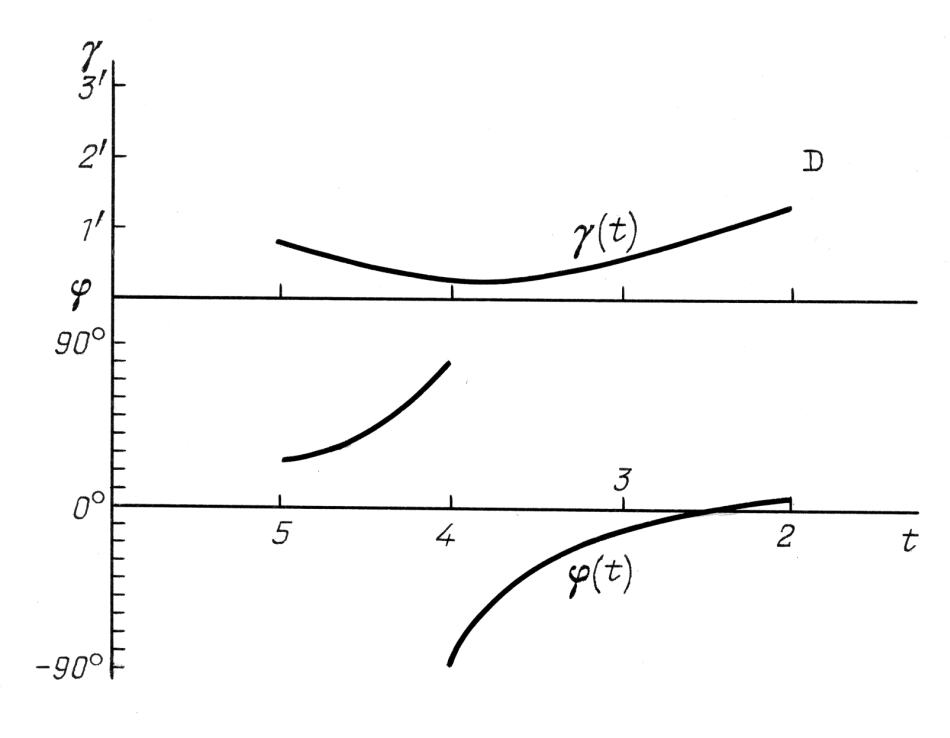
. I grafici di γstat(t) e φstat(t) per la regione celeste M
nel catalogo di Tycho Brahe.
I risultanti istogrammi dimostrano che tra gli errori latitudinali nelle coordinate del catalogo di Tycho Brahe troviamo infatti dei refusi. Se dovessimo presumere che gli errori nelle misurazioni delle coordinate stellari siano distribuiti normalmente, che sarebbe un'aspettativa giustificata, scopriremmo che circa il 15% dei valori degli errori sono situati al di fuori dell'intervallo 3σ. Questi valori sono dei “refusi”. Inoltre, abbiamo notato che gli istogrammi sono spostati verso lo zero. Il valore approssimativo di questo spostamento equivale a 2' e ci dice che il catalogo di Tycho Brahe contiene un errore sistematico nella latitudine stellare con parametro γ ≈ 2'. Tenete a mente che i valori γ e φ, che parametrizzano l'errore sistematico del catalogo, sono stati introdotti nel Capitolo 5.
Le stelle che abbiamo escluso dal catalogo di Tycho Brahe durante la filtrazione dei refusi, sono quelle il cui errore latitudinale non rientra nella distribuzione normale. Ciò è stato fatto singolarmente per ciascuna delle aree celesti A, B, C, D e M. Più precisamente, abbiamo escluso le stelle delle aree A, B e M, il cui valore di discrepanza latitudinale era superiore a 5' o inferiore a –7'. Tutte le stelle con un valore assoluto di discrepanza latitudinale maggiore di 5' sono state escluse dall'area C, così come tutte le stelle dell'area D con una discrepanza superiore a 4' o inferiore a –3'. A giudicare dalle Figure 9.1 - 9.7, i confini dell'errore indicati sono stati stimati approssimativamente. Abbiamo escluso un totale di 187 stelle su 1005. La quantità delle stelle rimanenti (818) è vicina a 777, che è la quantità di stelle osservate dallo stesso Tycho Brahe secondo la leggenda (vedi [65],pagina 126).
Dopo la “filtrazione dei refusi” descritta sopra dal catalogo di Tycho Brahe, parametri γstat(t) e φstat(t) dell'errore sistematico sono stati calcolati per la parte restante del catalogo come funzioni della presunta datazione t. Vedere il Capitolo 5 per le rispettive definizioni. L'intervallo di alterazione t scelto, inizia con il 1400 d.C., ovvero t = 5 e termina con il 1700 d.C. ossia t = 2.
Il risultato del calcolo delle funzioni di γstat(t) e φstat(t) per ciascuna delle sette regioni celesti (vedere il paragrafo 2 del Capitolo 6) è stato rappresentato graficamente nelle Figure 9.8 - 9.14. I grafici dimostrano chiaramente che il parametro φ assume dei valori sostanzialmente differenti per le diverse aree celesti del catalogo di Tycho Brahe e non sembra che rappresenti un errore sistematico. D'altro canto, il parametro γ si comporta esattamente allo stesso modo per ogni regione celeste.
A proposito, abbiamo osservato una situazione simile durante l'analisi del catalogo dell'Almagesto, vedere il Capitolo 6. I grafici di γstat(t) per le regioni celesti A, Zod A, B, Zod B, C e M del catalogo di Tycho Brahe si assomigliano l'un l'altro, vedere le Figure 9.8 - 9.14. L'area celeste D è l'unica eccezione; in questa regione il parametro γ si comporta diversamente, vedere la Figura 9.13. Pertanto, nella nostra datazione delle osservazioni di Tycho Brahe abbiamo escluso le stelle della regione celeste D.
2.3. La scelta del kernel informativo per il catalogo di Tycho Brahe.
Seguendo l'algoritmo da noi suggerito per la datazione delle osservazioni astronomiche, dobbiamo scegliere il kernel informativo per il catalogo di Tycho Brahe. Come è già stato sottolineato in [643] (vedere il paragrafo 8 dell'Introduzione di [643]), Tycho Brahe scelse una base di 21 stelle in vicinanza dello zodiaco, dopo aver stimato le loro coordinate equatoriali con la massima precisione possibile. Dopodiché, le convertì in coordinate dell'eclittica. L'elenco di queste stelle è stato preso in prestito da [1049] (vedere Tabella 9.1).
| Tabella 9.1. Le stelle di base del catalogo di Tycho Brahe. | ||||||||
|
Le stelle di base dal catalogo di Tycho Brahe | α1900,ore, minuti e secondi | β1900,ore, minuti e secondi | Tasso annuale di moto proprio, in secondi d’arco | l = longitudine dell’eclittica | b = latitudine dell’eclittica | Valore | |
| Vα | Vδ | |||||||
| Secondo il catalogo moderno ([1197]) | Secondo il catalogo di Tycho Brahe ([1024]) | |||||||
| 1 | 5 γ Ari | 1.48.02,4 | +18°48’21” | +0.079 | -0.108 | Ari 27°37.0’ | +7°08.5’ | 4 |
| 2 | 13 α Ari | 2.01.32,0 | +22°59'23" | +0.190 | -0.144 | Tau 2°06.0' | +9°57.0' | 3 |
| 3 | 74 ε Tau | 4.22.46,5 | +18°57'31" | +0.108 | -0.036 | Gem 2°53.0' | –2°36.5' | 3 |
| 4 | 87 α Tau | 4.30.10,9 | +16°18'30" | +0.065 | -0.189 | Gem 4°12.5' | –5°31.0' | 1 |
| 5 | 13 μ Gem | 6.16.54,6 | +22°33'54" | +0.055 | -0.112 | Gem 29°44.0' | –0°53.0' | 3 |
| 6 | 24 γ Gem | 6.31.56,1 | +16°29'05" | +0.043 | -0.044 | Can 3°31.0' | –6°48.5' | 2 |
| 7 | 78 β Gem | 7.39.11,8 | +28°16'04" | -0.627 | -0.051 | Can 17°43.0' | +6°38.0' | 2 |
| 8 | 43 γ Can | 8.37.29,9 | +21°49'42" | -0.103 | -0.043 | Leo 1°57.0' | +3°08.0' | 4 |
| 9 | 41 γ Leo | 10.14.27,6 | +20°20'51" | +0.307 | -0.151 | Leo 23°59.0' | +8°47.0' | 2 |
| 10 | 32 α Leo | 10.03.02,8 | +12°27'22" | -0.249 | -0.003 | Leo 24°17.0' | +0°26.5' | 1 |
| 11 | 29 γ Vir | 12.36.35,5 | –0°54'03" | -0.568 | -0.008 | Lib 4°35.5' | +2°50.0' | 3 |
| 12 | 67 α Vir | 13.19.55,4 | –10°38'22" | -0.043 | -0.033 | Lib 18°16.0' | –1°59.0' | 1 |
| 13 | 27 β Lib | 15.11.37,4 | –9°00'50" | -0.098 | -0.023 | Vir 13°48.0' | +8°35.0' | 2 |
| 14 | 1 δ Oph | 16.19.06,2 | –3°26'13" | -0.048 | -0.145 | Vir 26°44.5' | +17°19.0' | 3 |
| 15 | 21 α Sco | 16.23.16,4 | –26°13'26" | -0.007 | -0.023 | Sag 4°13.0 | –4°27.0' | 1 |
| 16 | 39 o Sag | 18.58.41,4 | –21°53'17" | +0.079 | -0.060 | Cap 9°28.0' | +0°59.0' | 4 |
| 17 | 53 α Aqi | 19.45.54,2 | +8°36'15" | +0.537 | +0.385 | Cap 26°09.0' | +29°21.5' | 2 |
| 18 | 40 γ Capr | 21.34.33,1 | –17°06'51" | +0.188 | -0.022 | Aqu 16°14.0' | –2°26.0' | 3 |
| 19 | 22 β Aqu | 21.26.17,7 | –6°00'40" | +0.019 | -0.005 | Aqu 17°51.0' | +8°42.0' | 3 |
| 20 | 54 α Peg | 22.59.46,7 | +14°40'02" | +0.062 | -0.038 | Pis 17°56.5' | +19°26.0' | 2 |
| 113 α Pis | 1.56.52,3 | +2°16’51” | +0.062 | -0.038 | Ari 23°47.5’ | -9°04.5’ | 3 | |
Per le costellazioni che contengono stelle da questo elenco abbiamo trovato gli errori di gruppo γstatG(t) e φstatG(t) per t = 3. Vedere il paragrafo 3 del Capitolo 6 per le definizioni di questi valori. Le stelle delle costellazioni per le quali l'errore di gruppo γstatG(t) differiva da γstatZodA(t) per più di 2' per t = 3, sono state escluse da ulteriori considerazioni. Per le restanti costellazioni abbiamo calcolato la percentuale di stelle il cui errore latitudinale non superava rispettivamente 1', 2' e 3' per t = 3. Quindi abbiamo calcolato la discrepanza latitudinale media quadratica per ogni costellazione, ignorando e considerando l'errore sistematico con i parametri γstatG(t) e φstatG(t) per t = 3. Gli stessi parametri sono stati calcolati dopo la compensazione del comune errore sistematico con i parametri γstatZodA (3) = 1.8', φ=0. Abbiamo scoperto che la compensazione degli errori sistematici comuni ci ha portato allo stesso risultato della compensazione dell'errore di gruppo per ciascuna delle costellazioni considerate, vedere la Tabella 9.2. Ora possiamo considerare che l'errore sistematico sia stato comune per il gruppo delle costellazioni che abbiamo studiato e che usano i valori di γstatZodA (t), φ=0.
Nel kernel informativo del catalogo di Tycho Brahe abbiamo incluso 12 stelle delle 21, quelle che sono rimaste nel catalogo dopo la “filtrazione degli errori di gruppo” descritta sopra. A parte questo, abbiamo incluso al suo interno due stelle veloci e luminose con nome: Arturo = α Boo e Procione = α CMi. La terza stella veloce con nome (Sirio) non è stata inclusa nel kernel informativo, dal momento che si trova nella regione celeste D che possiede un singolo errore sistematico, vedi sopra. Pertanto, il kernel informativo del catalogo di Tycho Brahe è composto da 14 stelle:
γ Ari, α Ari = Hamal, ε Tau, α Tau = Aldebaran,γ Can = Aselli, γ Leo, α Leo = Regolo, γ Vir, α Vir = Spiga, Δ Oph, α Aqu, α Pis, α Boo = Arturo e α CMi = Procione.
2.4. La datazione delle osservazioni di Tycho Brahe.
Come si evince dalla Tabella 9.2, l'errore latitudinale medio quadratico residuale dopo la compensazione del complesso sistematico con i parametri γstatZodA (t), φ=0 fluttua entro i limiti di 1' - 3' per le costellazioni che contengono le stelle del kernel informativo. La percentuale di stelle nelle costellazioni il cui errore latitudinale è inferiore a 2', è più grande del 50% in tutti i casi.
Secondo l'intervallo di datazione suggerito nel Capitolo 7, occorre prendere 2' come soglia Δ. Quindi si dovrebbe determinare l'intervallo temporale per il quale la discrepanza latitudinale di tutte le stelle del kernel informativo non supera Δ = 2'. L'intervallo risultante conterrà le possibili datazioni delle osservazioni di Tycho Brahe.
Abbiamo calcolato questo intervallo temporale. Comincia nel 1510 d.C. e termina nel 1620 d.C. (2,8 ≤ t ≤ 3,9). Per il catalogo di Tycho Brahe abbiamo usato una misura di 10 anni. Come in precedenza, la presunta datazione del catalogo t è misurata in secoli e contata a ritroso dal 1900.
Il comportamento dell'errore latitudinale massimo perle stelle del kernel informativo con t che varia da 2.6 a 4.2 ,è illustrato da una serie di disegni simili alla Figura 7.10 che illustra l'esempio dell'Almagesto (vedere la Figura 9.15).
L'area dei parametri (γ, φ) con un marcato colore nero, ha un errore latitudinale massimo di 2'. L'area con un'ombreggiatura regolare ha un errore massimo di 2,5'. La Figura 9.15 dimostra che la crescita del livello della soglia di 2,5' espande il possibile intervallo di datazione al 1490-1640 d.C. e non di più (al posto del precedente 1510-1620 d.C.) Se scegliessimo il livello Δ =3', avremmo un possibile intervallo di datazione del 1480-1620 d.C.
Pertanto, come nel caso del catalogo dell'Almagesto, i confini del possibile intervallo di datazione per il catalogo di Tycho Brahe dipendono solo marginalmente dal livello di variazione Δ.
Ulteriori calcoli hanno dimostrato che anche l'intervallo di datazione delle osservazioni di Tycho Brahe è stabile in caso di variazione del contingente del kernel informativo.
2.5. Conclusioni.
- Il nostro metodo applicato al catalogo di Tycho Brahe produce un possibile intervallo di datazione di 110 anni (tra il 1510 e il 1601 d.C.) L'intervallo risultante copre la vita di Tycho Brahe (1546-1601). Il periodo delle osservazioni di Tycho Brahe nell'osservatorio di Uraniborg (1576-1597) si colloca in mezzo a questo periodo, intorno al 1565.
- Il possibile intervallo di datazione per le osservazioni di Tycho Brahe dimostra un buon livello di stabilità con variazioni del livello Δ e variazioni nel contingente del kernel informativo. Alzando il livello Δ da 2' a 3' questo intervallo cresce di 200 anni (1480-1680 d.C.)
- Il possibile intervallo di datazione risultante è pari a 110 anni ed è circa 6 volte più corto di quello calcolato per l'Almagesto (700 anni). Questo corrisponde al fatto che il catalogo di Tycho Brahe è 5 - 6 volte più preciso dell'Almagesto, vale a dire che ha una soglia di errore di 2' - 3' rispetto a 10' - 15'.
- Il possibile intervallo di datazione statistica per il catalogo di Tycho Brahe è correlato all'intervallo geometrico per i livelli di confidenza di 1 - ε > 0.9.
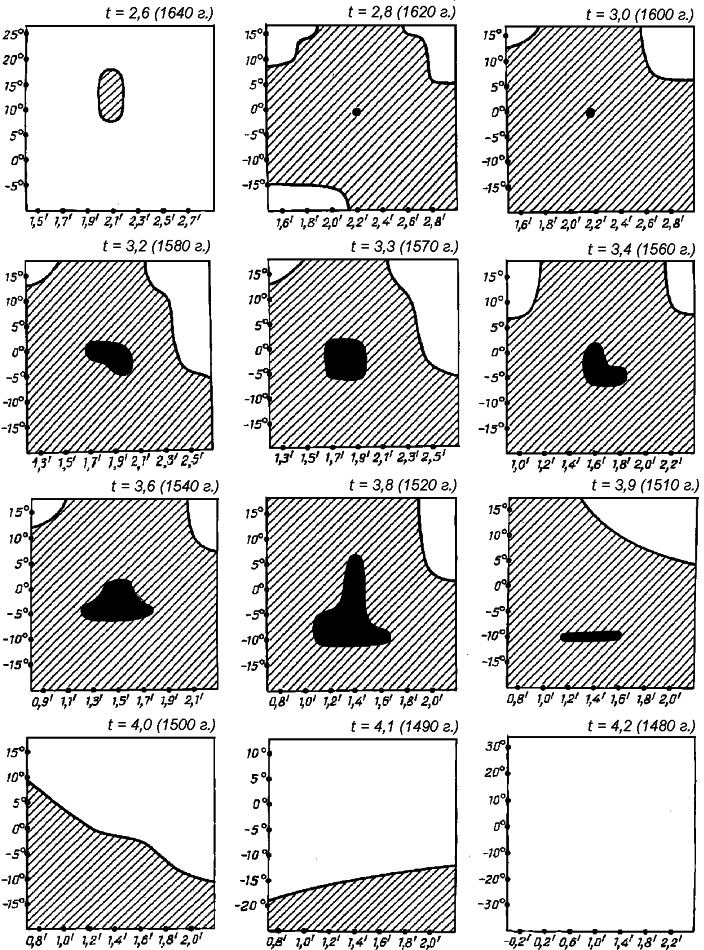
Figura 9.15.
La discrepanza latitudinale massima Δ(t, γ, φ) del catalogo di Tycho Brahe per valori di t compresi tra 2,6 e 4,2, ovvero dal 1480 d.C. al 1640 d.C. L'area con Δ non maggiore di 2' è colorata di nero; l'area con Δ non maggiore di 2'30" ha un'ombreggiatura regolare.
| Tabella 9.2. I risultati dei calcoli per il catalogo di Tycho Brahe. | |||||
| Costellazione. Numero di stelle in una costellazione | Rotazione della sfera celeste | La percentuale di stelle in una costellazione il cui tasso di errore latitudinale non supera il valore di: | Discrepanza media quadratica residuale | ||
| 1’ | 2’ | 3’ | |||
| Cancro, 13 stelle | -(condizione prima della rotazione) | 38 | 77 | 77 | 2.40’ |
| ottimale per Zod A | 61 | 85 | 92 | 2.37’ | |
| ottimale per costellazione | 61 | 77 | 92 | 2.37’ | |
| γ=γstatZodA (t), φ=0 | 46 | 77 | 92 | 2.37’ | |
| Leone, 36 stelle | -(condizione prima della rotazione) | 61 | 83 | 94 | 1.41’ |
| ottimale per Zod A | 55 | 80 | 94 | 1.44’ | |
| ottimale per costellazione | 61 | 83 | 94 | 1.35’ | |
| γ=γstatZodA (t), φ=0 | 47 | 75 | 94 | 1.63’ | |
| Toro, 37 stelle | -(condizione prima della rotazione) | 76 | 89 | 94 | 1.18’ |
| ottimale per Zod A | 54 | 92 | 97 | 1.31’ | |
| ottimale per costellazione | 67 | 92 | 94 | 1.17’ | |
| γ=γstatZodA (t), φ=0 | 24 | 62 | 94 | 1.94’ | |
| Pesci, 31 stelle | -(condizione prima della rotazione) | 61 | 77 | 90 | 1.81’ |
| ottimale per Zod A | 48 | 81 | 90 | 1.97’ | |
| ottimale per costellazione | 64 | 81 | 90 | 1.79’ | |
| γ=γstatZodA (t), φ=0 | 45 | 77 | 87 | 1.87’ | |
| Acquario, 34 stelle | -(condizione prima della rotazione) | 29 | 56 | 76 | 2.49’ |
| ottimale per Zod A | 32 | 59 | 82 | 2.23’ | |
| ottimale per costellazione | 35 | 82 | 91 | 1.63’ | |
| γ=γstatZodA (t), φ=0 | 38 | 65 | 91 | 1.90’ | |
| Vergine, 32 stelle | -(condizione prima della rotazione) | 25 | 72 | 94 | 1.80’ |
| ottimale per Zod A | 34 | 72 | 94 | 1.83’ | |
| ottimale per costellazione | 62 | 91 | 100 | 1.16’ | |
| γ=γstatZodA (t), φ=0 | 59 | 91 | 94 | 1.22’ | |
| Ariete, 20 stelle | -(condizione prima della rotazione) | 65 | 85 | 100 | 1.22’ |
| ottimale per Zod A | 60 | 40 | 100 | 1.21’ | |
| ottimale per costellazione | 50 | 95 | 100 | 1.20’ | |
| γ=γstatZodA (t), φ=0 | 45 | 65 | 90 | 1.63’ | |
| Ofiuco, 24 stelle | -(condizione prima della rotazione) | 17 | 37 | 70 | 2.84’ |
| ottimale per Zod A | 46 | 79 | 92 | 1.93’ | |
| ottimale per costellazione | 50 | 92 | 92 | 1.69’ | |
| γ=γstatZodA (t), φ=0; | 25 | 54 | 83 | 2.40’ | |
3. Il catalogo di Ulugbek.
3.1. La caratteristica generale del catalogo di Ulugbek e il risultato della nostra datazione.

Figura 9.15a.
Il frontespizio del catalogo di Ulugbek
Si presume che il catalogo di Ulugbek sia una versione molto precisa del catalogo stellare dell'Almagesto, basata sulle osservazioni astronomiche eseguite nell'osservatorio di Samarcanda a metà del XV secolo d.C., durante il regno di re Ulugbek ([1339]). Tuttavia, secondo Peters e Knobel, “sebbene Ulugbek abbia di fatto compilato un catalogo più preciso di quello di Tolomeo, la sua opera non è mai stata ampiamente utilizzata” ([1339], pagina 7). Uno studio sul catalogo di Ulugbek dimostra che si tratta di fatto del catalogo stellare tolemaico. In entrambi i cataloghi, non solo coincide il contingente stellare, ma anche l'ordine delle stelle elencate, le cui eccezioni sono poche e distanti tra loro. Ci sono 1019 stelle nel catalogo di Ulugbek. I valori delle coordinate dell'eclittica sono dati al minuto, ma la precisione effettiva di questo catalogo è sostanzialmente inferiore.
Alcuni ricercatori l'hanno stimata pari a 3' - 5' (vedere [65]). Tuttavia, i nostri calcoli dimostrano per il catalogo di Ulugbek una dispersione residua dell'errore latitudinale pari a 16,5' per l'area celeste Zod A, che è dove abbiamo riscontrato la massima precisione. Per cui, la precisione latitudinale effettiva del catalogo di Ulugbek è di circa 30' - 35', che è di gran lunga molto inferiore a quella dell'Almagesto!
D'altra parte, l'errore sistematico γ è più piccolo nel catalogo di Ulugbek rispetto che all'Almagesto. Di conseguenza, la precisione latitudinale del primo nella sua forma iniziale, ovvero prima dell'esclusione dell'errore sistematico, è in qualche modo superiore alla precisione latitudinale nel testo originale del catalogo dell'Almagesto. La differenza è uguale a 5' - 6'. Tuttavia, questa differenza è piuttosto inconsistente rispetto al tasso di errore (latitudinale) in entrambi i cataloghi presi nella loro forma iniziale, senza la compensazione dell'errore sistematico. Non sorprende che il catalogo di Ulugbek non abbia mai preso il posto dell'Almagesto nei circoli scientifici. Nella Figura 9.15a riportiamo il frontespizio del catalogo di Ulugbek.
L'istogramma del tasso di errore latitudinale del catalogo di Ulugbek per le stelle dell'area celeste A, è visibile nella Figura 9.16. Prima della costruzione dell'istogramma sono state escluse dalla considerazione tutte le stelle la cui discrepanza latitudinale ha superato 1 grado per t = 5, ossia il 1400 d.C.
I nostri calcoli dimostrano anche che il catalogo di Ulugbek contiene dei palesi furti dall'Almagesto (e viceversa). Nella Figura 9.17 possiamo vedere l'istogramma della differenza tra le latitudini stellari del catalogo di Ulugbek e le rispettive latitudini stellari nell'Almagesto. L'identificazione delle stelle di Ulugbek con le loro controparti dell'Almagesto non ha presentato problemi poiché, come è già stato sottolineato, l'ordine delle stelle coincide per entrambi i cataloghi.
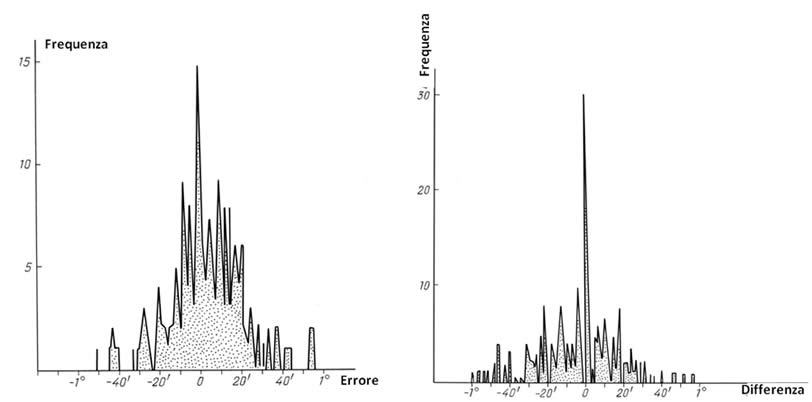
L'istogramma della discrepanza latitudinale per l'area celeste Zod A
nel catalogo di Ulugbek, con t = 5.
L'istogramma della differenza di frequenza per le latitudini stellari
del catalogo di Ulugbek e dell'Almagesto,
senza la compensazione dell'errore sistematico
(Ulugbek - Almagesto).
Il brusco picco a zero nella Figura 9.17 corrisponde al gruppo di stelle le cui latitudini coincidono completamente in entrambi i cataloghi. Questo picco è abbastanza grande da non lasciare spazio a speculazioni sul fatto che possa essere casuale.
3.2. L’errore sistematico nel catalogo di Ulugbek.
I parametri dell'errore sistematico γstat(t) e φstat(t) sono stati calcolati per la regione celeste Zod A dal catalogo di Ulugbek, con le presunte datazioni che vanno dal 100 a.C. al 1800 d.C. (1 ≤ t ≤ 20). Vedere il paragrafo 2 del Capitolo 6 per maggiori dettagli riguardanti il calcolo di γstat(t) e φstat(t) ). I risultati dei calcoli di γstat(t) e φstat(t) per le tre datazioni presunte del 1500 d.C. (t = 4), 900 d.C. (t = 10) e 400 d.C. (t = 15) sono stati compilati nella Tabella 9.3, che è dove abbiamo anche trovato i valori dell'errore medio quadratico prima e dopo la compensazione dell'errore sistematico con i parametri γ = γstate φ = φstat.
3.3. La scelta del kernel informativo e la soglia Δ. La datazione del catalogo di Ulugbek.
Proprio come abbiamo fatto per la datazione del catalogo dell'Almagesto, compiliamo il kernel informativo del catalogo di Ulugbek usando le stelle con nome dell'area A e delle sue immediate vicinanze, in quanto sono la parte del cielo più attentamente osservata. Arriveremo alla fine con le stesse 9 stelle con nome dell'area A che abbiamo trovato nell'Almagesto, vale a dire:
Arturo = α Boo, Regolo = α Leo, Spiga = α Vir, Antares = α Sco, Capella = α Aur, Lira = Vega = α Lyr, Aselli = α Can, Procione = α CMi e Previndemiatrix = ε Vir.
Questa volta non escludiamo dalla considerazione la stella Previndemiatrix come abbiamo fatto per l'Almagesto, dal momento che le sue coordinate nel catalogo di Ulugbek non sono il risultato di calcoli successivi e quindi pare che non contengano errori da parte dello scriba ([1024]).
Secondo la Tabella 9.3, come valore della soglia di precisione Δ per le latitudini delle stelle con nome dell'area celeste A scegliamo 10', come abbiamo fatto per l'Almagesto. Infatti, dopo la compensazione dell'errore sistematico la discrepanza latitudinale media quadratica per l'area celeste Zod A è uguale a 16.5'. Dopo la compensazione dell'errore sistematico, il 45% delle stelle di quest'area ha un errore latitudinale residuale massimo di 10'.
| Tabella 9.3. Il catalogo di Ulugbek. I risultati dei calcoli di γstat (t), φstat (t) per le tre datazioni presunte del 1500 d.C., 900 d.C. e 400 d.C. |
||||
| Date | γstat | φstat | σinit | σmin |
| t = 4, ossia 1500 d.C. | 11.55 | -43° | 18.36 | 16.43 |
| t = 10, ossia 900 d.C. | 10.33 | -60° | 17.92 | 16.33 |
| t = 15, ossia 400 d.C. | 10.87 | -76° | 18.1 | 16.35 |
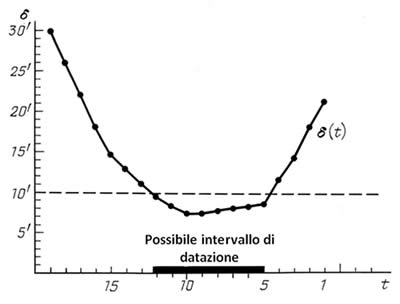
Figura 9.18.
Il grafico della discrepanza minima di Δ(t) per le stelle del kernel informativo
del catalogo di Ulugbek che dipendono dalla presunta datazione t.
Dopo aver selezionato il kernel informativo del catalogo e aver definito la soglia Δ di 10', otteniamo un intervallo geometrico di possibili datazioni per il catalogo di Ulugbek, vale a dire il 700 d.C. - 1450 d.C. L'intervallo statistico delle possibili datazioni coincide con quello geometrico per un livello di fiducia superiore a 0,4. Il risultante intervallo di datazione del catalogo di Ulugbek rimane stabile quando cambia il livello di Δ, come pure in caso di variazione del contingente del kernel informativo. Quindi, per Δ = 15' questo intervallo si espande al 400 d.C. - 1600 d.C.
Il grafico della discrepanza latitudinale minima Δ(t) per le stelle del kernel informativo, è stato costruito nella Figura 9.18 come una funzione della presunta datazione t. Questo grafico è simile a quello che si può vedere nella Figura 7.27 calcolato per il catalogo dell'Almagesto. Tenete a mente che Δ(t) è il minimo tra tutti i metodi possibili per far corrispondere la configurazione stellare del kernel informativo del catalogo di Ulugbek con quella effettiva (calcolata) per il momento t dell'errore latitudinale massimo che coinvolge tutte le stelle del kernel informativo. È ovvio che se si dovesse risolvere il metodo della sovrapposizione reciproca delle due combinazioni stellari, si potrebbe calcolare la discrepanza latitudinale singolarmente per ogni stella e quindi prendere il valore massimo di questo errore per tutte le stelle della configurazione. Nello specifico, la Figura 9.18 dimostra le possibili variazioni dell'intervallo di datazione del catalogo di Ulugbek, risultanti dalla variazione del livello Δ. Il confronto della Figura 9.18 con la Figura 7.27 conferma la circostanza che abbiamo sottolineato in precedenza, vale a dire il fatto che sia le caratteristiche di precisione delle coordinate del catalogo dell'Almagesto che quelle del catalogo di Ulugbek sono simili le une alle altre.
3.4. Conclusioni.
- Il possibile intervallo di datazione geometrico per il catalogo di Ulugbek inizia nel 700 d.C. e finisce nel 1450 d.C. Copre la datazione scaligeriana della creazione del catalogo, che è il 1437 d.C., sebbene abbiamo fatto notare che questa datazione verrà spostata verso la fine dell'intervallo calcolato. D'altra parte, questo intervallo è notevolmente simile a quello a cui siamo arrivati per l'Almagesto: dal 600 d.C. al 1300 d.C. È quindi possibile che entrambi i cataloghi siano stati compilati nello stesso momento.
- Le caratteristiche di precisione dei cataloghi di Ulugbek e Tolomeo praticamente coincidono. La componente sistematica dell'errore latitudinale è maggiore nell'Almagesto rispetto che al catalogo di Ulugbek: circa 20' anziché 10'. D'altro canto, il composto casuale residuo per l'area celeste Zod A è in qualche modo più grande nel catalogo di Ulugbek, ovvero, = 16.5' invece che 12.8'. È stato anche scoperto che le coordinate delle 48 stelle presenti in entrambi i cataloghi coincidono completamente, e la cosa è causata dal fatto che un catalogo ha rubacchiato i dati dall'altro.
- Il possibile intervallo di datazione del catalogo di Ulugbek è stabile alle variazioni del livello Δ e alle variazioni del contingente del kernel informativo.
- Il possibile intervallo di datazione statistico per il catalogo di Ulugbek coincide con l'intervallo geometrico per qualsiasi livello di confidenza 1 - ε > 0.4. Se alzassimo la soglia Δ a 15', il corrispondente intervallo statistico per 1 - ε ≤ 0,999 si ridurrebbe a circa 100 anni di distanza dal limite superiore, arrivando al 1500 d.C. anziché il 1600 d.C.
4. Il catalogo di Hevelius.
4.1. La dipendenza tra il catalogo di Tycho Brahe e quello di Hevelius.
Il catalogo di Hevelius è stato compilato nella seconda metà del XVII secolo, già dopo l'invenzione del telescopio. Tuttavia, Hevelius fu riluttante ad usare il telescopio e pensava che le sue osservazioni ad occhio nudo fossero più precise ([1024]). Questo venne confermato da Galley dopo una sorta di “competizione” con Hevelius mentre stavano osservando le coordinate delle stesse stelle usando metodi differenti: il telescopio per Galley e i tradizionali strumenti astronomici per Hevelius. I risultati differirono solo per 1" ([1024]). Gli scritti delle epoche successive furono del parere che nelle sue osservazioni Hevelius fu preciso tanto quanto gli astronomi che usavano i telescopi (con un tasso di precisione di 1 secondo). Nel catalogo di Hevelius le coordinate stellari sono riportate in secondi d'arco.
La nostra analisi non conferma questo punto di vista popolare. Abbiamo studiato diverse configurazioni che comprendono le stelle luminose con nome del catalogo di Hevelius, tra i quali c'erano tre stelle veloci: Arturo = α Boo, Sirio = α CMa e Procione = α CMi. Per rappresentare la presunta datazione delle osservazioni di Hevelius, sono stati scelti i valori di t nell'intervallo 1 ≤ t ≤ 5, ossia il 1400 d.C. - 1800 d.C. Inoltre, quello che abbiamo cercato di trovare ogni volta era la sovrapposizione della configurazione stellare del catalogo di Hevelius sulla rispettiva configurazione stellare effettiva (calcolata) per il momento temporale t, per il quale la discrepanza latitudinale massima per la configurazione stellare sarebbe la più bassa possibile. Come al solito, con “latitudini” noi intendiamo dire le latitudini dell'eclittica delle stelle.
Abbiamo scoperto che sono i parametri di rotazione della sfera celeste che definiscono questa sovrapposizione ottimale come pari a zero (γ = 0, φ = 0). L'implicazione è che le configurazioni stellari del catalogo di Hevelius che abbiamo studiato non contengono errori sistematici, oppure che secondo Hevelius nelle coordinate non c'è alcuno spostamento attraverso la sfera celeste, che renderebbe l'errore sistematico uguale a zero. Tuttavia, gli errori latitudinali casuali hanno lo stesso tasso medio come quelli contenuti nel catalogo di Tycho Brahe, vale a dire, 2' - 3'. Tutto questo considerando che il valore del grado della scala nel catalogo di Hevelius è di 60 volte più piccolo di quello del catalogo di Tycho Brahe: 1" invece di 1'. E' venuto fuori che gli errori latitudinali prodotti da Hevelius sono di 100 - 200 volte più grandi del valore del grado della sua scala numerica!
Questa circostanza è stata illustrata nella Figura 9.19. Contiene i grafici dell'errore latitudinale come funzioni della presunta datazione t per ciascuna delle 10 stelle luminose con nome del catalogo di Hevelius:
Arturo = α Boo, Sirio = α CMa, Procione = α CMi, Antares = α Sco, Vega = Lira = α Lyr, Polluce =β Gem, Castore = α Gem, Spiga = α Vir, Capella = α Aur e Regolo = α Leo.
Nella Figura 9.20 possiamo vedere lo stesso grafico creato per il catalogo di Tycho Brahe. Il confronto delle due figura dimostra che l'errore latitudinale è lo stesso per entrambi i cataloghi. Inoltre, i valori dell'errore effettivo per alcune delle stelle contenute nei cataloghi di Tycho Brahe ed Hevelius sono vicini l'uno all'altro. Questo vale per Arturo, Sirio, Antares, Procione e Lira = Vega. Si tratta di una chiara indicazione di dipendenza tra i cataloghi di Tycho Brahe ed Hevelius.
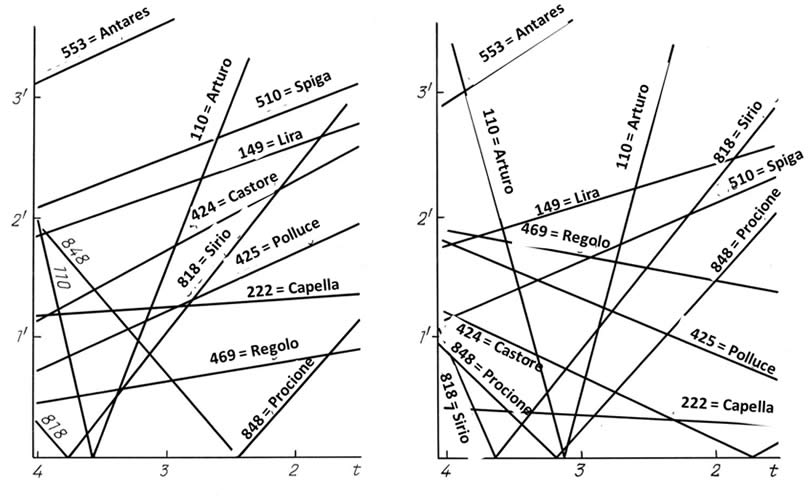
Gli errori latitudinali nel catalogo di Hevelius.
Gli errori latitudinali nel catalogo di Tycho Brahe.
4.2. Conclusioni.
- La precisione del catalogo di Hevelius non è per niente superiore a quella del catalogo di Tycho Brahe. Questa osservazione è il risultato dell'analisi delle configurazioni di stelle luminose e con nome presenti nel catalogo di Hevelius.
- A quanto pare, il catalogo di Hevelius è dipendente dal catalogo di Tycho Brahe. Ovviamente, questa dipendenza è evidente per il gruppo di stelle luminose e veloci, vale a dire Arturo, Sirio e Procione. Siccome le stelle veloci con nome formano la base per la datazione dei vecchi cataloghi stellari, la datazione indipendente dei cataloghi di Hevelius non ha alcun senso. Il risultato sarà vicino a quello che abbiamo ottenuto per il catalogo di Tycho Brahe.
5. Il catalogo di Al-Sufi.
Abbiamo preso in prestito il catalogo stellare di Al-Sufi da [1394]. Di solito si presume che il catalogo di Al-Sufi sia stato compilato da lui stesso tramite le sue stesse osservazioni ([516]). L'autore si oppone a quegli astronomi che quando compilano dei cataloghi con il loro nome, usano le cosmosfere e i cataloghi pronti all'uso come l'Almagesto al posto che eseguire le osservazione effettive delle stelle.
Ci dice quanto segue:
“Ho visto molti di coloro che si battono per la conoscenza delle stelle immobili ... e ho scoperto che fanno parte di due categorie persone. La prima categoria segue il metodo degli astronomi e usa le cosmosfere dipinte da artisti che non conoscono le stelle e usano le longitudini e le latitudini che trovano nei libri per segnare la posizione delle stelle sulla sfera, incapaci di separare la verità dall’errore. In seguito ho conosciuto persone che studiano le sfere e vedono che le stelle disegnate sopra differiscono da quelle osservate in cielo. I creatori di cosmosfere fanno riferimento alle tavole astronomiche i cui autori affermano di aver osservato le stelle e stimato loro stessi le posizioni. In realtà, hanno semplicemente scelto le stelle più famose, quelle conosciute da tutti come l’Occhio del Toro, il Cuore del Leone [Regolo – l’autore], l’Orecchio della Vergine del Grano [Spiga – l’autore], le tre stelle sulla fronte dello Scorpione e il cuore di quest’ultimo [Antares – l’autore], le stesse stelle le cui longitudini e latitudini Tolomeo dice di aver osservato e incluso nell’Almagesto, poiché tutte queste stelle sono vicine all’eclittica. Come per le altre stelle che Tolomeo indica nel suo catalogo stellare, aggiungono qualsiasi valore suggerisca la loro immaginazione. Dopo aver spostato queste stelle nello spazio per il valore dell'intervallo tra il proprio periodo di vita e quello di Tolomeo, aggiungono o sottraggono alcuni minuti alle longitudini di Tolomeo, per dar l'impressione che le osservazioni siano state condotte da loro e che dal processo siano scaturite alcune differenze nelle longitudini e nelle latitudini, a prescindere dagli incrementi stellari generali o dalla quantità di tempo che li separa da Tolomeo. Tutto ciò è stato fatto senza alcuna vera conoscenza delle stelle. Coloro sono Al-Batani, Atarid e altri. Ho studiato attentamente molte copie dell'Almagesto e ho scoperto che differiscono dalla moltitudine delle stelle immobili. La seconda categoria di persone che cerca la conoscenza delle stelle immobili è composta da dilettanti”. Citazione da [544], Volume 4, pagine 239-241.
Tuttavia, il confronto delle coordinate stellari del catalogo dell'Almagesto e di quello di Al-Sufi rende ovvio che il catalogo di Al-Sufi non è altro che una delle numerose versioni esistenti dell'Almagesto.
Infatti, l'ordine in cui sono elencate le stelle nel catalogo dell'Almagesto e in quello di Al-Sufi, è esattamente lo stesso. Le longitudini di tutte le stelle fornite da Al-Sufi sono state aumentate tramite uno spostamento di 12° 42' rispetto alla versione canonica del catalogo dell'Almagesto ([1339]), mentre le latitudini sono esattamente le stesse. Facciamo notare che lo spostamento delle longitudini tramite una singola costante o farle appartenere a un'altra epoca storica attraverso la precessione, è davvero presente anche in alcune copie scritte a mano e stampate dell'Almagesto, per esempio il manoscritto 11 dalla copia citata in [1339]. Il cosiddetto “Codice Veneziano 312” contiene latitudini stellari più grandi di 17 gradi rispetto a quelle di Tolomeo ([1339], pagina 20).
Peters e Knobel commentano come segue: “Si può vedere che le vere [secondo Peters e Knobel - l'autore] longitudini di Tolomeo, così come la varietà modificata, hanno sostituito le cifre originali” ([1339]), pagina 20. In un modo o nell'altro, ciò che abbiamo trovato qui si può qualificare con le tracce di certe “attività” che coinvolgono il catalogo dell'Almagesto. Possiamo vedere che per qualche motivo le longitudini del catalogo dell'Almagesto sono state spostate in varie epoche storiche. I successivi editori dell'Almagesto potevano aver avuto inizialmente delle opinioni diverse sul motivo esatto dello spostamento longitudinale del catalogo e successivamente furono d'accordo nel scegliere proprio l'epoca dell'alba della nuova era. Studiare in modo critico le copie sopravvissute dell'Almagesto sotto questa luce, potrebbe essere davvero di valore per la nostra ricerca.
Inoltre, è venuto fuori che nel manoscritto latino dell'Almagesto, la datazione del presunto 1490 d.C. si trasformò nel modo seguente: “Osservando la precessione, lo scriba aggiunse [al catalogo stellare - l'autore] le longitudinali stellari per l'epoca da Adamo, dopo averle impostate al 3496 a.C. ed aver spostato quelle longitudini alla metà del XV secolo d.C.” ([1017]: 1), inserito tra le pagine 128 e 129. Pertanto, gli storici pro Scaligero potrebbero datare l'Almagesto all'epoca antidiluviana di Adamo, commettendo un errore davvero madornale.
Possiamo vedere un altro spostamento della precisione longitudinale del catalogo dell'Almagesto nell'epoca del XVI secolo d.C., nell'edizione latina dell'Almagesto che risale al 1537 (conservata a Colonia; potete leggere di più al riguardo nel Capitolo 11).
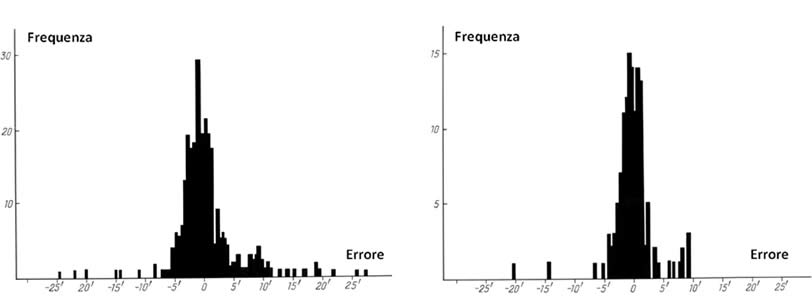
Il confronto delle latitudini di tutte le stelle contenute nel catalogo di Al-Sufi ([1394]) con quelle nella versione canonica dell'Almagesto, dimostra che solo 53 stelle su 1028 mostrano delle differenze di latitudine: un tasso molto tipico per le diverse copie dell'Almagesto. Inoltre, le latitudini per 35 di queste 53 stelle di Al-Sufi coincidono con le versioni delle latitudini contenute nelle copie dell'Almagesto studiate da Peters e Knobel ([1339]). Pertanto, il catalogo di Al-Sufi è semplicemente una copia del catalogo dell'Almagesto (dobbiamo sottolineare che questa conclusione è stata fatta anche dall'astronomo J. Evans ([1119] e [1120]), il cui approccio era del tutto diverso).
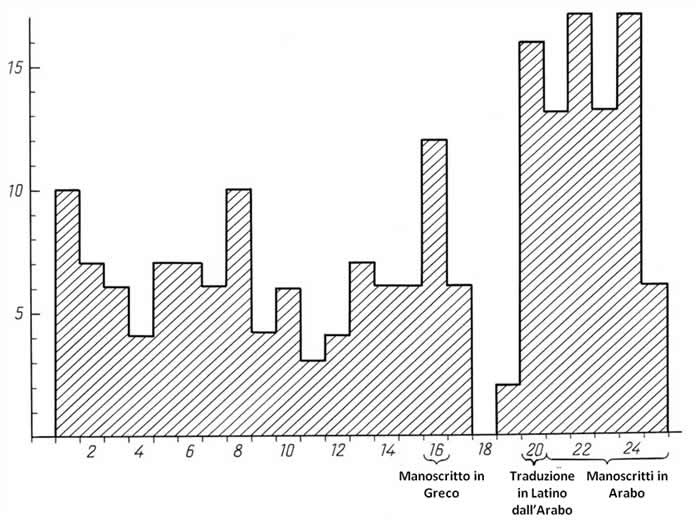
Figura 9.21.
Il grafico contiene le seguenti indicazioni per ciascuno dei 25 manoscritti dell'Almagesto: il numero di casi per cui la discrepanza tra le latitudini specificate da Al-Sufi e quelle nella versione canonica dell'Almagesto è uguale a quella del manoscritto in esame.
Nella Figura 9.21 si può vedere un diagramma che indica tutti i casi in cui le latitudini che nel catalogo di Al-Sufi differiscono da quelle della versione canonica dell'Almagesto, coincidono con quelle contenuti in uno dei 25 manoscritti dell'Almagesto studiati da Peters e Knobel in [1339]. Il gruppo delle copie scritte a mano dell'Almagesto che assomiglia molto al catalogo di Al-Sufi, nella Figura 9.21 è numerato da 20 a 24. È interessante notare che questo gruppo è costituito dai manoscritti arabi che discendevano dallo stesso prototipo: la cosiddetta “traduzione di Al-Mamon”, ovvero la traduzione dell'Almagesto che si presume sia stata realizzata da Al-Mamon nel IX secolo d.C.(vedi [1339], pagina 23). A quanto pare, il catalogo di Al-Sufi contenuto in [1394] deve essere attribuito allo stesso gruppo di copie dell'Almagesto.
Riportiamo la conclusione fatta da Peters e Knobel: “La traduzione francese di Skjellerup dal catalogo arabo di Abd Al-Rahman Al-Sufi, è solo una versione del catalogo di Tolomeo spostata in un'epoca diversa” ([1339], pagina 7).
Tuttavia, gli storici continuano ad affermare che per qualche motivo bizzarro il catalogo di Al-Sufi è di natura indipendente e basato proprio sulle osservazioni di Al-Sufi, per il quale i venerabili studiosi di storia dichiarano che “abbia perseguito l'obiettivo di verificare i cataloghi stellari di Tolomeo e degli astronomi d'Oriente, correggendoli secondo i dati empirici della sua osservazione” ([515], pagina 190).
Per cui, siamo stati testimoni del fatto che il catalogo stellare dell'Almagesto sia stato fatto risalire a numerose “epoche desiderate” da diversi astronomi che usavano il metodo longitudinale della precessione, aggiungendo o sottraendo un valore costante. Potrebbero averlo fatto per una varietà di motivi. Il catalogo risultante veniva attribuito a un altro astronomo, Al-Sufi per esempio. In altri casi, il nome e la paternità di Tolomeo furono mantenuti intatti, ma lo stesso “antico” Tolomeo viaggiò indietro nel tempo e giunse da qualche parte intorno all'inizio della nuova era, a causa della “prova indiscutibile” presentata dalle longitudini del suo catalogo. che divennero magicamente “antiche” per mezzo di una semplice operazione aritmetica.